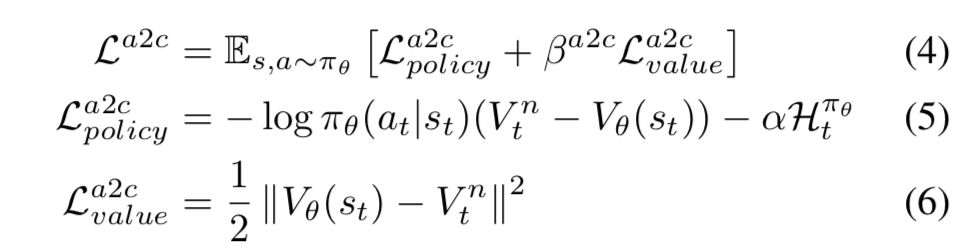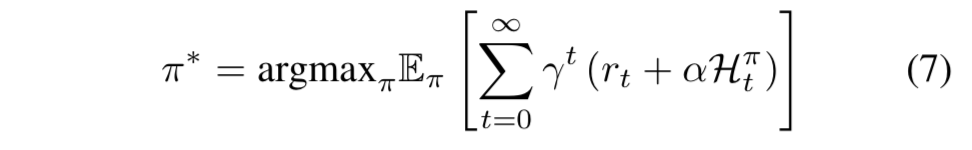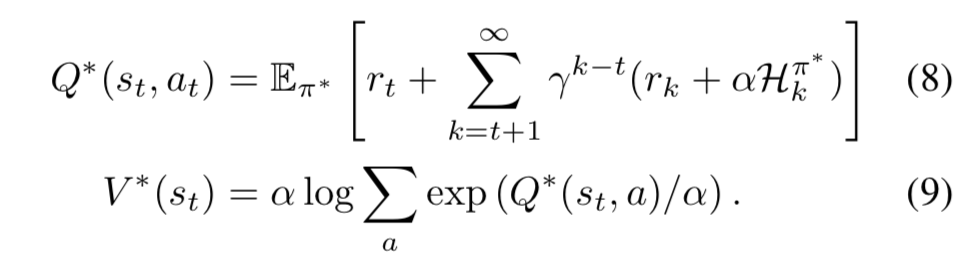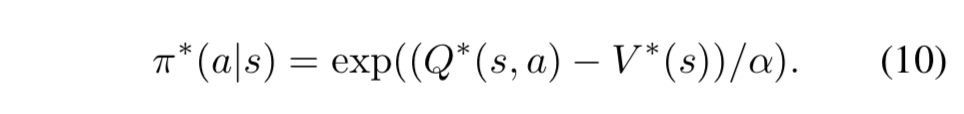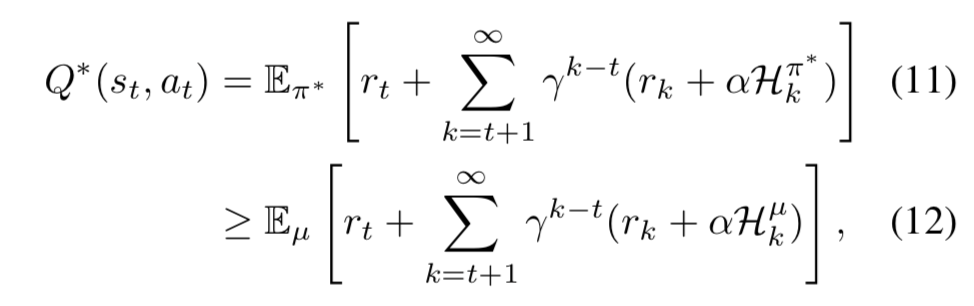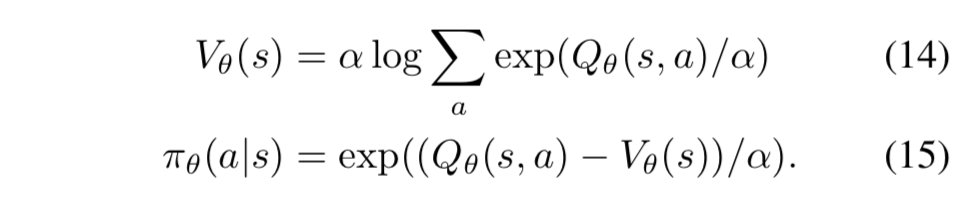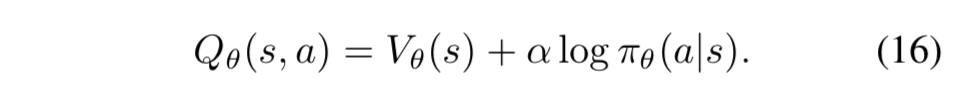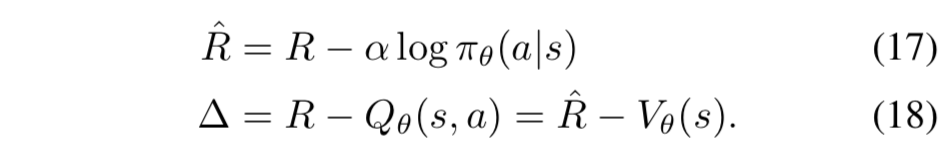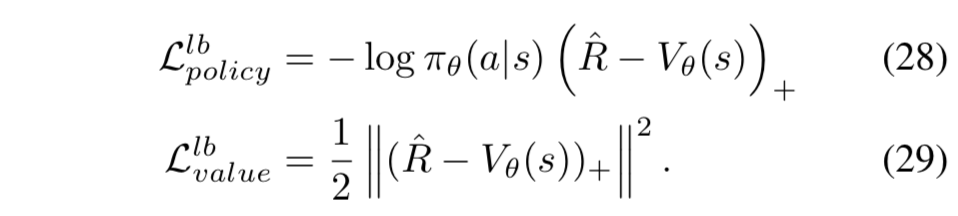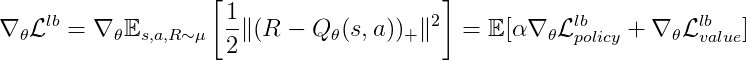More than 5 years have passed since last update.

【論文】Self-Imitation Learning (SIL, 2018)

Posted at 2018-07-27

[1806.05635] Self-Imitation Learning

メタ情報

Google Brain
ICML2018 (Oral)
- PFN の藤田さんと同じセッション (https://icml.cc/Conferences/2018/Schedule?showParentSession=3482)

概要

自己模倣学習；Self-Imitation Learning (SIL) を提案する
- 過去の良かった決断を再現するような、シンプルな方策オフ型の actor-critic アルゴリズム
過去の良い経験を再現することは、間接的に深い探索につながるのではという仮定

導入

(略)

自己模倣学習；Self-Imitation Learning

過去の良かった経験を利用するため、経験再生バッファを採用して、次の方策オフ型 actor-critic ロスを考える：
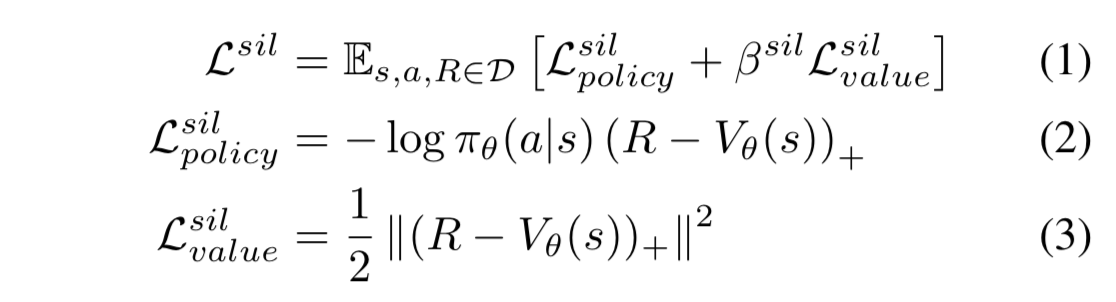
- $\pi$ が方策 (すなわち actor) で、 $V$ が価値関数 (すなわち critic)
- $( \cdot )_+ = \max(\cdot, 0)$ 、つまり、 $R > V$ のとき (=得られた報酬が自分の推定よりも大きい時) しか更新が発生しない
- (2) 式が、 $V$ をベースラインとした方策勾配
  - ただし $R$ に方策オンの収益ではなく、方策オフのモンテカルロ収益を採用
  - サンプルウェイトが $R-V$ であるようなクロスエントロピーロスと見ることもできる ¹
- (3) 式が収益Rに関する方策オフ推定ロス

優先度付き経験再生

理論上は、リプレイバッファはどんな方策からのサンプルでも良い
$R > V$ となるサンプル数の効率向上のため、 $(R-V_\theta(s))_+$ を優先度として経験再生をおこなう

Advantage Actor-Critic with SIL (A2C+SIL)

オリジナルの A2C のロスは：
A2C+SIL では、方策オン型の $L^{a2c}$ による更新と、M回の $L^{sil}$ による更新を両方実施

理論的正当性

主張

SIL の目的関数 $L^{sil}$ ((1) 式) は、
エントロピー正則化強化学習 (entropy-regularized RL) における
下界ソフトQ学習 (lower-bound-soft-Q-learning) の実装とみなすことができる

エントロピー正則化強化学習；Entropy-Regularized RL

エントロピー正則化強化学習の目的は、γ割引報酬和と方策のエントロピーの和を最大化する確率的方策を学習することである：
- 直感的には、高いエントロピー (＝行動がひとつに決めづらい) の状態を推奨するということになる
最適ソフトQ関数と最適ソフト価値関数を次のように定義する：
すると、(7) 式は次の通りになることが証明されている：

下界ソフトQ学習；Lower Bound Soft Q-Learning

最適ソフトQ関数の下界

任意の挙動方策 $\mu$ による期待収益は、最適ソフトQ関数の下界となる (最適性から明らか)：

下界ソフトQ学習

下界ソフトQ学習の目的関数を次のように提案する：
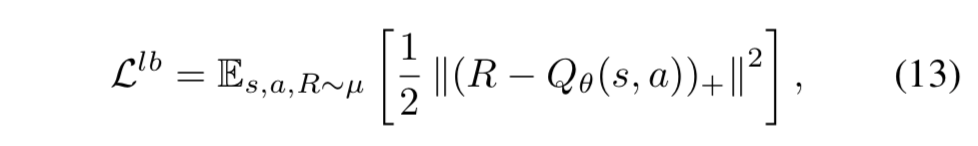
- この式は、 $Q^*(s,a) \geq R > Q_\theta(s,a)$ の関係から正当化される
  - もし $R \leq Q_\theta(s,a)$ なら、その状態行動ペアは最適ソフトQ関数に関する情報を持っていない ²

SIL と下界ソフトQ学習の繋がり

actor-critic における（13）式の等価表現と、それの SIL との繋がりを示す
(9), (10) 式のアナロジーから、価値関数と方策、行動価値関数を次のように考える：
- さらに、次を定義する：
- 以上を用いると次の式が得られる ³⁴
- これを (1)(2)(3) 式と見比べると、 $\mathcal{L}^{sil}$ が、下界ソフトQ学習 ((13) 式) の $\alpha \rightarrow 0$ バージョン、つまりエントロピーボーナス項を無視した形式であることがわかる
下界ソフトQ学習は、Q値を最適Q値の下界に向かって更新する手法なので、自己模倣学習は、方策 $\pi_\theta$ と価値関数 $V_\theta$ をそれぞれの最適値に向かって更新している

A2C と SIL の関係

A2C は、学習器の方策に関して収益を増加させるように方策を更新する
- 価値関数と方策の一貫性は方策オン型のサンプルを用いることで制約する
SIL は、方策と価値関数を直接的に最適なものへと更新する
- 方策オフ型のサンプルを用いる
エントロピー正則化 A2C は n-step ソフトQ学習とみなせることがわかっている
- つまり、エントロピー正則化 RL のもとでは、A2C も SIL も最適ソフトQ関数に関する学習をおこなっているということなので、双方を組み合わせることは相補的である

実験

Key-Door-Treasure 実験

格子状の環境における実験
カウントベースの探索ボーナスが入る手法 ("EXP") と SIL、およびその組み合わせ
実験結果からは、SIL とカウントベースの探索アルゴリズムは相補的であることが示唆された

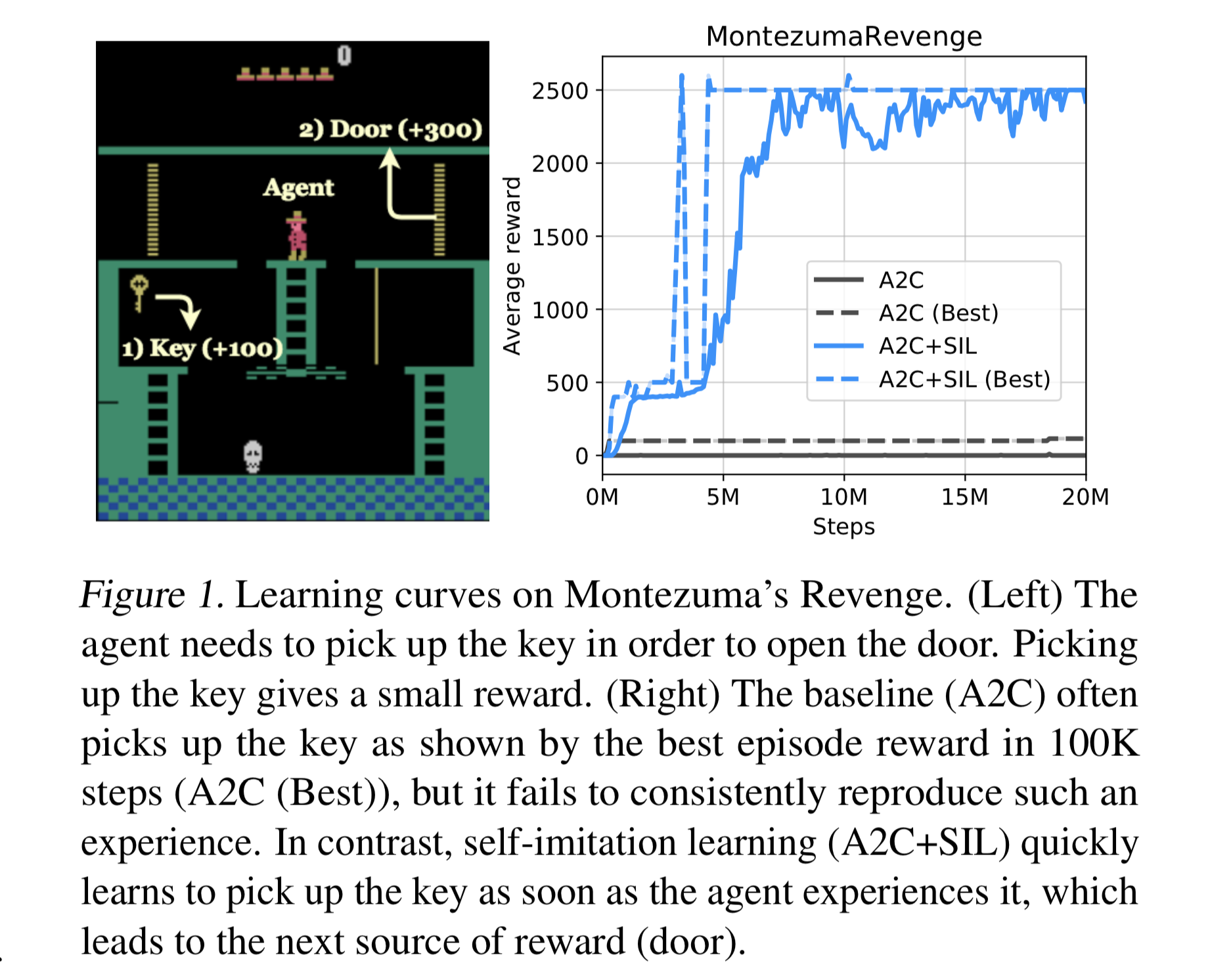
探索が困難な Atari ゲーム

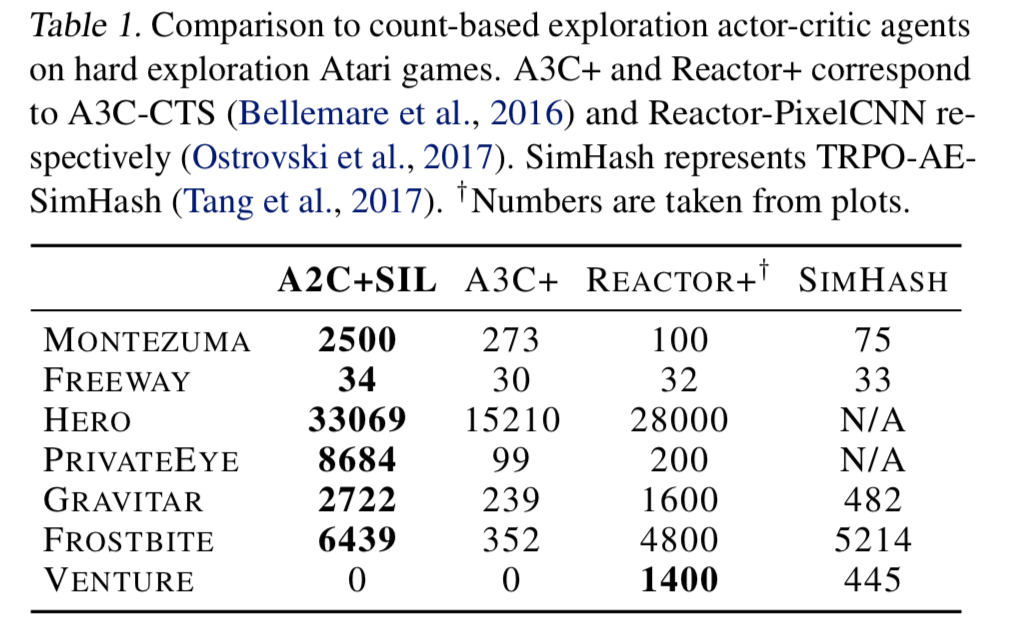
「過去の経験の活用は、より深い探索に役立つ」という主張を裏付けるような実験結果が得られたのではないだろうか
SIL には探索ボーナスが入っていないにも関わらず、探索が困難な Atari ゲームで良い成績を出している (Table 1)
- ただし、ランダム行動で一切報酬が入らない「Venture」では SIL は失敗している

Atari ゲーム全体でのパフォーマンス

SIL によって、探索が簡単なゲームから困難なゲームまで、全体的に性能向上
SIL は James Bond や Star Gunner といったゲームでは局所解に陥っている
- 自己模倣学習をおこなう回数であるハイパーパラメータを小さくすることでこの問題を回避できることはわかったが、パラメータの自動調整は将来の課題

下界ソフトQ学習の効果

A2C に単に優先度付き経験再生を導入した方法 (ACPER) だと性能が良くない
- ACER で提案された actor-critic の方策オフ型更新を利用
- 性能がいまいちなのは、過去の良い経験を生み出した方策と現在の方策が離れすぎていると、重点サンプリングによってそのサンプルの恩恵を失うからだと推測している
SIL で重点サンプリングがいらないのは、挙動方策に従ったサンプルから推定方策のパラメータ推定をしているわけではなく、最適ソフトQ関数の下界への直接更新であるからだ

MuJoCo での性能

連続行動空間での実験であり、SIL が (A2C だけでなく) PPO とも組み合わせることができるということを示す
- ただし PPO と SIL の目的関数の繋がりには強い理論的な背景がないことに注意
この実験は報酬が密であるため、SIL のメリットを確認するために、「遅延報酬」バージョンも実験した (Figure 5 下行)
- 毎ステップもらえるはずの報酬を20ステップごとにまとめてしまう、という設定
- このような状況 (報酬が疎に近い状況) では、想定通り、SIL によるパフォーマンスのブーストがかかるようになる

参考資料

感想

失敗した経験ばかりをメモリにためてもしょうがない (経験再生バッファ内の経験は多様性があってほしい) という意味では、curiosity driven の強化学習アプローチにも似ている気がする
SIL で重点サンプリングによる補正が必要ない理由、論文中で言及されているが、ちゃんと理解できていない
とても過学習しそうで怖い。過去サンプルを何度も再利用するのは危険な気がするが、安定性はどうなんだろうか？

実際に取った行動 $a$ でのみ値が更新されることを考えれば、分類問題のクラス推定のときのクロスエントロピーロスと同じ形になっている ↩
ここの議論の正当化の話は理解できているかだいぶ怪しい。「 $Q^*(s,a) \geq R$ は明らか。もしも $R \leq Q_\theta(s,a)$ だったら、 $Q^*(s,a)$ と $Q_\theta(s,a)$ の大小関係が確定せず、更新に必要な情報が得られない。よって、更新をしたいのならば、 $R > Q_\theta(s,a)$ の場合のみを考えれば良い」くらいの意味だろうか？自信がない ↩
論文中の (19) - (27) 式で非常に丁寧な展開があるので、詳細はそちらをどうぞ ↩
この TeX が Qiita 上でレンダリングできない・・・なぜ・・・(本文中には画像化して貼った) \nabla_{\theta}\mathcal{L}^{lb} = \nabla_{\theta} \mathbb{E}_{s, a, R \sim \mu} \left[ \frac{1}{2} \lVert ( R - Q_\theta(s,a) )_+ \rVert ^2 \right] = \mathbb{E}[\alpha\nabla_\theta\mathcal{L}_{policy}^{lb} + \nabla_\theta\mathcal{L}_{value}^{lb}] ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

【論文】Self-Imitation Learning (SIL, 2018)

メタ情報

概要

導入

関連研究

探索

Episodic control

経験再生

actor-critic での経験再生

方策勾配法とQ学習の繋がり

不完全なデモンストレーションからの学習

自己模倣学習；Self-Imitation Learning

優先度付き経験再生

Advantage Actor-Critic with SIL (A2C+SIL)

理論的正当性

エントロピー正則化強化学習；Entropy-Regularized RL

下界ソフトQ学習；Lower Bound Soft Q-Learning

最適ソフトQ関数の下界

下界ソフトQ学習

SIL と下界ソフトQ学習の繋がり

A2C と SIL の関係

実験

Key-Door-Treasure 実験

探索が困難な Atari ゲーム

Atari ゲーム全体でのパフォーマンス

下界ソフトQ学習の効果

MuJoCo での性能

参考資料

感想