問題設定
正の整数 x と n があるとします。xをn等分してください。
xはnで割り切れるとは限りませんが、できるだけ均等にn分割したいです。
例えば、x=13, n=4 に対して (つまり13の4等分) は [3, 3, 3, 4] で、
割り切れる場合には、例えば x=15, n=3 に対してはもちろん [5, 5, 5] となります。
どうやったらこのn等分が求まるでしょうか?
結論
// を整数除算 (小数点以下を切り捨てる除算) とします。
求めたい等分リストlは、[(x+0)//n, (x+1)//n, ..., (x+(n-1))//n] です。
Python3で実装するなら、
x = 13
n = 4
l = [(x + i) // n for i in range(n)]
です。
議論とか
まずはじめに、この方法は有名な事実らしいです。
私が知らないだけで常識なのかもしれません。
整数のn分割はわりとよくやる処理なので、たまに書くことがありますが、いつも次のように実装していました:
x = 13
n = 4
# 同じ量を全員に配るとすると、もらえる量は
div = 13 // 4 # 13 // 4 = 3
# 同じ量を全員に配った後のあまりを求める
rem = 13 % 4 # 13 % 4 = 1
# n人中rem人は余りをひとつずつもらえる
l = [div] * (n - rem) + [div+1] * rem
計算効率的にはむしろ後者のほうが良いですが、綺麗じゃないといつも思っていたので、前者の綺麗な実装を見てちょっと感動したためわざわざ記事にしました。
ちなみに:前者の綺麗な実装がなぜ動くか?
x が n で割り切れる場合、x+0からx+(n-1)のnによる切り捨て除算はすべてx//nと同じ値となり、等分割ができます。
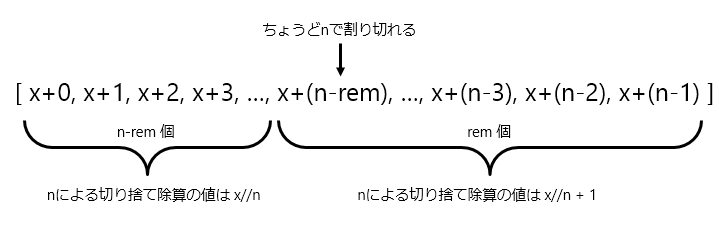
x が n で割り切れない場合は、その余りを rem とすると、x + (n-rem) は n で割り切れます。すると、x+0からx+(n-1)のリストのうち、x+(n-rem)から先はnによる切り捨て除算がすべてx//n + 1となります。 x+(n-rem),...,x+(n-1)のリストの長さはremですから、結局、他の人よりひとつずつ多くもらえるのは後ろから rem 個となります。
つまり、全員に均等に分けたあとにその余りを後ろからひとつずつ配っているのと同じことです。