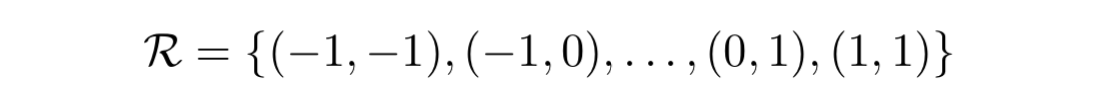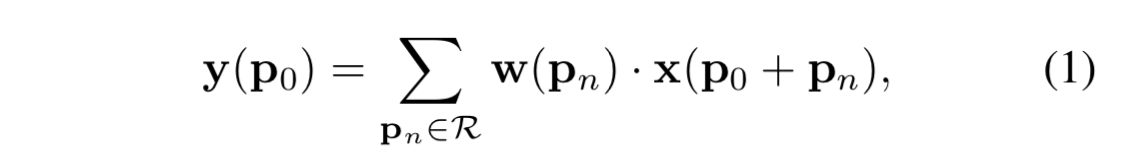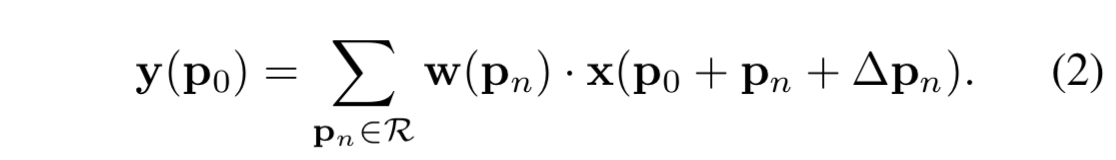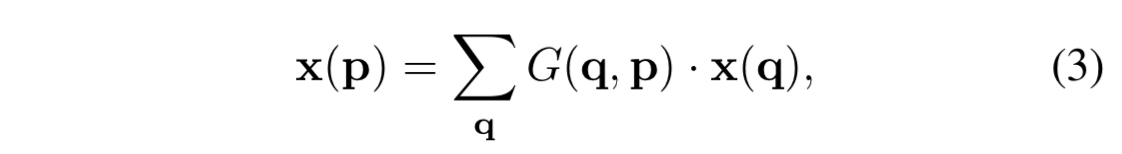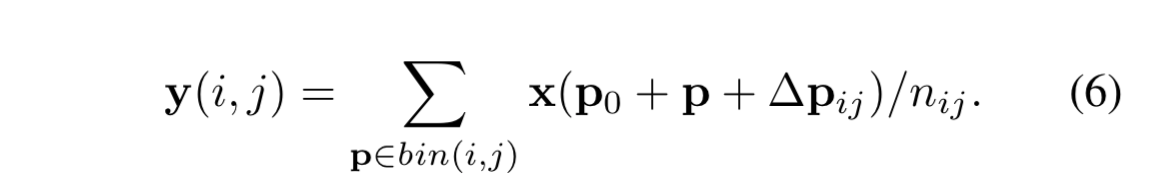[1703.06211] Deformable Convolutional Networks
メタ情報
- ICCV 2017 oral paper
- Microsoft Research Asia
- 著者実装
- 日本語による解説 (見つけられた範囲で)
概要
- 本質的に、CNN はその構造上、幾何的な 1 変換処理に制限されている
- その欠点を克服するために、 deformable convolution と deformable RoI pooling を提案する
- 物体検出と semantic segmentation のタスクで結果を検証する
導入
- 視覚認識タスクでのキーチャレンジは、物体のスケールやポーズ、視点、歪み等にどうやって対応するかだ。大きくふたつの方法があるが、それぞれに欠点もある：
- データ側の多様性を増やし (augmentation等で)、モデル側のキャパシティを十分大きくする
- 欠点：データが大規模になる。モデルが巨大になる。
- 変形に対して不変な特徴やアルゴリズム、例えば SIFT や max-pooling などを用いる
- 欠点：hand-crafted である
- データ側の多様性を増やし (augmentation等で)、モデル側のキャパシティを十分大きくする
- CNN は幾何的な構造を持つ ―― つまり、畳み込みも pooling も固定された位置に対する処理なので、幾何的な変形に対して弱い
- 例えば、CNN の同じ層では受容野の形と大きさが同じになるが、これは物体の意味論的な認識タスクではおかしい
- 他にも、物体認識で事前にバウンディングボックスを生成して特徴抽出するというのも明らかに最適なアルゴリズムではない
- そこで以下を提案する：
- 普通のグリッド型の畳み込みに学習可能な2Dオフセットを導入する deformable convolution
- RoI pooling のビン位置に学習可能なオフセットを導入する deformable RoI pooling
Deformable Convolutional Networks
Deformable Convolution
- 2D conv は次の2ステップからなる：
- 普通のグリッド $\mathcal{R}$ を使って入力からデータを切り出す
- 切り出したデータと重み $\boldsymbol{w}$ の内積を取る
- $\mathcal{R}$ が受容野のサイズとダイレーションを決めている。例えば、 3x3 dilation 1 のカーネルは：
- 普通の畳み込みでは、座標 $\boldsymbol{p}_0$ の出力値は次のような式で書ける：
- deformable convolution では、データ位置ごとのオフセット $\Delta\boldsymbol{p}$ を使って、次のようになる：
- これは入力データのサンプリングをグリッド状ではなく不規則におこなうということである
- $\Delta\boldsymbol{p}$ は一般には整数とは限らないので、(2) 式の x(・) の引数も整数ではなくなってしまうから、データは bilinear で補完する (q が p の周辺の整数座標2、G が補完の関数)：
- オフセットも学習対象である
- 具体的には、やろうとしている deformable conv と同じ特徴マップに畳み込みをした結果をオフセットとして利用する (つまり、「そのピクセルを中心とした deformable conv のオフセットはどれだけ？」という問題の答えを同じ特徴マップから畳み込みで出力している)。
- offset field の大きさは、入力特徴マップと同じ大きさとなる 3。また、チャネル数の 2N は、カーネルサイズの N に対応している。4
Deformable RoI Pooling
RoI pooling のビン処理にも、deformable なオフセットを同じように導入するという話。
普通の RoI pooling の話と、 Position-Sensitive (PS) RoI pooling の話がある。
普通の RoI pooling の場合
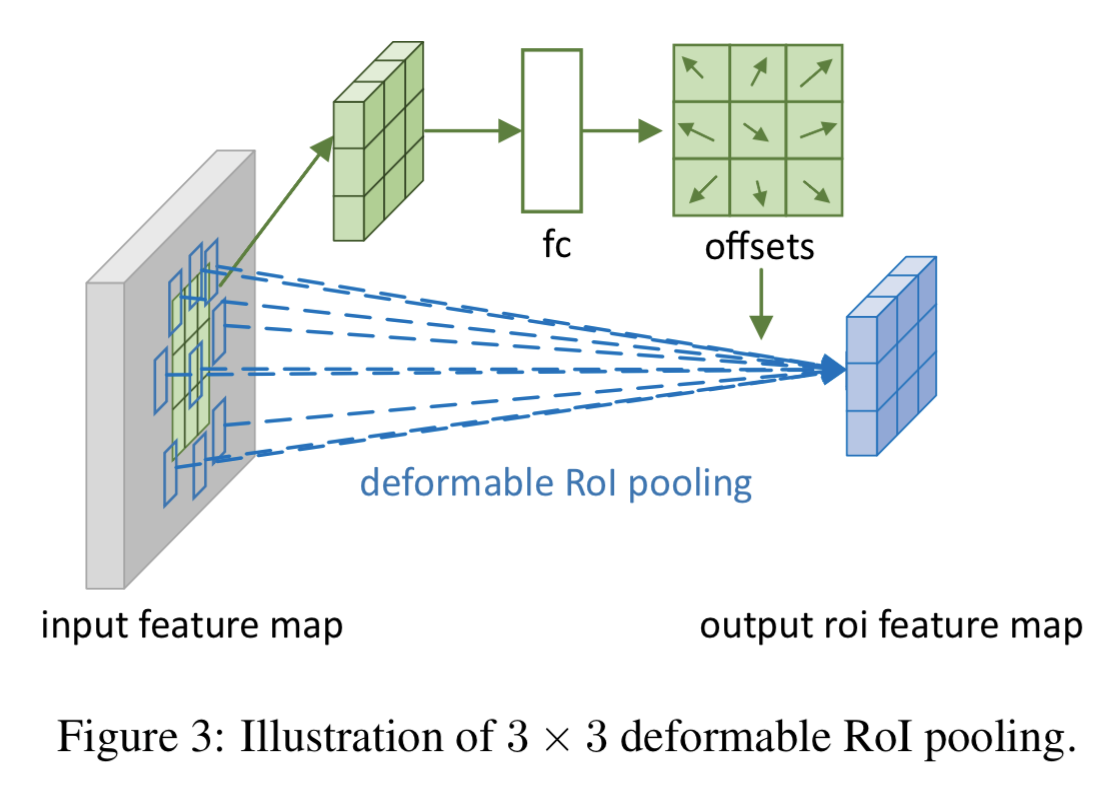
- この図が何を意味しているのかよくわからなかったが、「RoI pooling を掛けた結果に対して全結合層で offset field を計算。その offset を使って、再度入力特徴マップに対して RoI pooling をする」と言ってると思う (私の理解が誤っていなければ)。
- 式 (6) を計算するためには $\Delta\boldsymbol{p}$ が必要なのだが、それを計算するには $\Delta\widehat{\boldsymbol{p}}$ が必要 (
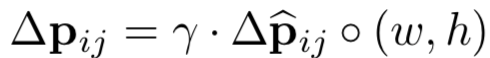) で、その $\Delta\widehat{\boldsymbol{p}}$ とは RoI pooling の結果に対して全結合層を適用したもののこと。
PS RoI Pooling の場合
- この図もけっこう曲者だが、やっていることは同じで、「PS RoI Pooling の "pooling" の処理の部分だけにうまく offset がかかるように offset field を作って、それを使って deformable pooling する」と言っていると思う (私の理解が誤っていなければ)。
- ただし、本文中にも注意があるように、元の PS RoI pooling は fully convolutional という哲学でやっているので、それをぶち壊しにしないように、offset field 側も convolution で生成している。(普通の RoI pooling の deformable 版での offset filed は全結合層で生成していた)
Deformable ConvNets
- deformable conv は普通の conv と入出力が同じなので、入れ替えてそのまま使える
- ただし、offset field の重み初期値はゼロに (＝オフセットなしの普通の conv と同じ状態から始まるように) した
- モデルを最初から学習するのではなく、学習済みモデルに deformable の offset field を入れて追加で学習させる
- ただし細々した調整は入れてるよ (詳細は論文参照)
Deformable ConvNets の理解
- deformable convolution とは、「受容野は物体のスケールや形に合わせて適応すべき」という考え方に基づく (図5、図6，表2を見よ)
↑緑の点に注目したとき deformable conv によって拡散された受容野を赤い点でプロットしている。物体のスケールや形に合わせてちゃんと変わっていることがわかる。
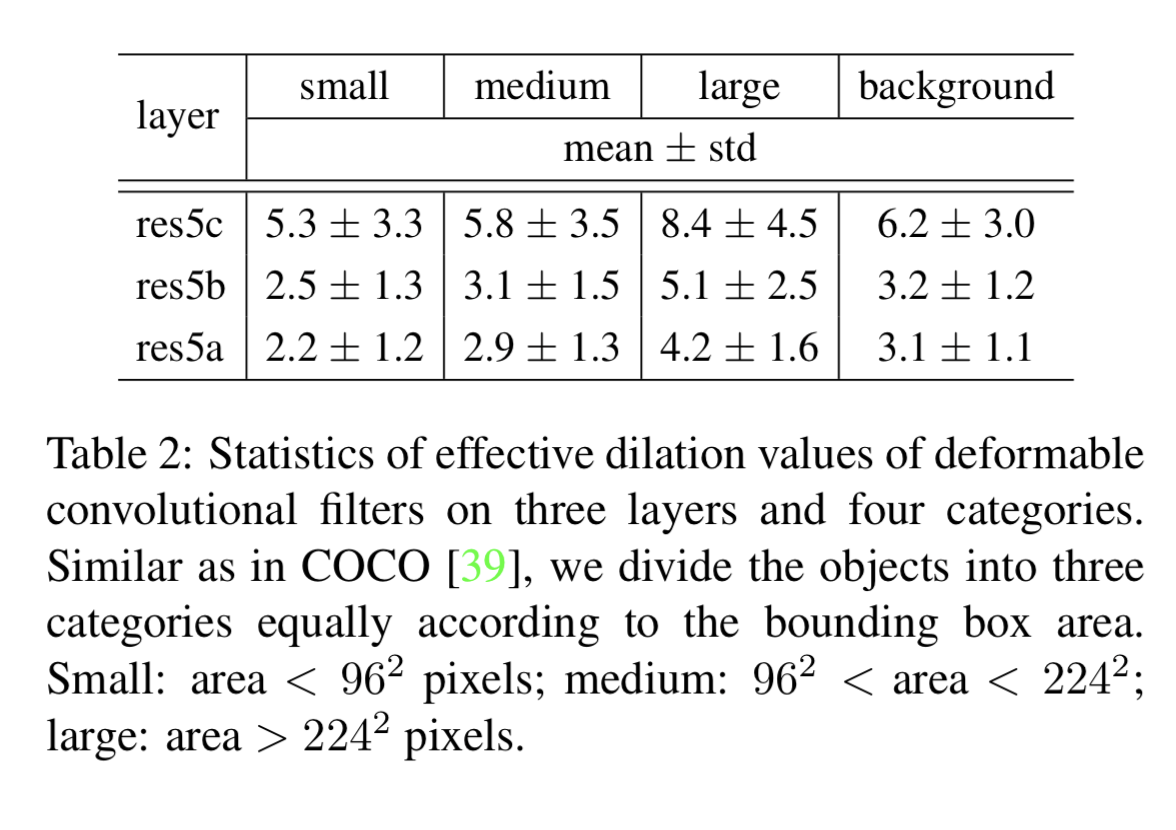
↓バウンディングボックスの大きさごとに、deformable conv で計算された受容野の広がりがどのくらいだったのかを計算した表。確かに、大きなバウンディングボックスの物体ほど受容野が広がっているのがわかる。
関連研究とのつながり
Spatial Transform Networks (STN)
- deformable conv の offset learning は、STN の spatial transformer の超軽量版とみなせる
- しかし、deformable conv ではあくまで局所的かつ密な方法で層を積み上げているという点に注意
Active Convolution
- active conv は提案法とほぼ同時に提案された手法 5
- deformable は「各ピクセルごとにオフセット」があり、active conv のほうは「各フィルタごとにオフセット」があるという違いはある
- また、deformable では入力が変わるとオフセットも応じて変わるが、active では固定 (もちろん学習対象ではある)
Effective Receptive Field
- 中心のほうが大事なはずなので受容野にガウス分布で重みを付けようという手法
- ERF は矩形の conv よりも層を重ねたときの受容野の広がりのオーダーが小さい (矩形：線形、ERF：平方根)
Atrous convolution 6
- すきっ歯なフィルタで畳み込みをかけるやつ
- deformable conv は atrous conv の一般化
ここから先にもまだまだ先行研究との比較が続くが割愛。気になる方は元論文を参照
実験
- semantic segmentation
- 実験結果で mIoU@V, mIoU@C と書かれているものが、それぞれ PASCAL VOC と Cityscapes の mean intersection over union score
- object detection
切除実験
どれを取り除くと影響が大きいかを調査
- Table1 から、deformable conv を使うと段々精度が上がっている様がわかる
- Table3 から、atrous conv の dialation rate を変えて実験してもやっぱり deformable のほうが強いことがわかる
- Table4 から、モデルのサイズ (パラメータ数) や処理速度にほぼ影響はないことがわかる
- 提案法の精度がよいのはパラメータ数が増えたからじゃなくて幾何的な変形を捕捉できるようになったからと言って良い
感想
- フィルタをずらすオフセットを学習するのではなく、ランダムに毎回ずらすというアプローチだけでも頑健性が上がりそうだと思った
- すでにありそうな気がする
- 長方形のフィルタで畳み込むのは完全にコンピュータ側の都合 (行列演算として書きたいという人間側の都合？) なので、そもそも長方形じゃなくて円形のフィルタとかで畳み込んだっていいよねと思った
- これもありそうな気がする。本文中で触れられている ERF (effective receptive field) がほぼそうか。graph-conv もコンセプトとしてやりたいことは近い？(情報の「近さ」って、ピクセルの座標の近さじゃないよね、ましてや矩形で切れるわけがないよねというコンセプト？フィルタの受容野はやりたいタスクで変えましょうねというコンセプト？)
- 長方形になっているのは、そもそも画像を表現するのに「ピクセル」という概念だからというものあると思う
- 画像の保存フォーマットとかではもはやピクセルではなく周波数情報しかもっていなさそうなので、そいつを直接処理したほうが本質的な情報だけになりそう
- これもありそう・・・7
- 画像の保存フォーマットとかではもはやピクセルではなく周波数情報しかもっていなさそうなので、そいつを直接処理したほうが本質的な情報だけになりそう
- G が bilinear なのは、式 (4) で定義できるような補完処理じゃないとうまく back-prop できないからっぽい？
- 式 (4) のように、bilinear だと各座標次元ごとの処理に分割できるので、確かにオフセットを畳み込みで表現しやすい。しかし、それが bilinear だけが持つ特徴なのかはあまりわからん・・・
-
原文：geometric ↩
-
論文中では、「q は入力特徴マップ全体の整数座標」となっているが、その直後の関数 G の説明 (式(4)) で、「近くの座標 (より正確には、縦横どちらの距離も1以下である座標) 以外での G の値はゼロ」としているため、わかりやすく言えば 「q は p の周辺の整数座標」と言っているのと同じこと ↩
-
offset field は、「各ピクセルごとに、そこを中心とした deformable conv のオフセット」をチャネル方向に持つ ↩
-
offset は N 個の矢印で決まる。各矢印の方向と大きさは、2次元なのでパラメータふたつ。よって 2N 個 ↩
-
深層学習コミュニティこわ近寄らんとこ ↩
-
dialated conv と言われることのほうが多い？ ↩
-
すごい方法を思いついてしまったかもしれない・・・→調べてみると大抵すでにある の法則 ↩