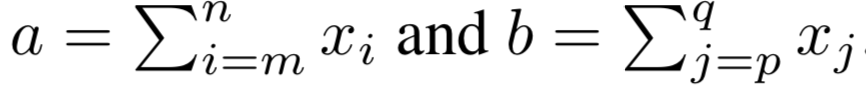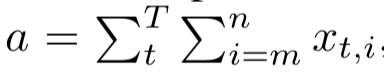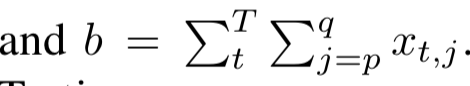[1808.00508] Neural Arithmetic Logic Units
メタ情報
- DeepMind, University of Oxford, University of College London
概要
- ニューラルネットは数値データの表現や処理に長けるが、訓練データの範囲外の数値に弱い
- 数値量を線形活性化で表現する、Neural Arithmetic Logic Units (NALU) を提案する
- 得られたモデルは外挿にも強くなった
導入
- 昆虫、哺乳類、そして人類は数値量を表現したり処理したりできる。このことは、これが知性の一般的な要素であることを示す
- 現在のニューラルネットが外挿に失敗するということは、学習が、システマチックな抽象化ではなく暗記によってなされていることを示唆する
- 非線形性のない個別のニューロンで数値量を表現し、単純な関数を表現可能な演算を適用する。全体としては微分可能性を保つ
- 様々な実験設定を試して結果を確認した：
- ドメイン：人工データ、画像、テキスト、コード
- 学習信号：教師付き、強化学習
- 構造：順伝播、リカレント
ニューラルネットの外挿失敗
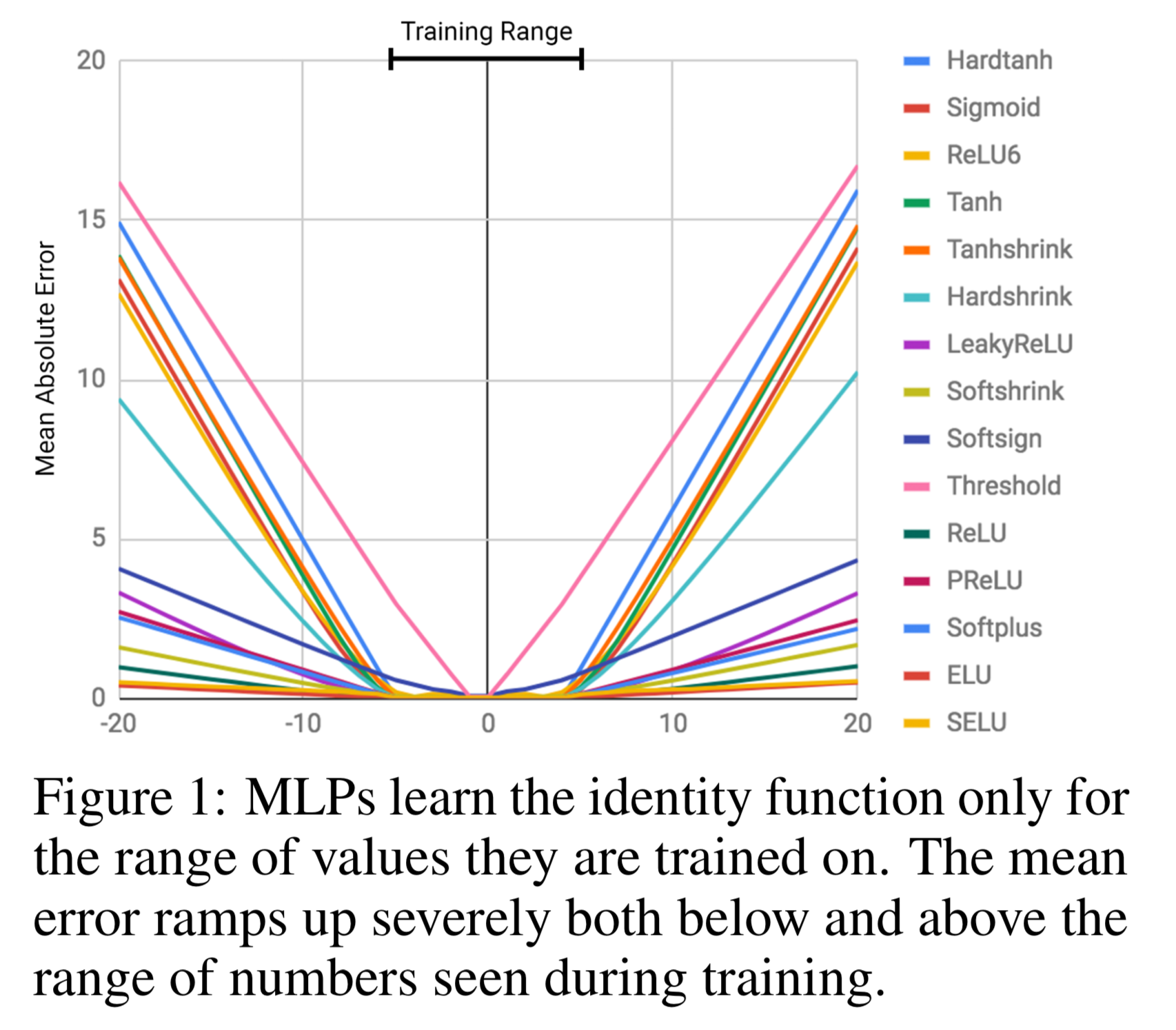
- MLP に恒等写像を学習させてみる
- いずれも理論上は学習可能だが、それでも失敗するということに注意
- 実験詳細は付録A
- スカラー値を入力してスカラー値を出力する auto-encoder
- ユニット数8の隠れ層3つ
- 10,000 iterations, 学習率 0.01, 二乗誤差
- 学習データは [-5, 5] でテストデータが [-20, 20]
ニューラル累算器 (NAC) とニューラル演算装置 (NALU) (The Neural Accumulator & Neural Arithmetic Logic Unit)
NAC
- 線形層の W の取りうる値を {-1, 0, +1} に制限する。すると、各入力ベクトルの要素の足し引きを表現できる。また、この演算では、入出力間のリスケールがおこなわれなくなる。(いくら重ねても)
- 実際には $W = \tanh (\hat{W}) \odot \sigma (\hat{M})$ として表現
- バイアス項や非線形活性化はなし
NALU
- 加減算ができれば乗算が可能になる
- ふたつの NAC セル (紫色の部分) と、ゲート (橙色の部分) からなる
- 加減算が必要ならゲートが1に、乗除算が必要ならゲートが0になる
- 小さい方の紫色は加減算をおこなう NAC セル。結果は $a$ と書くことにする
- 大きい方の紫色は乗除算をおこなう NAC セル。結果は $m$ と書くことにする
-
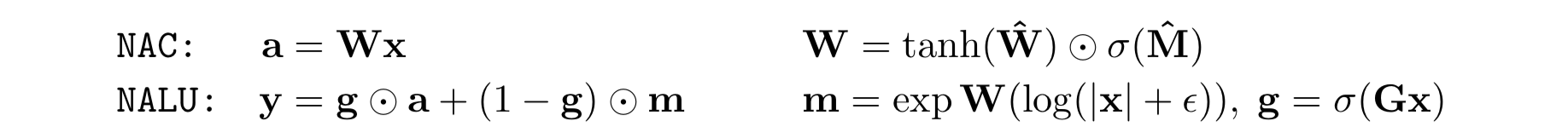
- W はパラメータを共有していることに注意
- NALU は加減乗除と冪算を学習可能
関連研究
- numerical reasoning (数値推論？) は、知性および深層学習の重要な研究トピックである
- 広く研究されているタスクは画像中のオブジェクト数え上げで、大きく2アプローチ：
-
- 各オブジェクトをセグメントし、あとで数え上げる
-
- end-to-end に個数を回帰しにいく
-
- 提案手法は 2) に近い
- 提案手法は深層学習の新しい活性化関数の提唱と見ることもできる
- 提案モデルは「magnitude は累算で操作される連続量として表現される」という仮定を唱える理論や、「各ニューロンが数字を表現する」という仮定を唱える理論を連想させる
- しかしながら多くの種では大きさが大きくなるほど連続量の近似が雑になる。提案モデルは固定精度。
実験
単純な関数の学習タスク
問題設定
- static task
- MLP 用
- $\boldsymbol{x} \in \mathbb{R}^{100}$ が与えられ、そのランダムな部分 (ランダムだが、問題ごとには固定) だけを2領域取り出して足し合わせたものを a, b とする
-
- a と b に対して単純な関数、たとえば加算や乗算を適用した結果 y を二乗誤差で予測するタスク
- 内挿問題は、訓練データの領域内での予測 (ただしホールドアウトはしている)
- 外挿問題は、訓練データの領域外での予測
- recurrent task
- LSTM 用
- $\boldsymbol{x}_t \in \mathbb{R}^{10}$ が与えられ、そのランダムな部分 (ランダムだが、問題ごとには固定) だけを2領域、しかも時系列に渡って取り出して足し合わせたものを a, b とする
-
- 外挿問題は、 $\boldsymbol{x}_t \in \mathbb{R}^{1000}$ のデータでおこなう (これをすると a, b, y の大きさは訓練データには十分出現しないような規模になる)
結果
- NAC は加減算は成功している。より柔軟な NALU は除算以外成功
MNIST 数え上げタスク
- 単純な関数の学習実験では入力がそのまま実数であったが、これを画像入力に変える
- MNIST 分類の CNN の上に recurrent network を載せて、10個のランダムな MNIST 画像を入力
- 数え上げタスクでは、各数字が何回出たかを 10-way 回帰
- 足し上げタスクでは、全数字の足し上げを線形回帰
- 外挿問題は、入力する MNIST データを 100 個や 1000 個に変更
- (長さ1で入力することで、分類問題としてそもそも解けているのかも計測している)
言語から数字への翻訳タスク
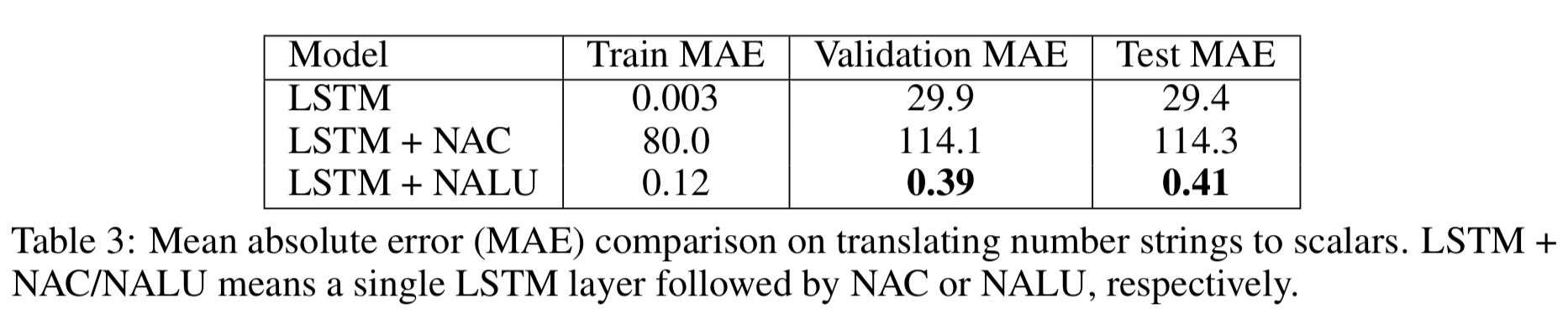
- "five hundred" とか "fifteen" とかをスカラ値に翻訳できるかの実験
- 0-1000 までのデータを扱う
- 訓練データは、 0-19 までと、残りの領域からランダムサンプルした合計 169 個
- ランダムサンプルしているのは、見たことのないトークンがあると困るから
- 残りを検証データ200個、評価データ631個とした
- Embedding -> LSTM -> Linear/NAC/NALU というアーキテクチャ
- NALU の結果が良いということは、このタスクは乗算が重要であるということを示唆している 1
プログラム実行 2
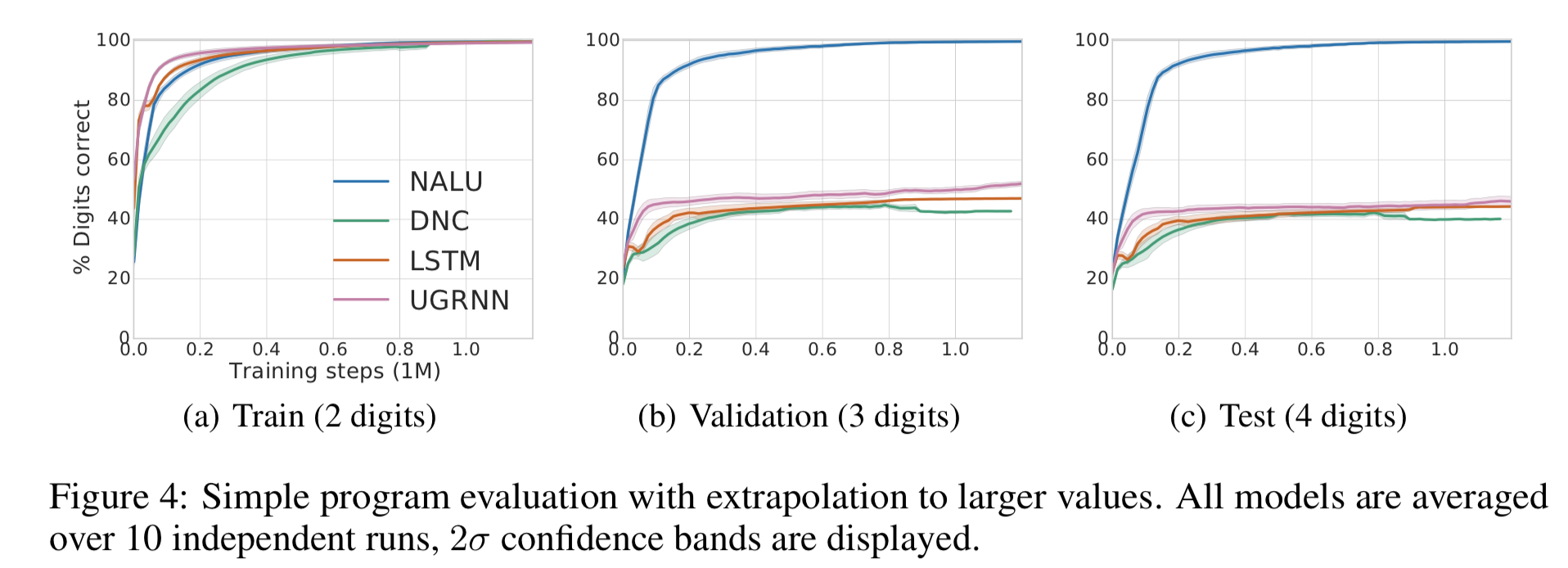
- プログラムスクリプトの評価は、論理・数値演算の制御と中間値の保持が要求される
- 2つの設定：
- 与えられた2つの整数の単純な足し算を表すプログラムの評価
- if文、+、- を含むようなプログラムの評価
- 与えるデータはすべて [0, 100) の整数値
- 訓練データ：2桁の整数
- 評価データ：3または4桁の整数
- 結果は NALU が一番良い
Track Time in a Grid-World Environment タスク
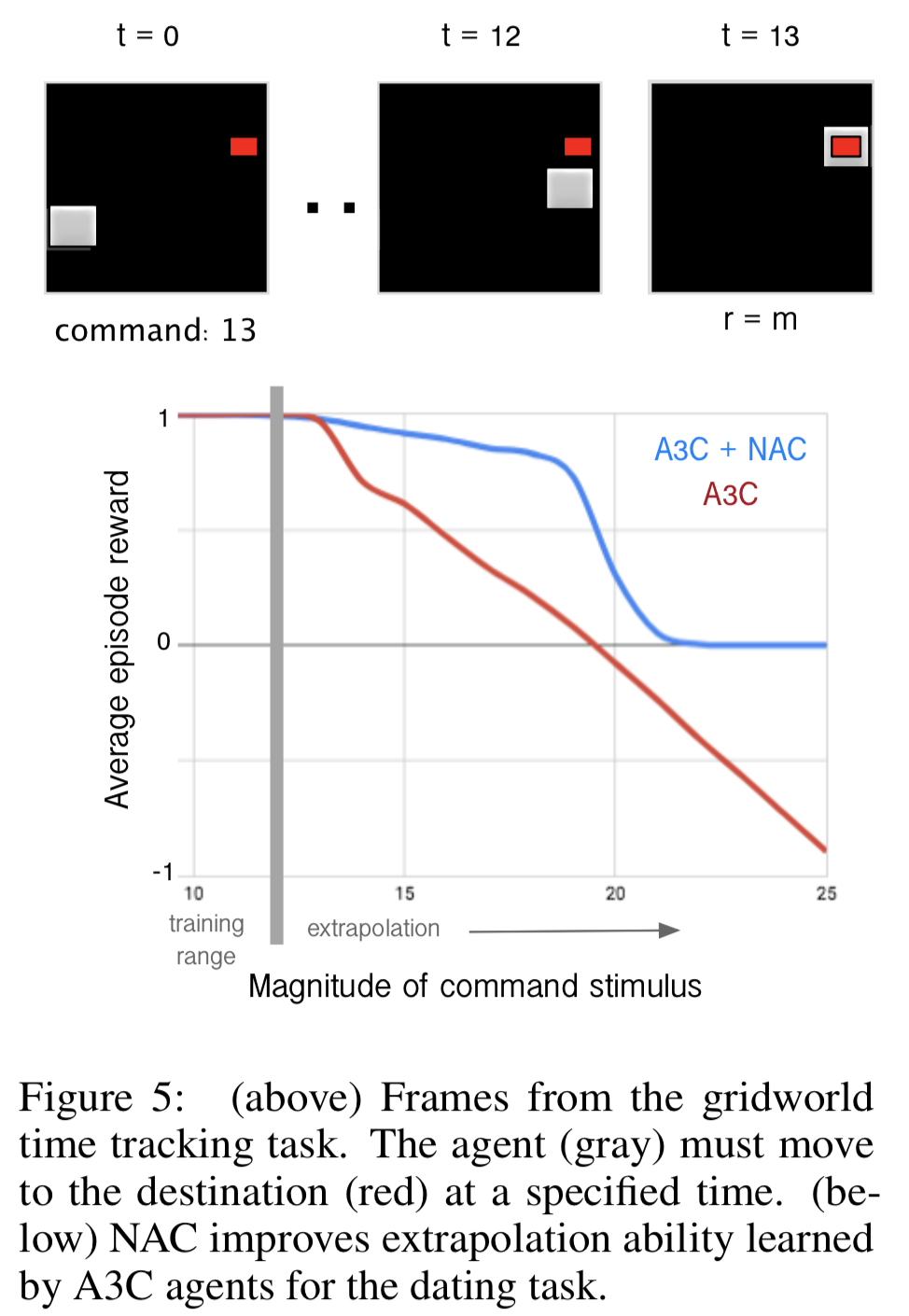
- 強化学習にも NAC が使えることを示す
- 5x5 の Grid-world 環境
- ただし状態は 56x56 pixel
- 行動は {UP, DOWN, LEFT, RIGHT, PASS}
- エージェントはエピソード開始時に数値 T を別個受け取り、ちょうど T ステップでゴールにたどり着いたときのみ報酬 m を貰える 3
- LSTM を使った A3C で実験
- T は、畳み込み層の結果にコンカチして LSTM のコアメモリに入力
- NAC を利用する場合は、LSTM への直接入力に加えて、T を NAC を通した結果も LSTM のコアメモリに入力
- 訓練データの T は 5-12 から生成
- 5x5 の grid なので、クリアが保証される最小の T は 8 である
- 学習されたエージェントの挙動
- A3C は 12 以上の T を「12」と解釈。早くゴールしすぎていた
- 一方 NAC は 20 以上の T で一切ゴールできていなかった
- これは、実験の設定上、LSTM への直接入力が残っているのでその影響のせいではないかと考えている
結論
(略)
参考資料
- [1808.00508] Neural Arithmetic Logic Units
- Neural Arithmetic Logic Units · Issue #879 · arXivTimes/arXivTimes
- [DL輪読会]Neural Arithmetic Logic Units (NALU)
- llSourcell/Neural_Arithmetic_Logic_Units: This is the code for "Neural Arithmetic Logic Units" By Siraj Raval on Youtube
感想
- 機械学習のよくある初心者向けの説明として「データ量が命で、データがなかったら学習もできない」ということが言われている。統計学的アプローチが大成功を収めているから確かにその通りなのだが、しかし、人工知能というからには、やっぱり真の意味での「抽象化」「論理推論」がなされていてほしいという気持ちもある
- few-shot learning 系の話とも関係ありそう？
- 結局このアーキテクチャでなんで if 文学習できるんだ？
- 論理推論が要求されるより実践的なタスクでの結果も見てみたい
- 実践的なタスクってなんだと聞かれると困るが・・・
- 強化学習タスクの実験例は興味深いのでもう少し考えてみたい