はじめに
本記事はPythonでAtcoderにチャレンジしているけど、Pythonはコード例がないため解説がわかりにくい!と感じている方を対象としています。
私自身大してレートも高くないので、不備等あるかもしれませんがご了承くださいm(_ _)m
質問や指摘などもコメント等に書いてくださったら対応していきたいと考えていますのでどしどしコメントしてください。(内容がわかりにくいぞ!みたいな文句でもオールオッケーです笑)
Toyota Programming Contest 2023 Spring Qual A C問題
問題のURLはこちらです。Toyota Programming Contest 2023 Spring Qual A C問題
使う手法
UnionFind木を使用しました。UnionFind木については前回の記事に簡単に書いていますので、よかったら見でください!!!!!(と言っても、他サイトの解説に丸投げしています笑)
ちなみに、今回実装したUnionFind木はそのサイトの実装例を丸コピしていますので、この先の考え方を見る際にはそのサイトを並行して見てみてください。
考え方
まず、「サイクルを持たない」ためには、グラフはどのような形になればよいでしょうか?
答えは簡単です。グラフが「森」(木の集まり)となれば、サイクルのないグラフと言えます。
なぜでしょうか?木構造のグラフの性質を見ていきたいと思います。
木構造グラフの性質その1
木構造のグラフには、閉路の非存在性について極大(木に新しく辺を加えると、絶対に閉路ができてしまう。)であるという性質があります。
もう少し踏み込んでいうと、N個の頂点があり、任意の2頂点を結ぶ道が一つ以上あるグラフについては、閉路を持たなければ木であると言えます。
わかりにくいのでN=4の以下に示すグラフで例を出します。
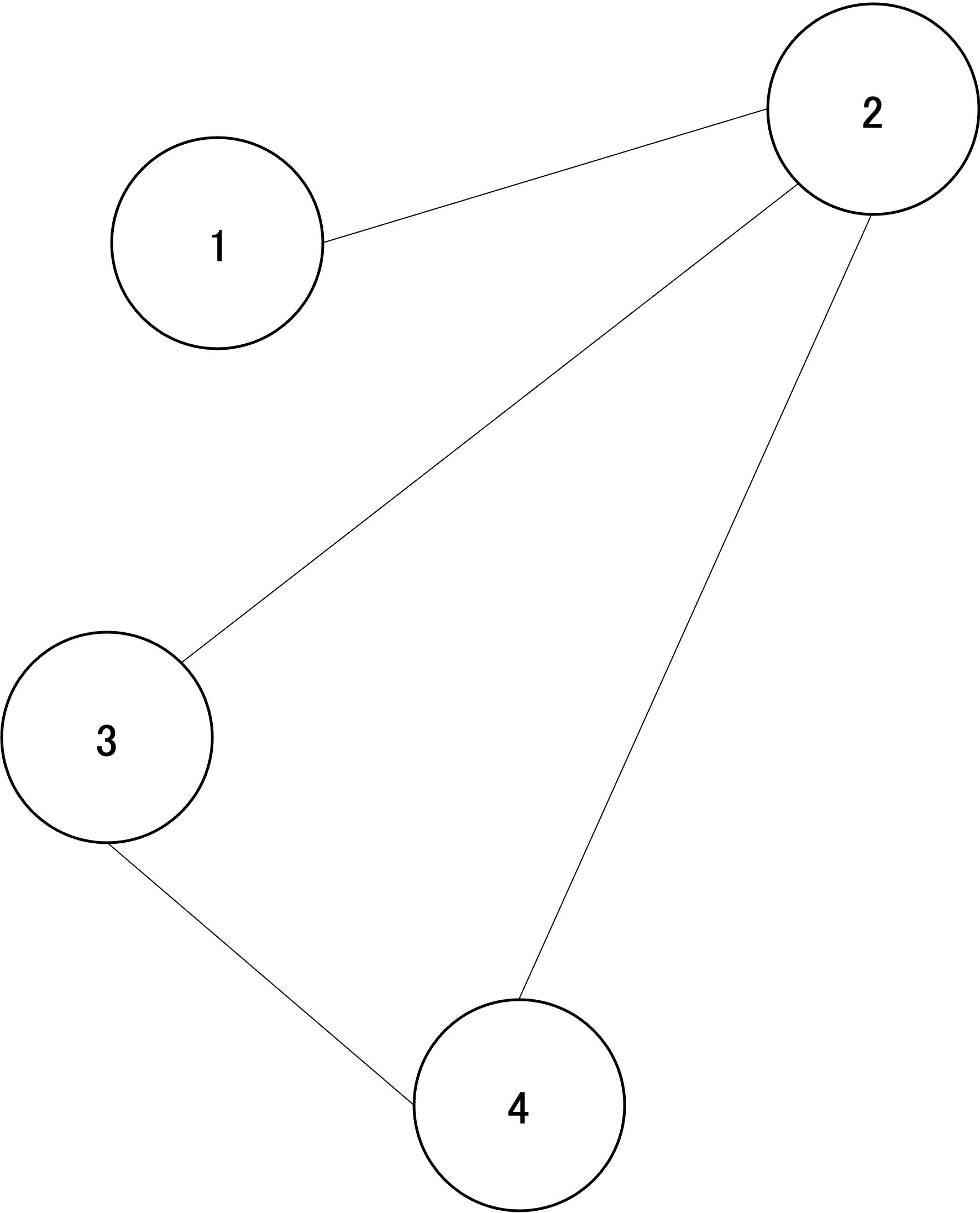
このグラフにおいて、頂点2-3-4で閉路ができていますが、ここからどの辺を抜き取っても木になります。
1-2の辺を抜き取ってもサイクルが残るじゃないか!と考える方もいるかと思いますが、これは先程の仮定である「任意の2頂点を結ぶ道が一つ以上あるグラフ」ではなくなってしまうため、1-2を抜き取ることは考えません。
今問題では各頂点が必ずつながっているという条件はないため、入力段階でつながっているもの同士をUnionFind木を用いて管理し、UnionFind木でグルーピングしたグラフが木構造かどうか、木構造でないなら何本辺を削除すればよいか考えていきます。
では、今問題のもう一つのポイントである木構造になるためには何本辺を削除すればよいかを考えていきます。
木構造グラフの性質その2
木構造のグラフには、もう一つ重要な性質があります。
それは、N個の頂点をもつ木構造グラフの辺の数はN-1本である というものです。
先程示したグラフを例に考えると、頂点数4に対し辺の数は4本ですから、木構造にするためには最低一本の辺を削除する必要があり、実際2-3-4から一本の辺を削除することで木構造にすることができます。
これを踏まえると、頂点数N、辺の数Mのグラフについて、M-(N-1)本の辺を削除することでサイクルをなくすことができます。(M-(N-1)が0以下の場合は、辺を削除せずともサイクルは持ちません)
今問題の解法
以上の性質を踏まえると、グラフがサイクルを持たないための最大限の辺の数$M_{max}$は、
M_{max} = \sum_{k=1}^{s} (N_k-1)
となります。($N_k$:分割されたk番目のグラフが持つ頂点の数,$s$:グラフの個数)
よって、与えられたMがM_maxを超過している場合は、超過している分だけ辺を削除すればよいですし、超過していないならサイクルを持たないので辺を削除する必要はありません。
具体例として、以下に示すN = 12、M = 11 のグラフを考えて問題を解いていきます。
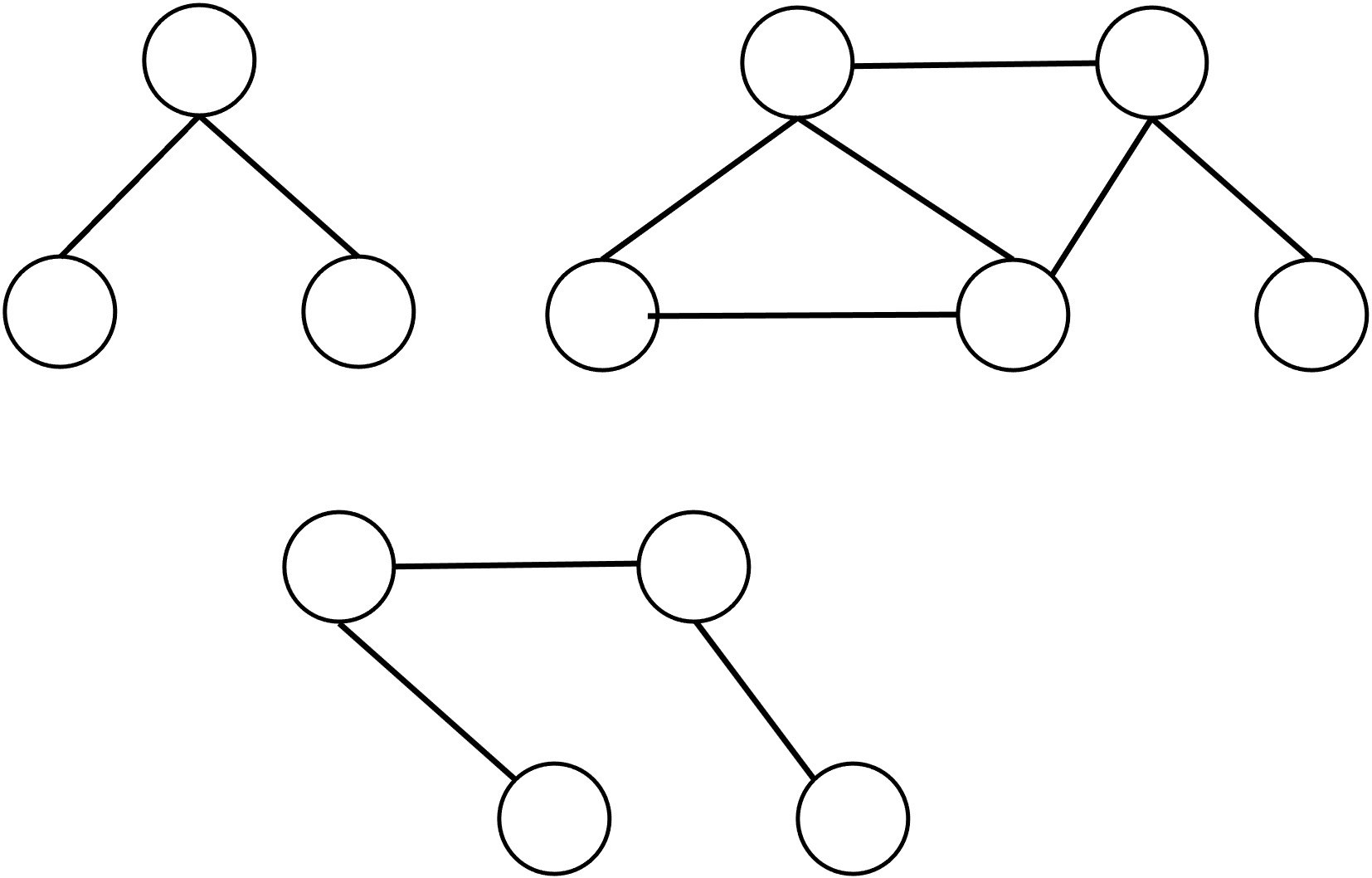
まず初めに、今問題ではグラフが三つあるので$s=3$となります。
次に最小の辺の数について、左上のグラフは頂点数が3つあるので必要な辺の数は2本、
右上のグラフについては、頂点数が5なので必要な辺の数は4本、
下のグラフについては、頂点数が3つなので必要な辺の数は3本です。
よって、今回のグラフがサイクルを持たないために必要な最大限の辺の数は2+3+4=9本であり、今問題では11本の辺が存在するため、2本の辺を取り除くことでサイクルがなくなります。
よって、出力する値は2となります。
実装例
from collections import defaultdict
#UnionFindクラスの設定
class UnionFind():
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x):
return -self.parents[self.find(x)]
def same(self, x, y):
return self.find(x) == self.find(y)
def members(self, x):
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
return len(self.roots())
def all_group_members(self):
group_members = defaultdict(list)
for member in range(self.n):
group_members[self.find(member)].append(member)
return group_members
def __str__(self):
return '\n'.join(f'{r}: {m}' for r, m in self.all_group_members().items())
n,m = map(int,input().split())
#UnionFindの構築
uf = UnionFind(n)
#辺のつながりを受け取り、UnionFindでグルーピング
for _ in range(m):
a,b = map(int,input().split())
uf.union(a-1,b-1)
#max_edge->全てが木構造となる最大の辺数を格納する。
max_edge = 0
for i in range(len(uf.parents)):
node_parent = uf.parents[i]
#各グループの頂点の数「uf.size(i)」を取得し、それをもとに木構造に必要な辺の数をmax_edgeに加える
if node_parent < 0 :
max_edge += uf.size(i)-1
if m-max_edge >= 0 :
print(m-max_edge)
else :
print(0)
留意点
グラフがサイクルを持たないための最大限の辺の数$M_{max}$という風に書いていますが、これはあくまで現状のグルーピングを壊さないという前提があることに留意してください。
図で示した、N = 12、M = 11 のグラフは、グループ同士をつなげることを許容すれば、9本から辺の数を増やしてもサイクルはできません。
ですが、今問題はあくまで「与えられたグラフから何本消せばよいか」が問題です。したがって、各グルーピングの要素を増やさず木構造にするにはどうすべきかというアプローチが必要でした。
最後に
自分で書いてても、今回の解説記事は特にわかりにくいだろうなーと感じます。
なので、わかりにくいところなどは遠慮なくコメントで聞いてくださるとありがたいです。