Part 2 統計的推定
Chap.0 全体の流れ
Part2では、統計的推定を行う。自然科学では、調査対象(自然)は直接全て調査することができないので、標本調査が一般的である。
その際、得られた標本(母集団の一部)から、未知の母集団全体の分布を推定するのが、統計的推定である。
Chap.1 ライブラリの読み込み
%matplotlib inline
import numpy as np
from scipy import stats
import math
import pandas as pd
from matplotlib import pyplot as plt
最初に、必要なライブラリの読み込みから始める。1行目は、Part 1同様にmatplotlibをJupyter Notebook内で表示するためのマジックコマンドである。
2行目以降が、今回利用するライブラリである。これらのライブラリのうち、mathライブラリはPythonに標準で組み込まれている。また、それ以外のライブラリはAnacondaにインストールされている。
ちなみに、mathとNumpyは機能が類似しているが、mathは標準のPythonに組み込まれている関数で、Numpyは複雑な数値計算を効率的にする拡張モジュールであり、その役割は異なる。
| ライブラリ | 概要 | 今回の使用目的 | 公式URL |
|---|---|---|---|
| NumPy | 数値計算ライブラリ | 統計処理上の数値計算に利用 | https://www.numpy.org |
| Scipy | 科学計算ライブラリ | 統計的推定の計算に利用 | https://www.scipy.org |
| math | 標準の数値計算ライブラリ | 平方根などのかんたんな計算に利用 | https://docs.python.org/ja/3/library/math.html |
| pandas | データ分析ライブラリ | データ読み込みや整形に利用 | https://pandas.pydata.org |
| Matplotlib | グラフ描画ライブラリ | データの可視化に利用 | https://matplotlib.org |
Chap.2 データの読み込み
今回はカツオ(Katsuwonus pelamis)のデータを利用する。Part 0のChap.4を参照し、ChemTHEATREのSample Searchから、カツオのサンプルデータを計測データをダウンロードする。
ダウンロードできたら、このノートブックファイルのあるフォルダにmeasureddataとsamplesのデータを移動する。その後Anacondaを起動し直した後に、Part 1同様にpandasのread_csv関数を利用して、計測データと試料データの双方を読み込む。
data_file = "measureddata_20190930045953.tsv" #変数に入力する文字列を、各自のmeasureddataのtsvファイル名に変更する
chem = pd.read_csv(data_file, delimiter="\t")
chem = chem.drop(["ProjectID", "ScientificName", "RegisterDate", "UpdateDate"], axis=1) #後でsamplesと結合する際に重複する列の削除
sample_file = "samples_20190930045950.tsv" #変数に入力する文字列を、各自のsamplesのtsvファイル名に変更する
sample = pd.read_csv(sample_file, delimiter="\t")
pythonのようにプログラムでファイルを読み込んだり、加工したりした際は、想定したとおりにファイルが読み込めているか確認する癖付けをしておいたほうが良い。ちなみにJupyter Notebookの場合、変数名のみ入力すると、その変数の中身がOutに表示されるので便利である。
chem
| MeasuredID | SampleID | ChemicalID | ChemicalName | ExperimentID | MeasuredValue | AlternativeData | Unit | Remarks | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | SAA000001 | CH0000096 | ΣPCBs | EXA000001 | 6.659795 | NaN | ng/g wet | NaN |
| 1 | 2 | SAA000002 | CH0000096 | ΣPCBs | EXA000001 | 9.778107 | NaN | ng/g wet | NaN |
| 2 | 3 | SAA000003 | CH0000096 | ΣPCBs | EXA000001 | 5.494933 | NaN | ng/g wet | NaN |
| 3 | 4 | SAA000004 | CH0000096 | ΣPCBs | EXA000001 | 7.354636 | NaN | ng/g wet | NaN |
| 4 | 5 | SAA000005 | CH0000096 | ΣPCBs | EXA000001 | 9.390950 | NaN | ng/g wet | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 74 | 75 | SAA000082 | CH0000096 | ΣPCBs | EXA000001 | 3.321208 | NaN | ng/g wet | NaN |
| 75 | 76 | SAA000083 | CH0000096 | ΣPCBs | EXA000001 | 3.285111 | NaN | ng/g wet | NaN |
| 76 | 77 | SAA000084 | CH0000096 | ΣPCBs | EXA000001 | 0.454249 | NaN | ng/g wet | NaN |
| 77 | 78 | SAA000085 | CH0000096 | ΣPCBs | EXA000001 | 0.100000 | <1.00E-1 | ng/g wet | NaN |
| 78 | 79 | SAA000086 | CH0000096 | ΣPCBs | EXA000001 | 0.702224 | NaN | ng/g wet | NaN |
79 rows × 9 columns
sample
| ProjectID | SampleID | SampleType | TaxonomyID | UniqCodeType | UniqCode | SampleName | ScientificName | CommonName | CollectionYear | ... | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | PRA000001 | SAA000001 | ST008 | 8226 | es-BANK | EF00564 | NaN | Katsuwonus pelamis | Skipjack tuna | 1998 | ... |
| 1 | PRA000001 | SAA000002 | ST008 | 8226 | es-BANK | EF00565 | NaN | Katsuwonus pelamis | Skipjack tuna | 1998 | ... |
| 2 | PRA000001 | SAA000003 | ST008 | 8226 | es-BANK | EF00566 | NaN | Katsuwonus pelamis | Skipjack tuna | 1998 | ... |
| 3 | PRA000001 | SAA000004 | ST008 | 8226 | es-BANK | EF00567 | NaN | Katsuwonus pelamis | Skipjack tuna | 1998 | ... |
| 4 | PRA000001 | SAA000005 | ST008 | 8226 | es-BANK | EF00568 | NaN | Katsuwonus pelamis | Skipjack tuna | 1998 | ... |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 74 | PRA000001 | SAA000082 | ST008 | 8226 | es-BANK | EF00616 | NaN | Katsuwonus pelamis | Skipjack tuna | 1999 | ... |
| 75 | PRA000001 | SAA000083 | ST008 | 8226 | es-BANK | EF00617 | NaN | Katsuwonus pelamis | Skipjack tuna | 1999 | ... |
| 76 | PRA000001 | SAA000084 | ST008 | 8226 | es-BANK | EF00619 | NaN | Katsuwonus pelamis | Skipjack tuna | 1999 | ... |
| 77 | PRA000001 | SAA000085 | ST008 | 8226 | es-BANK | EF00620 | NaN | Katsuwonus pelamis | Skipjack tuna | 1999 | ... |
| 78 | PRA000001 | SAA000086 | ST008 | 8226 | es-BANK | EF00621 | NaN | Katsuwonus pelamis | Skipjack tuna | 1999 | ... |
79 rows × 66 columns
Chap.3 データの下処理
データの読み込みが完了したら、次はデータの下処理を行う。
まず、2つに分かれているデータ(chemとsample)を統合し、必要なデータのみ抽出する。今回は、カツオのΣPCBのデータを利用したいので、"ChemicalName"列の値が"ΣPCB"のデータのみを抽出する。
df = pd.merge(chem, sample, on="SampleID")
data = df[df["ChemicalName"] == "ΣPCBs"]
続いて、計測データの単位が異なっているかどうかを確認する。Part 1のようにデータの単位が異なっていると単純に比較や統合ができないからである。
data["Unit"].unique()
array(['ng/g wet'], dtype=object)
pandasのuniqueメソッドを利用すると、そのデータフレーム内に含まれる値の一覧を見ることができる。ここで、"Unit"列に含まれる値の一覧を出力してみると、"ng/g wet"のみである事がわかるので、今回は、単位によるデータの分割は不要である。
最後は、N/Aしかない列を削除して、データの下処理は完了である。
data = data.dropna(how='all', axis=1)
data
| MeasuredID | SampleID | ChemicalID | ChemicalName | ExperimentID | MeasuredValue | AlternativeData | Unit | ProjectID | SampleType | ... | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | SAA000001 | CH0000096 | ΣPCBs | EXA000001 | 6.659795 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 1 | 2 | SAA000002 | CH0000096 | ΣPCBs | EXA000001 | 9.778107 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 2 | 3 | SAA000003 | CH0000096 | ΣPCBs | EXA000001 | 5.494933 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 3 | 4 | SAA000004 | CH0000096 | ΣPCBs | EXA000001 | 7.354636 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 4 | 5 | SAA000005 | CH0000096 | ΣPCBs | EXA000001 | 9.390950 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 74 | 75 | SAA000082 | CH0000096 | ΣPCBs | EXA000001 | 3.321208 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 75 | 76 | SAA000083 | CH0000096 | ΣPCBs | EXA000001 | 3.285111 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 76 | 77 | SAA000084 | CH0000096 | ΣPCBs | EXA000001 | 0.454249 | NaN | ng/g wet | PRA000001 | ST008 | ... |
| 77 | 78 | SAA000085 | CH0000096 | ΣPCBs | EXA000001 | 0.100000 | <1.00E-1 | ng/g wet | PRA000001 | ST008 | ... |
| 78 | 79 | SAA000086 | CH0000096 | ΣPCBs | EXA000001 | 0.702224 | NaN | ng/g wet | PRA000001 | ST008 | ... |
79 rows × 35 columns
Chap.4 点推定
標本から母集団を推測する、統計的推定のうち、ピンポイントで値を推定するのが点推定である。ここでは、カツオから検出されたΣPCB濃度の標本から、母集団(採集地域での個体全体)のΣPCB濃度を推定してみる。
まず、年ごとに計算しその変化の推移を見るために、何年のデータが含まれているかを確認する。
data['CollectionYear'].unique()
array([1998, 1997, 1999, 2001], dtype=int64)
上のuniqueメソッドから1997~1999年の3年間と2001年のデータがデータセットに含まれていることがわかった。ここでまずは、1997年のデータを取り出してみる。この際、今後の計算が楽になるように取り出したデータをNumpyのndarray1形式に変更しておく。
pcb_1997 = np.array(data[data['CollectionYear']==1997]["MeasuredValue"]) # 1997年の測定値のみを抽出
pcb_1997
array([ 10.72603788, 9.22208078, 7.59790835, 30.95079465,
15.27462553, 14.15719633, 13.28955903, 14.87712806,
9.86650189, 18.26554514, 3.39951845, 6.58172781,
12.43564814, 6.1948639 , 6.41605666, 4.98827291,
12.36669815, 31.17955551, 8.16184346, 4.60893266,
36.85826409, 52.99841724, 39.22500351, 53.92302702,
69.4308048 , 73.97686479, 125.3887794 , 45.39974771,
54.12726127, 39.77794045, 101.2736126 , 38.06220403,
126.8301693 , 70.25308435, 31.24246301, 21.3958656 ,
41.85726522, 30.91112132, 81.12597135, 10.76755148,
24.20442213, 24.57497594, 14.84353549, 59.53687389,
52.78443082, 8.4644697 , 4.15293758, 3.31957452,
4.51832675, 6.98373973])
同様に1998年と1999年のデータも抽出する。
pcb_1998 = np.array(data[data['CollectionYear']==1998]["MeasuredValue"]) # 1998年の測定値のみを抽出
pcb_1999 = np.array(data[data['CollectionYear']==1999]["MeasuredValue"]) # 1999年の測定値のみを抽出
ここで、平均と分散の不偏推定量を算出する。
まず、平均の不偏推定量($\hat{\mu}$)だが、これは標本平均($\overline{X}$)の期待値が母平均と等しいことを利用する。(下式参照)
$$ E \left(\overline X \right) = E\left(\frac{1}{n} \sum_{i=1}^{n} \left(x_i\right)\right) = \frac{1}{n}\sum_{i=1}^{n} E\left(x_i\right) = \frac{1}{n} \times n\mu = \mu \\ \therefore \hat\mu = \overline{x} $$
s_mean_1997 = np.mean(pcb_1997)
s_mean_1997
31.775384007760003
同様に、分散の不偏推定量を算出する。
このとき標本分散($S^2$)の期待値は、母分散($\sigma^2$)と同じ値は取らず、代わりに不偏分散($s^2$)を求める必要があることに注意する。
$$\hat\sigma^2 \neq S^2 = \frac{1}{n} \sum_{i=1}^{n} \left( x_i - \overline X \right) \\ \hat\sigma^2 = s^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left( x_i - \overline X \right)$$
なお、Numpyのvar関数は、どちらの分散も算出することができ、不偏分散はddof=1のパラメータで出力される。ただし、デフォルトではddof=0の標本分散が出力させるので注意が必要である。
$$\mathrm{np.var}\left(x_1 \ldots x_n, \mathrm{ddof=0}\right): S^2 = \frac{1}{n} \sum_{i=1}^{n} \left( x_i - \overline X \right) \\
\mathrm{np.var}\left(x_1 \ldots x_n, \mathrm{ddof=1}\right): \hat\sigma^2 = \frac{1}{n-1} \sum_{i=1}^{n} \left( x_i - \overline X \right)$$
u_var_1997 = np.var(pcb_1997, ddof=1)
u_var_1997
942.8421749786518
同様に、1998年と1999年の平均と分散の不偏推定量を算出する。
s_mean_1998, s_mean_1999 = np.mean(pcb_1998), np.mean(pcb_1999)
u_var_1998, u_var_1999 = np.var(pcb_1998, ddof=1), np.var(pcb_1999, ddof=1)
ここで、求めた代表値について整理する。まず、
s_mean_1997, s_mean_1998, s_mean_1999
(31.775384007760003, 17.493267312533337, 30.583242522000003)
u_var_1997, u_var_1998, u_var_1999
(942.8421749786518, 240.2211176248311, 1386.7753819003349)
Chap.5 区間推定と信頼区間
Chap.5では、Chap.4で求めた点推定とは異なり、母平均や母分散を統計的に一定の範囲で推定する区間推定をする。
Sec.5-1 母平均の区間推定
まず、区間推定をする前に、各年のデータセットのデータ数を調べる。データ数は、pythonに標準で実装されているlen関数を利用すれば、算出できる。
n_1997 = len(pcb_1997)
n_1997
50
n_1998, n_1999 = len(pcb_1998), len(pcb_1999)
n_1998, n_1999
(15, 13)
上記から、1997年~1999年の各年のデータセットのデータ総数がわかった。
この内、1997年のデータセットは、$n = 50$と大標本であり、1998年・1999年のデータセットは、それぞれ$n = \left\{ \begin{array}{ll}15 & \left( 1998 \right) \\ 13 & \left( 1999 \right) \end{array} \right.$で、小標本である。
したがって、このあとの区間推定の処理が少々異なることに注意する必要がある。
まず1997年のデータセットから、母平均の区間推定をする。この場合、母分散未知で大標本($n > 30$)なので、中心極限定理から標本平均($\overline X $)は正規分布 $N\left( \mu , \frac{s^2}{n} \right)$を近似することができる。なので、母平均を信頼度($\alpha$)で区間推定すると、信頼区間は下式のようになる。
$\overline X - z_\frac{\alpha}{2} \sqrt{\frac{s^2}{n}} < \mu < \overline X - z_\frac{\alpha}{2} \sqrt{\frac{s^2}{n}} $pythonではScipyのstas.norm.interval()を利用すると、平均(loc)・標準偏差(scale)の正規分布でalpha×100%となる範囲を、中央値を中心として取得できる。
ここで、信頼度($\alpha = 0.95$)で信頼区間を算出する。
m_interval_1997 = stats.norm.interval(alpha=0.95, loc=s_mean_1997, scale=math.sqrt(pcb_1997.var(ddof=1)/n_1997))
m_interval_1997
(23.26434483549182, 40.28642318002819)
次に、1998年、1999年のデータセットについて母平均の区間推定をする。これらは、母分散が未知で、小標本($n\leq 30$)である。この場合、母平均$\mu$は、正規分布$ N \left( \mu , \frac{s^2}{n} \right)$ではなく、自由度($n-1$)のt分布を利用する。なので、母平均を信頼度($\alpha$)で区間推定すると、信頼区間は下式のようになる。
$\overline X - t_\frac{\alpha}{2}\left(n-1\right)\sqrt{\frac{s^2}{n}} < \mu < \overline X + t_\frac{\alpha}{2}\left(n-1\right)\sqrt{\frac{s^2}{n}} $pythonでは、stats.t.interval()を利用すると、平均(loc)・標準偏差(scale)・自由度(df)のt分布でalpha×100%となる範囲を、中央値を中心として取得できる。
ここでは、信頼度($\alpha = 0.95 $)で信頼区間を算出する。
m_interval_1998 = stats.t.interval(alpha=0.95, df=n_1998-1, loc=s_mean_1998, scale=math.sqrt(pcb_1998.var(ddof=1)/n_1998))
m_interval_1999 = stats.t.interval(alpha=0.95, df=n_1999-1, loc=s_mean_1999, scale=math.sqrt(pcb_1999.var(ddof=1)/n_1999))
m_interval_1997, m_interval_1998, m_interval_1999
((23.26434483549182, 40.28642318002819),
(8.910169386248537, 26.076365238818138),
(8.079678286109523, 53.086806757890486))
なお、95%信頼区間とは、母平均が95%の確率でその範囲にあるということを表している。つまり、信頼度($\alpha$)を小さくすると、母平均が信頼区間に含まれる確率が小さくなると同時に、信頼区間は狭くなる。
stats.norm.interval(alpha=0.9, loc=s_mean_1997, scale=math.sqrt(pcb_1997.var(ddof=1)/n_1997))
(24.63269477364296, 38.91807324187704)
Sec.5-2 母分散の区間推定
次に、母分散の区間推定をする。母分散($\sigma^2$)の区間推定では、$\frac{\left(n-1\right)s^2}{\sigma^2}$が、自由度$(n-1)$の$\chi^2$分布に従うことを利用する。
$\chi_\frac{\alpha}{2}\left(n-1\right) \leq \frac{\left( n-1 \right)s^2}{\sigma^2} \leq \chi_{1-\frac{\alpha}{2}}\left(n-1\right)$まず、自由度($n-1$)の$\chi^2$分布のパーセント点($\chi_\frac{\alpha}{2}\left(n-1\right), \chi_{1-\frac{\alpha}{2}}\left(n-1\right)$)を求める。ここでは、信頼度0.95で計算する。
なお、pythonではScipyのstats.chi2.interval()で、自由度(df)のalpha×100%となる範囲が取得できる。
chi_025_1997, chi_975_1997 = stats.chi2.interval(alpha=0.95, df=n_1997-1)
chi_025_1997, chi_975_1997
(31.554916462667137, 70.22241356643451)
続いて、信頼区間を求める。導出には、以下の式を参考にする。
$\frac{\left(n-1\right)s^2}{\chi_\frac{\alpha}{2}\left(n-1\right)} \leq \sigma^2 \leq \frac{\left(n-1\right)s^2}{\chi_{1-\frac{\alpha}{2}}\left(n-1\right)}$v_interval_1997 = (n_1997 - 1)*np.var(pcb_1997, ddof=1) / chi_975_1997, (n_1997 - 1)*np.var(pcb_1997, ddof=1) / chi_025_1997
v_interval_1997
(657.8991553778869, 1464.0909168183869)
同様に、1998年、1999年のデータセットに関しても、分散の区間推定をする。なお、母平均の区間推定とは異なり、$\frac{\left(n-1\right)s^2}{\sigma^2}$の分布は、標本サイズに関わらず、$\chi^2$分布に従う。
chi_025_1998, chi_975_1998 = stats.chi2.interval(alpha=0.95, df=n_1998-1)
chi_025_1999, chi_975_1999 = stats.chi2.interval(alpha=0.95, df=n_1999-1)
v_interval_1998 = (n_1998 - 1)*np.var(pcb_1998, ddof=1) / chi_975_1998, (n_1998 - 1)*np.var(pcb_1998, ddof=1) / chi_025_1998
v_interval_1999 = (n_1999 - 1)*np.var(pcb_1999, ddof=1) / chi_975_1999, (n_1999 - 1)*np.var(pcb_1999, ddof=1) / chi_025_1999
v_interval_1997, v_interval_1998, v_interval_1999
((657.8991553778869, 1464.0909168183869),
(128.76076176378118, 597.4878836139195),
(713.0969734866349, 3778.8609867211235))
chi_025_1997, chi_975_1997 = stats.chi2.interval(alpha=0.9, df=n_1997-1)
(n_1997 - 1)*np.var(pcb_1997, ddof=1) / chi_975_1997, (n_1997 - 1)*np.var(pcb_1997, ddof=1) / chi_025_1997
(696.4155490924242, 1361.5929987004467)
Chap.6 推定結果の可視化
それでは、Chap.4・Chap.5で推定した母平均をグラフに可視化する。
まず、Chap.4で点推定した母平均の値を時系列にまとめる。
x_list = [1997, 1998, 1999]
y_list = [s_mean_1997, s_mean_1998, s_mean_1999]
次に、Chap.5で推定した、信頼度95%の母平均の信頼区間も時系列にまとめる。
interval_list = []
interval_list.append(m_interval_1997)
interval_list.append(m_interval_1998)
interval_list.append(m_interval_1999)
interval_list
[(23.26434483549182, 40.28642318002819),
(8.910169386248537, 26.076365238818138),
(8.079678286109523, 53.086806757890486)]
母平均の95%信頼区間は、このままでは可視化に利用できないので、信頼区間の幅を求める。
interval_list = np.array(interval_list).T[1] - y_list
x_list, y_list, interval_list
([1997, 1998, 1999],
[31.775384007760003, 17.493267312533337, 30.583242522000003],
array([ 8.51103917, 8.58309793, 22.50356424]))
最後に、matplotlibで可視化する。信頼区間は、エラーバーで表示する。matplotlibでエラーバーを表示する際は、errorbarメソッドを利用する。
このメソッドでは、X軸の値(ここでは年)、Y軸の値(ここでは点推定の母平均)、エラーバーの長さ(ここでは信頼区間の幅)を指定する。
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.errorbar(x=x_list, y=y_list, yerr=interval_list, fmt='o-', capsize=4, ecolor='red')
plt.xticks(x_list)
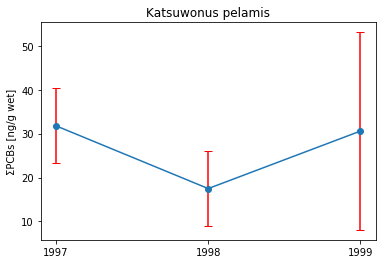
ax.set_title("Katsuwonus pelamis")
ax.set_ylabel("ΣPCBs [ng/g wet]")
plt.show()
脚注
1Numpyでのn次行列を格納するデータ形式。