はじめに
ADALINE を一から実装したのでそのまとめ
ADALINE とパーセプトロンの違い
-
重みの更新方法
- パーセプトロンは単位ステップ関数で重みの更新を行います
- ADALINE は挿入力の高等関数を使う(Hidrow-Hoff 測と呼ばれます)
φ(w^Tx) = w^Tx
-
クラスラベルの予測
- パーセプトロンは活性化関数をそのまま出力します
- ADALINE は量子化器を使います
コスト関数の定義
教師あり学習を構成する要素として、最適化される目的関数を定義することがあります。
多くの場合にはこの目的関数は最小化したいコスト関数です。ADALINE ではコスト関数$J(w)$として定義します。
ADALINE の場合計算結果と本当のクラスラベルとの誤差平方和をとります。
J(w) = \frac{1}{2}\sum_i(y^{(i)}-φ(z^{(i)}))^2
重みベクトル$w$の各重み$w_i$は同時に更新され以下の式で表されます。
w_i := w_i + \Delta w_i
$\Delta w_i$の計算は以下のようにされます。
\Delta w_i = \eta(y_i - \breve{y_i})x_i^{(i)}
$\eta$は学習率で$0<\eta<1$です。
$y_i$はトレーニングクラスラベルで$\breve{y_i}$は予測クラスラベルです。
ADALINE の実装
実装環境
-
python 3.6
-
JupyterLab 0.35.4
コード
コスト関数の最小化については勾配降下法を使っています。
class AdalineGD(object):
"""
パラメータ
eta:学習率
n_iter:トレーニング回数
属性
w_:一次元配列、適合後の重み
errors_:リスト、各エポックでの誤分類数
"""
def __init__(self,eta = 0.01,n_iter = 50):
self.eta = eta
self.n_iter = n_iter
def fit(self,X,y):
"""
パラメータ
X:配列のようなデータ構造,shape = {n_sample,n_features}
n_samplesはサンプルの個数、n_featuresは特徴量の個数
y:目的変数
戻り値
self:object
"""
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
#トレーニング回数分トレーニングデータを反復
for i in range(self.n_iter):
#活性化関数の出力の計算
output = self.net_input(X)
#誤差の計算
errors = (y-output)
#w1以降の更新
self.w_[1:] += self.eta*X.T.dot(errors)
#w0の更新
self.w_[0] += self.eta*errors.sum()
#コスト関数の計算(勾配降下法)
cost = (errors**2).sum()/2.0
#コストの格納
self.cost_.append(cost)
return self
#挿入力の計算
def net_input(self,X):
return np.dot(X,self.w_[1:])+self.w_[0]
#活性化関数の出力を計算
def activation(self,X):
return self.net_input(X)
#1ステップ後のクラスラベルを返す
def predict(self,X):
return np.where(self.activation(X) >= 0.0,1,-1)
学習するデータセットはパーセプトロンと同じアヤメのデータセットを使います
# Irisデータセットの入手
import pandas as pd
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',header=None)
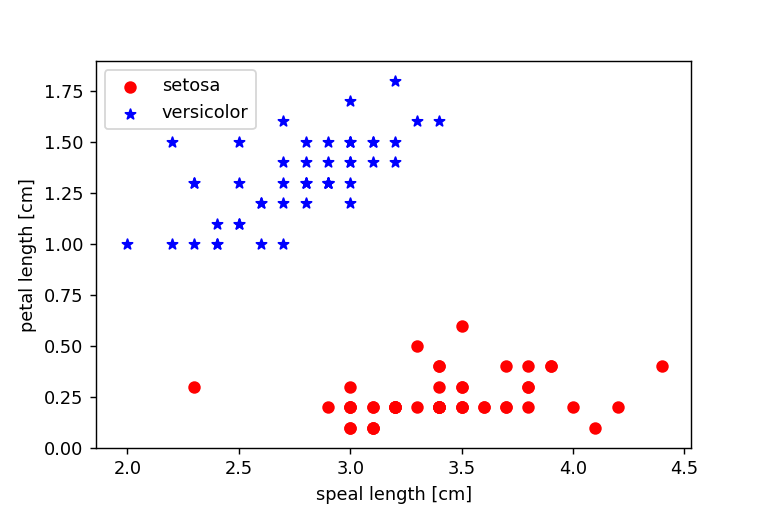
散布図を描画します
# グラフの描画
import matplotlib.pyplot as plt
# 1-100番目まで目的変数の抽出
y = df.iloc[0:100,4].values
# Iris-setosa を-1 iris-verginica を1に変換
y = np.where(y == 'Iris-setosa',-1,1)
# 1-100行目の1,3列めの抽出
X = df.iloc[0:100,[1,3]].values
# グラフのプロット
plt.scatter(X[:50,0],X[:50,1],color = 'red',marker = 'o',label = 'setosa')
plt.scatter(X[50:100,0],X[50:100,1],color = 'blue',marker = '*',label='versicolor')
# 軸ラベルの設定
plt.xlabel('speal length [cm]')
plt.ylabel('petal length [cm]')
plt.show()
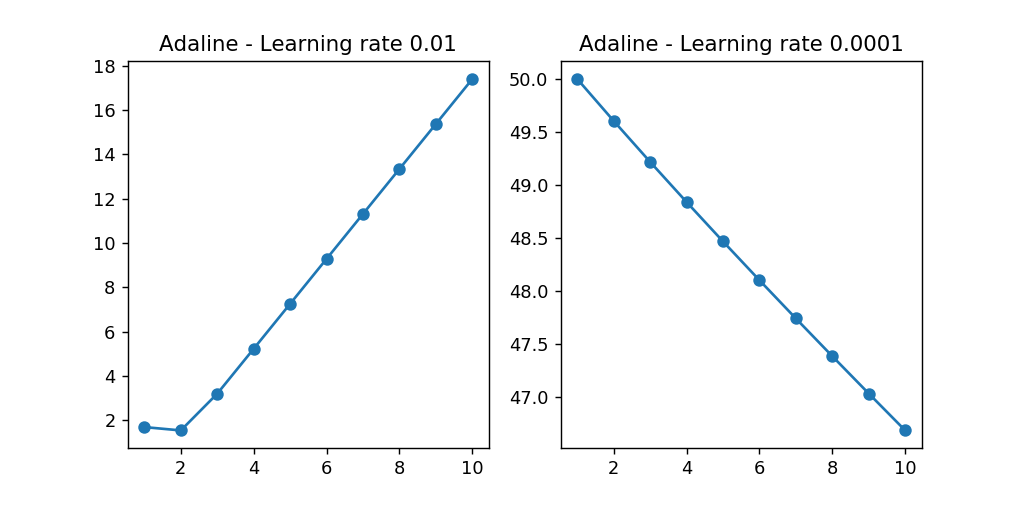
次に学習率$\eta$を 0.01 と 0.001 に設定してコスト関数とエポック数をプロットします
import matplotlib.pyplot as plt
# 描画領域を1行2列に変換
fig,ax = plt.subplots(nrows=1,ncols=2,figsize=(8,4))
# 勾配降下法によるAdaLineGDの学習
ada1 = AdalineGD(n_iter=10,eta=0.01).fit(X,y)
# エポック数とコストの関係を示す折れ線グラフのプロット
ax[0].plot(range(1,len(ada1.cost_)+1),np.log10(ada1.cost_),marker='o')
# 軸ラベルの設定
ax[0].set_xlabel=('Epochs')
ax[0].set_ylabel=('sum-squared-error')
# タイトルの設定
ax[0].set_title('Adaline - Learning rate 0.01')
# 勾配降下法によるAdaLineGDの学習
ada2 = AdalineGD(n_iter=10,eta=0.0001).fit(X,y)
# エポック数とコストの関係を示す折れ線グラフのプロット
ax[1].plot(range(1,len(ada2.cost_)+1),ada2.cost_,marker='o')
# 軸ラベルの設定
ax[1].set_xlabel=('Epochs')
ax[1].set_ylabel=('sum-squared-error')
# タイトルの設定
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.show()
ここで得られたグラフから、右のグラフでは学習率が大きすぎると誤差平方和が増加していることがわかるった。
左のグラフでは、学習率が非常に小さいので収束させるのに相当な数のエポック数が必要になることがわかった。
スケーリングをする
機械学習のアルゴリズムは、最適なパフォーマンスを実現するために何等かの特徴量スケーリングを必要とします。
今回は、標準化というスケーリング手法をとります。
標準化は、各特徴量を 0 として標準偏差を 1 にするというものです。
例えば、$j$番目の特徴量を標準化するには、サンプルの平均$\mu_j$をすべてのトレーニングサンプルから引いて、標準偏差$\sigma_j$で割ります。
x_j = \frac{x_j-\mu_j}{\sigma_j}
この場合に$x_j$はすべてのトレーニングサンプルの$j$番目の特徴量の値からなるベクトルです。
numpyのmeanメソッドとstdメソッドを使うと簡単に実装できます。
-
meanメソッド 平均を計算する
-
stdメソッド 標準偏差を計算する
# データのコピー
X_std = np.copy(X)
# 各列の標準化
X_std[:,0] = (X[:,0]-X[:,0].mean())/X[:,0].std()
X_std[:,1] = (X[:,1]-X[:,1].mean())/X[:,1].std()
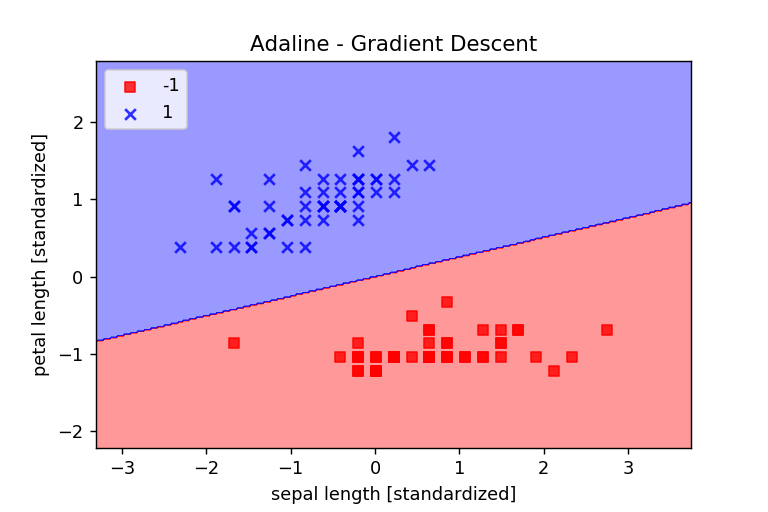
標準化の後に、学習率$\eta = 0.01$を使ってトレーニングして収束することを確認します。
from matplotlib.colors import ListedColormap
def plot_decision_regions(X,y,classifier,resolution = 0.02):
#マーカーとカラーマップの用意
markers = ('s','x','o','^','v')
colors = ('red','blue','lightgreen','gray','cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
#決定領域のプロット
x1_min,x1_max = X[:,0].min() - 1,X[:,0].max() + 1
x2_min,x2_max = X[:,1].min() - 1,X[:,1].max() + 1
#グリッドポイントの作成
xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
np.arange(x2_min,x2_max,resolution))
#特徴量を一次元配列に変換して予測を実行する
Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
#予測結果をグリッドポイントのデータサイズに変換
Z = Z.reshape(xx1.shape)
#グリッドポイントの等高線のプロット
plt.contourf(xx1,xx2,Z,alpha = 0.4,cmap = cmap)
#軸の範囲の設定
plt.xlim(xx1.min(),xx1.max())
plt.ylim(xx2.min(),xx2.max())
#クラスごとにサンプルをプロット
#matplotlibが1.5.0以下ならc = cmapをc=colors[idx]に変更
for idx,cl in enumerate(np.unique(y)):
plt.scatter(x=X[y==cl,0],y=X[y == cl,1],alpha=0.8,c = cmap(idx),marker=markers[idx],label=cl)
# 勾配降下法によるADALINEの学習(標準化後)
ada = AdalineGD(n_iter=15,eta=0.01)
# モデルの適合
ada.fit(X_std,y)
# 境界領域のプロット
plot_decision_regions(X_std,y,classifier=ada)
# タイトルの設定
plt.title('Adaline - Gradient Descent')
# 軸ラベルの設定
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
# 凡例の設定
plt.legend(loc = 'upper left')
# 保存先のファイル名(PNG形式)
fname = "gradient.png"
plt.savefig(fname, dpi = 128, tight_layout = True)
plt.show()
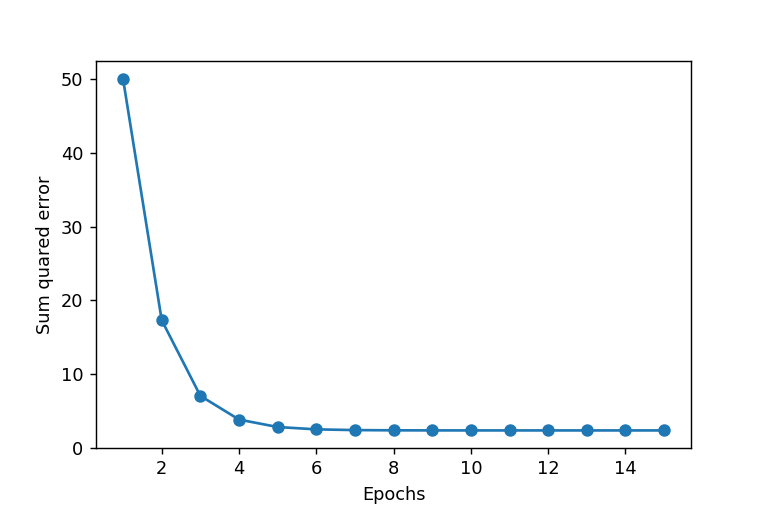
# エポック数とコストの関係性を示す折れ線グラフのプロット
plt.plot(range(1,len(ada.cost_) + 1),ada.cost_,marker='o')
# 軸ラベルの設定
plt.xlabel('Epochs')
plt.ylabel('Sum quared error')
# 保存先のファイル名(PNG形式)
fname = "sum_error.png"
plt.savefig(fname, dpi = 128, tight_layout = True)
plt.show()
グラフからわかったように、データの標準化をすることでADALINEが収束することが分かった。