はじめに
「Shadertoy はじめました - Qiita」の子記事です。My First Shader Sound (※音が出ます)を作った際にいろいろ気づいたトピックスを小さめの記事にしていきたいと思います。
この記事では、SphereTracingで形状を表現する距離関数(distance function)について考察します (残念ながら「解説」できるほど理解が深くないです)。iq氏によるリファレンスサンプルから一歩進んで、オリジナル形状の距離関数を定義したい人にとって理解の一助につながれば幸いです。
予め断っておくと、途中経過はそこそこ真面目に書きましたが、最後は不条理です。
六角柱の距離関数
iq氏によるリファレンスには「Hexagonal Prism」という六角柱の距離関数が示されています。
float sdHexPrism(vec3 p, vec2 h) {
vec3 q = abs(p);
return max(q.z-h.y,max((q.x*0.866025+q.y*0.5),q.y)-h.x);
}
計算自体は、q = abs(p) で絶対値をとって、q.z - h.y と q.x * 0.866025 + q.y * 0.5 - h.x と q.y - h.x の3式の最大値を返しています。
この距離関数は SphereTracing で凸形状を表現する典型的なやり方の一つだと思います。シンプルですが重要な性質が沢山詰まっています。
1. abs()
絶対値をとって第一象限だけ評価すれば xyz 各平面で対称に展開した形状の距離関数に展開できます。一軸だけ絶対値をとれば、その軸に垂直な平面に対して対称に展開できます。点との距離だけでレンダリングしてしまう SphereTracing ならではの重要な性質の一つです。
2. max()
最大値をとると形状の AND(論理積)合成ができます。「2つの形状までの距離を比較して遠い方を採用する」と考えれば理解の助けになるかもしれません。最小値は OR(論理和)合成になるので「距離を比較して近い方を採用する」とワンセットで考えるとより解り易い気がします。
3. 平面の合成
最大値評価している3式は、3つの平面までの距離を計算しています。つまり、この距離関数は 「3つの平面を AND 合成して xyz 平面に対象展開している」 事になります(平面の距離関数は非常にシンプルで SphereTracing でオリジナル形状を定義する際に最も基本的な図形の一つになりますが、この部分の解説は他に預けたいと思います)。
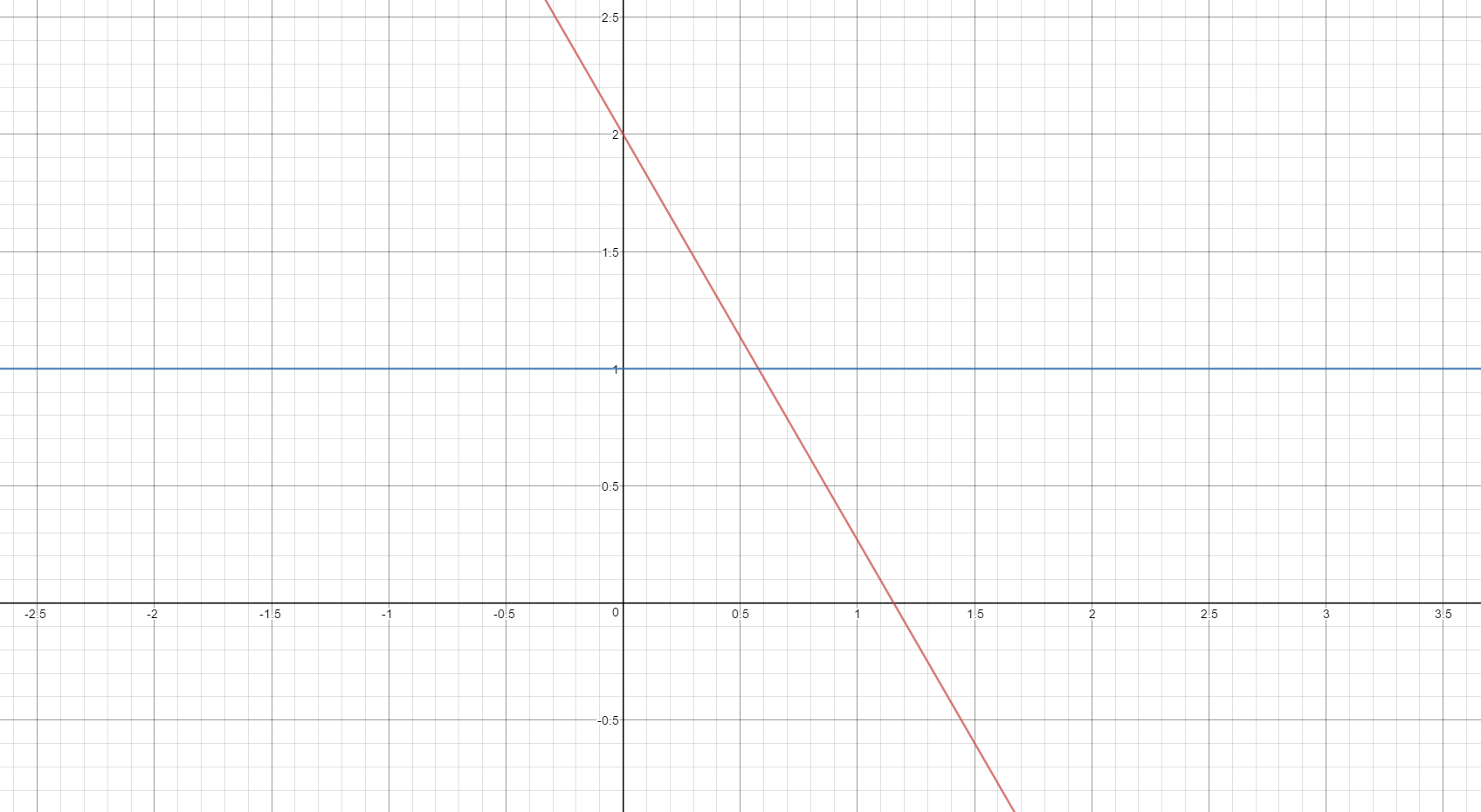
q.z - h.y と q.x * 0.866025 + q.y * 0.5 - h.x と q.y - h.x は(便宜上h.x=a, h.y=bとおいてます)、$$b=z$$ $$a=0.866025x+0.5y$$ $$a=y$$という条件で 距離=0 になりますから、表現したい平面は上記数式で表現されます。$a=0.866025x+0.5y$ と $a=y$ を $\{a=1\}$でプロットすると下のようになりますので、絶対値でx,y軸対称に展開すれば六角形=六角柱の側面になります。$b=z$ はそのまま z=b の xy 平面で角柱の上面と底面です。
https://www.desmos.com/calculator/pdlmnuedco
このように、実はSphereTracing では、形状を構成する平面を AND 合成するだけで、いかなる凸形状も表現することができます。頂点座標の計算も辺の計算も必要ありません! SphereTracing の漸近計算により、勝手に辺や頂点が求まってしまうのです。この性質により複雑な形状も非常に簡潔に表現できます。SphereTracingの優れた性質はたくさんありますが、その中でも突出した一つではないかと思います。
距離関数の角を丸める
比較的簡単に角を丸められるのも SphereTracing の大きな特徴の一つです。ポリゴンとは違いピクセル毎に正確に計算されるため、滑らかな曲面を表現できます。SphereTracing で角を丸める方法は(自分の知っている範囲では)以下の方法があります。
1. 辺に capsule などを配置して、AND 合成する。
AND 合成を簡単に行えるという特徴を生かした方法ですが、「辺の計算をしないで済む」という大きなメリットを潰してしまいます。
一方で、辺に配置する形状次第で、エッジだけ盛り上げたり、面取りをしたりと様々な加工が行えるため、辺情報が既知、または簡単に計算できる場合であれば、有用と言えそうです。
2. 平面同士を Smooth maximum 関数 で合成する。
Smooth maximum 関数(リンク先はSmooth minimum)は、隣接付近で徐々に変化する関数です。下グラフは、$y=smoothMin(x,2)$ 及び $y=smoothMax(x,4)$ をプロットしたものです。交差がなだらかな曲線になっているのがわかると思います。
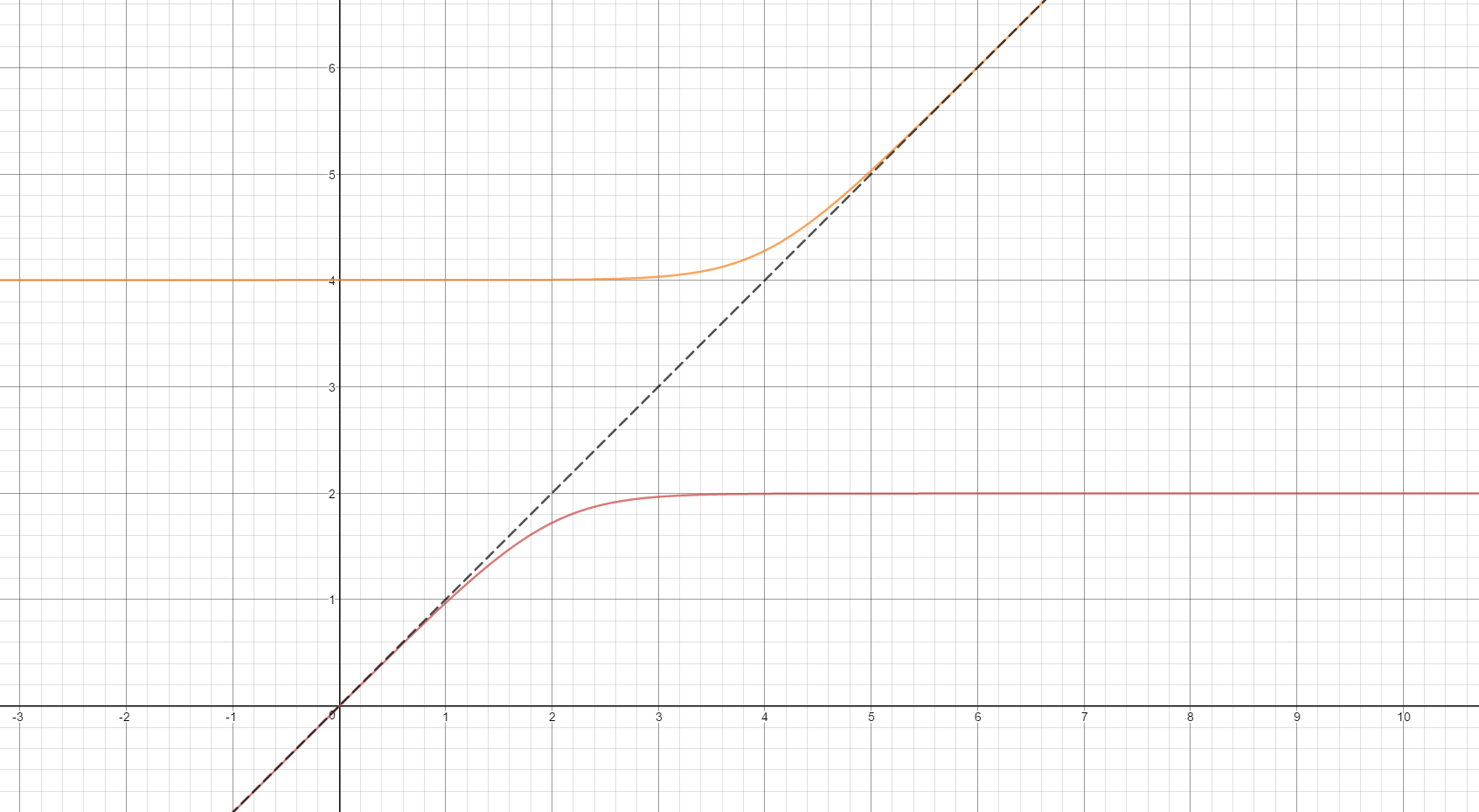
https://www.desmos.com/calculator/ulrl6to2fs
平面の合成で $max()$ の代わりに $smoothMax()$ を使うだけで、角が丸まります!
...と言いたいのですが、残念ながら今回の六角柱では少し面倒です。絶対値によるx軸対称展開を利用して角を作っているため、$smoothMax()$ を利用しても、この角が丸まりません。$smoothMax()$で丸めるには x 軸対称展開を諦めて、4平面のy軸対称展開 により六角柱側面を表現する必要があります。
この角丸め手法の威力は、Shadertoy はじめました week #2で遺憾なく発揮されていますので、こちらの記事で書こうと思います。
3. 角までの距離を求めて径を引き算する。
もし、角までの距離をちゃんと求めていれば、丸め径を引き算するだけで角が丸まります。典型的な例がiq氏によるリファレンスにも挙げられているRound Boxモデルです。
float udRoundBox( vec3 p, vec3 b, float r ) {
return length(max(abs(p)-b,0.0))-r;
}
距離関数の中でも一番美しい式だと思います。その洗練された算出方法に震撼しました。edo_m18氏の[GLSL] レイマーチング入門 vol.1:Boxの距離関数の理解で非常に詳しく考察されていますので、そちらを参考いただくのが良いかと思います。
この式は、box までの距離を求めて、最後に-rと径を引き算する事で角を丸めています。length(max(abs(p)-b,0.0))という数式は、角(辺)に対しても正確に box までの距離を算出しているため、引き算するだけで角が丸まります。
一方、今回の六角柱は平面の合成で形状を定義していますが、この方法はピクセル毎にどちらか遠い平面へのレンダリングをした結果として、境界線が現れているだけですので、角(辺)に対して正確な距離を計算していません。
角丸め六角柱の距離関数
以上を踏まえ、角丸め六角柱の距離関数を作りたいと思います。どの方法でも可能ですが、今回は3番を選択しました。
六角柱であれば、辺情報は簡単に算出できますので、1のやり方が一番良い気がしますが、今回は単に頭が丸まった六角柱が欲しいだけだったので、オーバースペックと考えました。
2番の方法であれば、頭が丸まった六角柱は、xy平面に並行な面の式だけ$smoothMax()$で合成する事で実現できます。よって合理的には2番を選択するべきだと思います。
3番を選択した理由は「やりたかったから」です。平面合成による凸形状表現が簡単なのは解っていたので、あくまでも角までの距離をきっちり計算した美しい関数を作りたかった(できたとは言っていない)。
float fHexpillar(vec3 p, vec2 h, float r) {
vec3 q = abs(p);
q.x = max(q.x * 0.866025 + q.z * 0.5, q.z);
return length(max(q.xy - h.xy, 0.0)) - r;
}
結果です。惨敗です。
一応 -r で角を丸めてはいるのですが、側面の数式が美しくもなんともない。一応解説を加えると、側面の2平面を合成して x に入れなおしてから、xyの2次元の四角形までの距離を計算することで角丸めを行っています。
感想
距離関数は非常にとっつきにくく、GLSLの世界は、湯婆婆も真っ青の名前省略地獄のため、正直、敷居は高いと感じます。ただ、SphereTracing は原理さえ理解してしまえば、他の手法ではきわめて複雑な事が、驚くほど簡単に表現できる事が判りました。いろいろな形状定義をしつつ、理解を掘り下げていければと思います。
