球面上でいろいろシミュレーションしたくなった。
たとえば、2次元平面上でシミュレーションするときには、ぼくらはよく周期境界条件という境界条件を課す。それは、こんなトーラス上で制限された運動を考えているのに等しい。
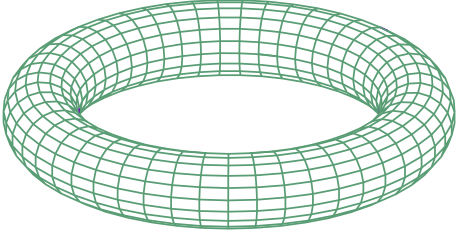
周期境界条件はお手軽なので、ついやっちゃうんだけども、
やっぱり球面上でやりたい。やりたいんだ。
球面上で微分方程式を解くためには球面を格子に切らないといけないのだけども、適当に3次元極座標表示を使うと北極と南極に格子点が密集する。
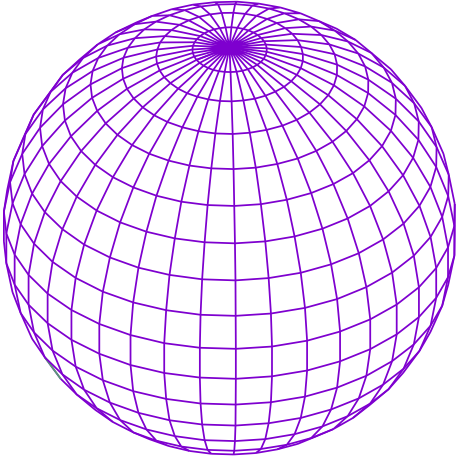
格子点が密集すると、その部分は格子幅が小さくなるわけで、
そのままつかっちゃうと方程式の安定条件に引っかかって計算が吹っ飛ぶ。
そこで、球面上を綺麗に分布するように点を打ち、その点を三角形でつなぐことで格子幅がだいたい同じになるような格子の切り方を考える。
この点の置き方が問題で、球面上でPoisson disk samplingとかやるのかなあ、めんどくさいなあ、、、と思っていたら、
スマートな点の置き方をやっている研究を教えてもらった。
http://cesdweb.aori.u-tokyo.ac.jp/~nicam/index.html
ベースとなるアイディアは、比較的簡単な多面体(正20面体)からスタートして、辺を細分化していくことで球に近づけていく、ということ。
アルゴリズムも簡単で、辺の中点を動径方向に球面に射影すればOK(だと思う)。
やってみるとすごく綺麗。

文献ではさらにスムージングをかけるらしいけど、エンジョイ勢のぼくにはこれで十分ではないかと思う。