Mission Designとしての深宇宙軌道設計

この記事は東京大学航空宇宙工学科/専攻 Advent Calender 2019の15日目の記事として書かれています.

はじめに

はじめまして. M1の@kdricemtです. 現在は小型衛星を開発している某研究室に所属しています.
弊学科ではシステムコースに進むと軌道力学の講義がB3にあるのですが, 去年まで¹は実際に演習で軌道設計を行うわけではなかったのであの講義がどの様に実際の軌道設計につながっているのか,　正直あまり掴めないまま卒業する方も多いのではないかと思っています. 別に軌道なんて結局最終目的地に到着できれば何でもいいのでは? と思っている方もいるかもしれません.

宇宙機の研究室に入って1年半が過ぎ, 深宇宙探査機の軌道設計が実際どの様に行われているのかについての全体像が最近少しずつ見えてきた気がするので, そこら辺の内容を紹介して軌道設計に興味を持ってもらえたら嬉しいな, と思い今回の記事を書きました. 一応航空のアドベントカレンダーの記事ということで, 多少専門的な内容を含んだ内容となっています.

深宇宙ミッションにおける軌道設計の立ち位置

軌道設計そのものについて書く前に, そもそも何故軌道設計が深宇宙ミッションにとって重要な作業なのかについてミッション全体の進め方の観点から書きたいと思います. しばしお付き合い下さい...

そもそも深宇宙ミッションとは?

深宇宙ミッションとは, 深宇宙探査機を飛ばすミッションです. 深宇宙探査機とは, 一般には地球の重力圏を離れて違う惑星や小惑星の探査を行う人工衛星を指します. 月探査衛星が「深宇宙」に含まれるかどうかは諸説ある気がしますが, 今回は月へ向かう衛星も含めることにします. 通信衛星や気象衛星, 偵察衛星など商用・軍用衛星が多く打ちあがっている地球周回衛星とは異なり, ほぼ全ての深宇宙探査機は科学探査目的, もしくは将来の科学探査ミッションのための工学実証目的で打ち上げられています. おそらく日本で一番有名な深宇宙探査機「はやぶさ」は一見サイエンスミッションに見えますが, 実はMUSESシリーズという工学技術実証ミッションだったりします.

深宇宙ミッションの概念設計(初期検討)の流れ

このような深宇宙探査機の初期検討はどのように勧められるのでしょうか? トップダウンで決まる一部のミッションは勝手が違うかもしれませんが, 一般的に深宇宙ミッションはある打ち上げ機会 (ロケット) が与えられて, それに対するミッション案を公募で募り, 審査を勝ち抜いたものが実行に移されるという場合が多いです. 公募が出されたら, まずはサイエンスの研究者とエンジニアでチームを組んで興味深い探査目標とその形式を決め, そこから軌道への要求が決まります. フライバイ探査なのか, 天体の周りを周回するOrbiterによる探査なのか, 複数機を使ったSwarmによる近接フライバイ探査なのか, などです.

スイングバイ探査ミッションのレジェンド, [ボイジャー2](https://ja.wikipedia.org/wiki/%E3%83%9C%E3%82%A4%E3%82%B8%E3%83%A3%E3%83%BC%E8%A8%88%E7%94%BB)

目標が決まったら, 本当にそのミッションがフィージブルであるかどうか検証しなくてはいけませんが, そのためにまず行うのは軌道設計です. まず軌道チームで簡易的な軌道計算を行い, 必要なロケットの打ち上げエネルギー($C_3$と呼びます)と深宇宙$\Delta V$ (宇宙機が推進剤を消費して獲得しなければならない増速) をなるべく少なくできそうな軌道を作ります. そうすると, $C_3$からロケットが打ち上げ可能なペイロードの量が, 深宇宙$\Delta V$とツィオルコフスキーの公式
$$\Delta V = I_{sp} g ln\frac{m_0}{m_T}$$
から衛星のドライマス (燃料を除いた質量) が見積もれます. さらに大まかな軌道が与えられていれば, バスシステム設計チーム (システムチームと呼ばれることが多い)側で, 地球, 太陽, 探査機の位置関係から熱計算, 電力計算, 通信回線計算等の解析を行うことができるようになるので, 必要条件を満たした上で衛星全体重量が計算したドライマスに収まるかどうかを確認することができます. これで, 全体的にフィージビリティーのあるミッションかどうかの検討はつけることができます.
フィージビリティーの確認が取れたら, システムチームと軌道設計チームが相互にやり取りしながら, ループを回して設計を詳細化していきます. このようにしてProposalへと備えていくのです. 無事Proposalが採択されれば, 実際の開発が始まります.

結局何で軌道設計は重要なの?

宇宙研の先生のお言葉を引用させていただきます.

軌道を設計すると、打上げ時期や、目標天体への到着時期、つまり探査計画の主要スケジュールが決まります。これは探査の実施を決定するに当たっての重要な情報になります。また、軌道を設計すると、打上げロケットに要求される打上げエネルギーや、目標天体に到着するまでに必要な推進薬量が決まります。これらは探査機の規模を決める重要な設計要素になります。また、軌道を設計すると、航行中の探査機と太陽・地球との距離、探査機から見た太陽・地球・目標天体との位置関係が決まります。これらは探査機の電力、熱、通信、機器配置について重要な設計条件を与えます。つまり、軌道設計とは、単に宇宙に線を描くというだけの作業ではなく、さまざまなことを考慮に入れて、探査計画・ミッションを創り上げていく重要な作業なのです。このことから、軌道設計の作業は、しばしば「ミッション設計」とも呼ばれます。

ミッション設計という言葉は, なんかミッション全体を動かしているような印象を与える言葉ですよね

• 軌道設計が深宇宙ミッションの概念設計の起点となること
• 深宇宙ミッションでは軌道設計とバスシステム設計の間のカップリングが多数存在し両者を切り離して設計を行うことが難しいため, 軌道設計はミッション検討の最初から最後まで続く作業であること

以上の2つが, 他のサブシステム設計とは異なる, 軌道設計の特殊な立ち位置につながっていると言えるのではないでしょうか.

「ミッション設計」のプロセス

長々と深宇宙ミッションにおける軌道設計=ミッション設計の重要性について語ってしまいましたが, いよいよ本題である軌道設計の一般的なプロセスについて, 現在どの様なことがホットなテーマとして研究されているかについての雑談を交えつつ, 紹介して行きたいと思います.

1: 大まかなシーケンスを決める

まずは, ロケットの打ち上げ性能と最低限必要なドライマスの目安, 探査目標までの必要エネルギーから探査目標に至るまでの大まかな作戦を決めます. ここは過去のミッション実績や軌道設計屋の知識や経験をベースにして行われるため, 引き出しの多さが求められるところです. 長年軌道設計を行っている専門家は, どのようなことを行うとどのくらい宇宙機の運動エネルギーを獲得できるかが頭に入っているそうです.
いくつかの例を簡単に紹介したいと思います. (多少専門的な内容なので, 軽く読み流してもらって大丈夫です..)

例1: 土星Orbiter Mission (Ex: Cassini)

Cassiniは1997年に打ち上げられたNASAとESA共同開発の土星探査機です. タイタンに降下したホイヘンス (ホイヘンスの開発を担当したのはESA) がメタンの湖を捉えたり, カッシーニ自体もエンケラドスをフライバイして南極付近から噴出するプルームの存在を明らかにするなど, 多くの歴史的な発見をもたらしました. カッシーニの発見にインスパイアされて, 深宇宙探査に魅せられた少年少女も多いと思います. 僕もその一人なのですが...
Cassiniのようなミッションの軌道設計を行うことになったら, 例えば以下のようなことを真っ先に考えると思います.

• 大量のミッション機器を土星圏まで運ぶためには多くの燃料が必要. ミッション期間を引き換えにしても, スイングバイ²を繰り返してできる限り必要な増速を減らして, 土星圏に運べるミッション機器の重量を増やしたい.
• Delta-VEGA³がスタンダードかな. それでもエネルギー的に足りなければ, 金星スイングバイを入れる.
• Insertionに大きな$\Delta V$ が必要だし, ミッション期間も長いから電気推進より化学推進が適当そう...
• 位相が合えば木星スイングバイを使いたい...火星は使えたらラッキーだけどスイングバイしても増速はそこまで得られないし, 旨味はあまりない
• 土星重力圏にInsertionしたあとは土星衛星をフライバイしながら徐々に土星(木星)に対する速度を落として, 土星近くの衛星 (エンケラドスなど) のフライバイ探査を行う

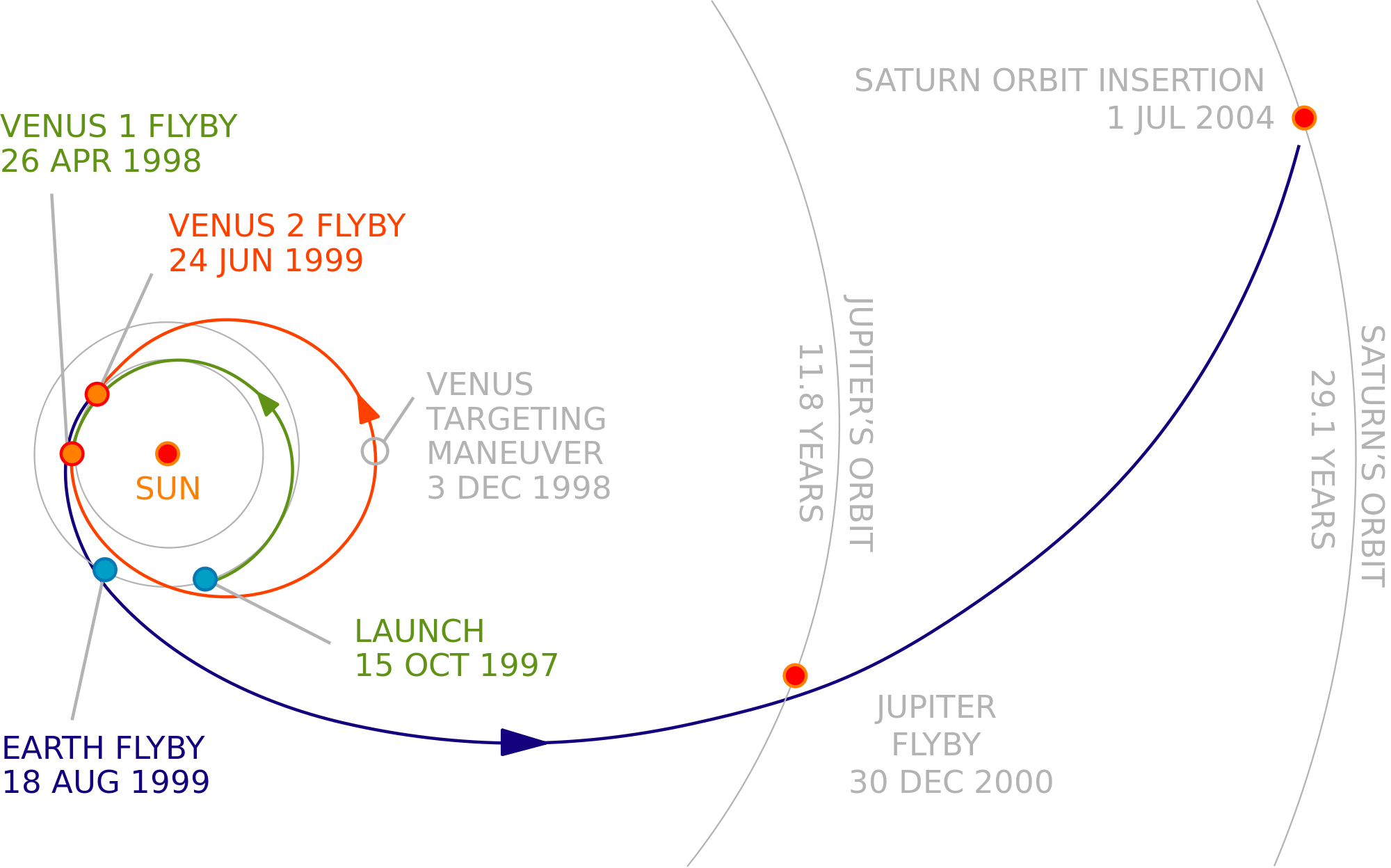
[上図] Cassiniの惑星間遷移軌道

Cassiniの様な外惑星探査ミッションでは熱や通信などシステム側の設計も非常にタイトになるので, 軌道とシステムを同時に考えた総合的な探査機設計を意識することが非常に重要になります...

例2: 小型衛星による月探査ミッション (Ex: EQUULEUS)

EQUULEUSは東大の中須賀・船瀬研究室とISASで共同で開発している6U (10cm x 20cm x 30cm) の超小型衛星です. 最終的には月の裏側のハロー軌道⁴と呼ばれる軌道に投入され, 月の裏側の月面衝突閃光の撮像を狙います. EQUULEUSのような小型衛星によるハロー軌道投入ミッションを考える上では, (円)制限三体問題のダイナミクスに関する知識が不可欠です.

[上図] L2 Halo 軌道のFamily. 閉じた青い軌道一つ一つが独立したハロー軌道で, 比が書いてある赤い軌道はSynodic Halo Orbitと呼ばれる太陽との位置関係が元に戻る周期が軌道周期と整数比の関係にある特殊なハロー軌道.

例えば以下のようなことを考えていきます.

• 超小型衛星であるため達成可能な増速(減速)量が限られており, ロケットから放出後燃料を吹いて探査軌道へと向かい, 到着後再び推進剤を吹いて減速するというようなシンプルな方法 (Direct Transferと呼ばれる) で軌道に投入することはできない...→Low Energy Tranfer⁵を使って, 太陽の潮汐力を使ってエネルギーを獲得する.
• Low Energy Transferで足りない分のエネルギーは, 月スイングバイで補う.

月フライバイを加えたLow Energy Transferの様子を太陽と地球の位置を固定した回転座標系で書いてあげたのが, 下の図 (Bing-Wei, 2018, [1]) です. 地球から離れた位置で太陽の潮汐力を受けて軌道がググッと曲げられているのがわかると思います. このような軌道を使用することで, 非常に少ない燃料で探査機をハロー軌道まで持っていけるのがLow Energy Transferと呼ばれる手法です.

ラグランジュ点周りの周期軌道を利用するミッションや月ミッションなど, 三体問題の枠組みで行う軌道設計は非線形力学やカオス理論に対する深い理解が必要になる場合も多くあり, 現在でも盛んに研究されています. (筆者はきちんと勉強できていないです) 三体問題の軌道設計について詳しく知りたい方は, 参考文献[2]などを読んでみるといいかもしれません. 専門的で難しいですが...

2: Initial Guess 軌道の作成

全ての天体から受ける重力や諸々の摂動, 制約条件等を考慮して必要燃料を最小化する軌道最適化問題は, 非常に多くの局所解の存在する複雑な非線形最適化問題です. 妥当な(局所) 最適解に収束させるためには, 非線形最適化ソルバーに適切な初期解を渡してあげる必要があります. そこで, 2体問題や制限3体問題等の簡易的なダイナミクスを仮定してあげて, ランベール問題の解をプロットしたPorkchop図やTisserand図の活用, Invariant Manifold, Week Stability Boundary など様々な「技」を組み合わせて解空間を広く探索しながらその特徴を見極め, 最終的に適切な初期予想解を作りあげる(見つけ出す)のがこのステップになります. 1と並んで, 軌道設計を行う人の力量が最も問われるフェーズです.

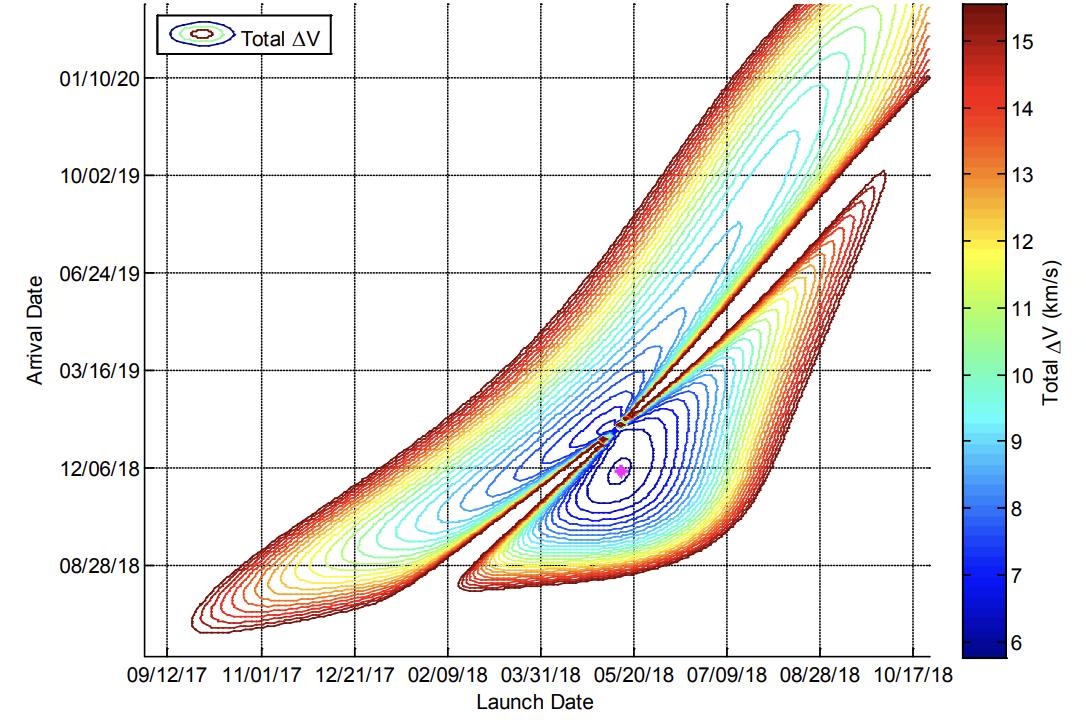[上図] 地球-火星遷移軌道のPorkChop図 (参考文献[3]より引用). このような図を作ってあげげて, 出発時刻と到着時刻を振ってLambert問題を解いてあげることで, 燃料消費が少なく火星へと遷移できる時期を探すことができる.

現在1,2のプロセスを進めるためには専門家の手を借りる必要があります. しかしながらしっかりとした軌道設計のノウハウを持っている人は限られているので, 今後探査機の小型化が進み深宇宙探査機を飛ばせる機会が増えていっても, 軌道設計がネックとなって中々新規ミッションの概念設計を進められなくなることが十分に考えられます. そこで, 遺伝的アルゴリズム, 木探索, 強化学習などを使って, シーケンス決めからInitial Guessまでのプロセスの全体あるいは一部を自動化してしまおうという研究が特に2010年代から盛んに行われています. まだ実ミッションにそのまま使える様なレベルのツールはないのですが, 将棋AIやゲームAIの近年の急激な性能上昇を見ていると, 個人的には5-10年後くらいには軌道生成プロセスが完全自動化されていてもおかしくはないと思っています. ではそれで軌道設計を行ってきた人の仕事がなくなってしまうかというと, 後述する軌道設計のミッション設計的な側面を考えればそうはならないと思いますが...

3. 軌道最適化

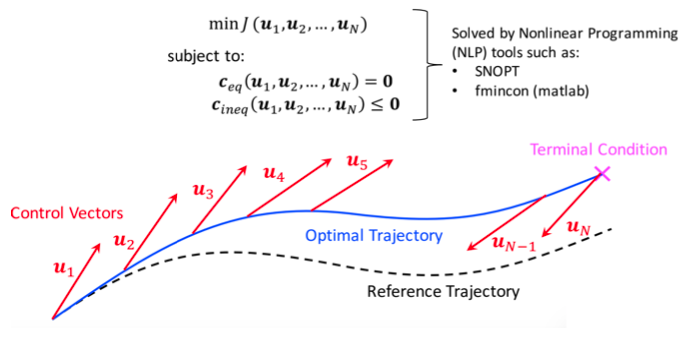
一旦良いInitial Guess Trajectoryができてしまえば, あとは多様な天体から受ける重力や外乱の効果を考慮したより高精度なダイナミクスモデルできちんと軌道が滑らかに繋がって, 消費燃料を最小化できるように最適化をかけるだけです. ここで「だけ」と書いてしまったのは, 現在この最適化部分については比較的ロバストに解を収束させることのできるソルバーが各国の宇宙機関を中心として既に開発・公開されており (ex: PyKEP,PyGMO), これらのツールを利用する方法を習得してしまえば, 最適化を実行するのは軌道設計の内最も困難な部分ではなくなってきているためです. もちろん誰でもできるというわけではなく,ソルバーの出した解が本当に最適な解となっているかどうかを判断したり, 解が収束しない際にどのように対処するかを判断するためには, Primer Vector Theory⁶ などをはじめとして最適制御や軌道力学, 軌道最適化の基礎をきちんと理解している必要があります.

軌道最適化の手法を分類すると (MetaHeuristics的な手法を除けば) 大きく直接法, 間接法, 動的計画法の3種類があります. 連続時間最適制御問題における変数を離散化して非線形計画問題 (Nonlinar Programming)に帰着するのが直接法 (Direct Method), ラグランジュ乗数を導入して状態量とラグランジュ乗数についての2点境界値問題に帰着するのが間接法 (Indirect Method), ハミルトン・ヤコビ・ベルマン方程式を逆方向に解いていくのが動的計画法 (Dynamic Programming) です. それぞれ長所と短所がありますが, 計算機の演算能力が向上して大規模なスパース行列の演算ができるソルバー ⁷ が出てきたことや, 収束性が間接法に比べて良いことからMutiple Direct Shooting などの直接法を用いる最適化ライブラリが多いです.

Direct Shooting法のイメージ

もちろんこの最適化自体に対する研究も今も盛んに行われています. 最近はただ単に最適化をするのではなく, スラスターの誤差や探査機の観測(軌道決定)の誤差, さらには推進系の故障に対してロバストな軌道を得るための最適化手法などが研究されています.

軌道最適化に興味のある人は, 参考文献[4],[5]あたりが入門書として読みやすいのではないかと思います.

4: PostProcessing & 衛星システム設計とのイタレーション

無事最適化が収束して良さそうな解析解 (燃料最小解など) が得られても, 軌道設計は終わりではありません. でき上がった軌道が本当に探査機のシステム設計側から来る要求 (制約) を満たしているかどうか, 各種ミッション解析をして検討する必要があります. 例えば, 探査機の熱設計は成立するか, 探査機が経験する蝕を耐えるだけのバッテリー容量が探査機にあるか, サイエンスで欲しいデータは本当に得られるのか, などなど. また軌道が固まってきたら, マニューバの前の軌道決定⁸はどのタイミングで行うのか, マニューバの誤差はどのようにして吸収するのか等, 運用シナリオを考慮して軌道が成立するかを考えなくてはなりません.

必要燃料を最小化する「最適」な軌道は設計したし, あとはシステム設計側で何とかしてよと思いたくなってしまうかもしれません. しかし予期せぬ不具合や大人の事情によってシステムチームが設計変更を強いられ, 軌道に課せられる制約が変わることはよくありますし, 検討を詳細化していくと, 設計した軌道が運用の際の制約を満たせそうにないことや, 燃料消費最小化だけ考える分には最適な軌道が実はシステム設計を考慮に入れると全体重量を最小にできる軌道ではなかったことが判明することも十分起こりえます. そのため, 衛星システム設計, 運用計画作成, 軌道設計の間でのイタレーションを行いながら, 最終的な探査機, 運用計画, 軌道計画が出来上がっていくのですが, これこそが深宇宙軌道設計=深宇宙ミッション設計の面白さなのではないかなと私は考えています. 深宇宙という極限環境を乗り越えてフロンティアを切り拓くべく, チーム全員の連携で設計を突き詰めていく深宇宙ミッションはまさに究極の統合設計最適化プロセスなのです！

最後に

軌道設計が深宇宙ミッションの検討において果たしている役割や, その進め方などを紹介しました. 大きなテーマの記事を書いてしまいましたが, 筆者は宇宙期間等で軌道設計を専門に行っている研究者ではない上に経験も浅いので, 要点を外している箇所や誤り等があるかもしれません. お気づきの方がいたら指摘していただければと思います.
また初めての記事執筆で慣れないこともあり, 少し要点の掴みづらい記事になってしまったかもしれません. 深宇宙ミッションの検討って何か面白そうと思っていただけたら, この記事の目的は大体達成できたかなと思います. (もちろん同志が増えればさらに嬉しいです!)
機会と需要があれば, 今後はより細かいTopicについて個人的にまとめている内容などもソースコードとともに記事にできたらいいなと思っています.

参考文献

[1] Bing-Wei, L.,et al. "Low-energy Lunar Trajectories with Lunar Flybys", Chinese Astronomy and Astrophysics, 43, 575-593, 2018
[2] Koon, W.S, et al. "Dynamical Systems, the Three-Body Problem and Space Mission Design", 2011
[3] Wolley,R.C. et al. "On the Nature of Earth-Mars Porkchop Plots",AAS,2013
[4] Betts, J.T. "Survey of Numerical Methods for Trajectory Optimization". Journal of Guidance, Control, and Dynamics, 21(2), 193-207, 1998
[5] 大塚敏之 「非線形最適制御入門」コロナ社, 2011
[6] Conway, B.A. "Spacecraft Trajectory Optimization", Cambridge University Press, 2010

1. 実は昨年末, 三年生の軌道力学の講義をコーディングを含むレポートベースにしてはどうかと何気なく進言した所, 本当にそうなってしまいました... ↩

2. Swing-by, Flyby, Gravity Assist. 探査機が惑星の近傍を通過するときに惑星の重量によって惑星との相対速度が保たれたまま軌道が曲げられることを利用して, 探査機を増速させる(もしくは減速させる)方法. 燃料をほぼ消費することなく探査機の速度を大きく変えることができるため, スイングバイをうまく使用することで軌道設計の自由度を大きく向上させることが可能となる. ↩

3. Delta-V Earth Gravity Assist. 一回地球とのresonant orbit (軌道周期が地球の公転周期と整数比の関係がある軌道) に入れて, 遠点でマニューバを入れて地球との再会合時の相対速度を上げたのち地球スイングバイをすることで大きな増速を得る手法. もちろん地球以外の天体でも同様の手法を使うことができ, 手法自体は一般的にV-Infinity Leveraging Transfer (VILT) と呼ばれている. (Cassiniの軌道図のオレンジの部分は金星-金星VILT) ↩

4. L1, L2点のラグランジュ点の周りを周回する周期軌道. 月の近くにある縦に大きな楕円を描く形をしている. 比較的安定で少ない燃料で衛星を軌道に留めておけることから, L2のハロー軌道は月の裏側への中継衛星や, 新しい月周回ステーション (LOP-G)の停留場所として注目されている. ↩

5. 太陽-地球-探査機の制限三体問題の枠組みで定義される安定・不安定多様体と, 地球-月-探査機の制限三体問題の枠組みで定義される安定多様体をつなぎ合わせて作られる遷移軌道. 太陽からの潮汐力を受けて加速することで, 少ない出発エネルギーで月に到達することが可能となり, さらにほぼ燃料を使用することなくハロー軌道やリアプノフ軌道への投入が可能となる. ↩

6. D.F.Lawdenによる軌道最適化の初期の研究の成果. 1次の必要条件を満たす解について, Primer Vectorと呼ばれるベクトルを用いることで最適制御入力を表現することができるとした定理. 詳細は参考文献[6]を参照. ↩

7. SNOPTなど ↩

8. 地球上の基地局と探査機の間で通信する際の電波の伝播時間やドップラーシフト量のデータを利用して, 衛星の軌道を推定すること. ↩