はじめに
こんにちは。みなさんは、データにモデルを当てはめたとき、その良し悪しをどのように評価していますか?とりあえずMSEや尤度などを使うことがほとんどでしょうか。最近、非線形モデルを用いた分析に決定係数が使われていた例を見かけたのですが、そもそも非線形モデルで決定係数を用いるのは適切なのでしょうか?このことが気になったので整理してみました。すでに同様の問題を指摘している記事がありますので、そちらも併せて参照してください。
決定係数とは
決定係数は分析ソフトなどでいわゆる$R^2$と示され、推定された回帰式のデータに対するあてはまりの良さを表します。誤差やAICなどと並べて回帰分析の結果などに表示されます(Rではlm()で回帰分析した結果をsummary()で表示すると、Pythonではstatsmodelsライブラリを使って回帰分析を行い.summary()メソッドで$R^2$が表示されます)。0から1の間の値をとり、モデルがどのくらいデータの変動を説明できているかを表す指標などとよく説明されます。データを$(x_i, y_i)$、$i$番目の$y$の予測値を$\hat{y_i}$、$y$の平均値を$\bar{y}$としたとき決定係数は
R^2=1-\frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{\sum_{i=1}^n(y_i - \bar{y})^2}
によって計算されます。
導出
決定係数を理解するためには次の3つの項が重要となります。
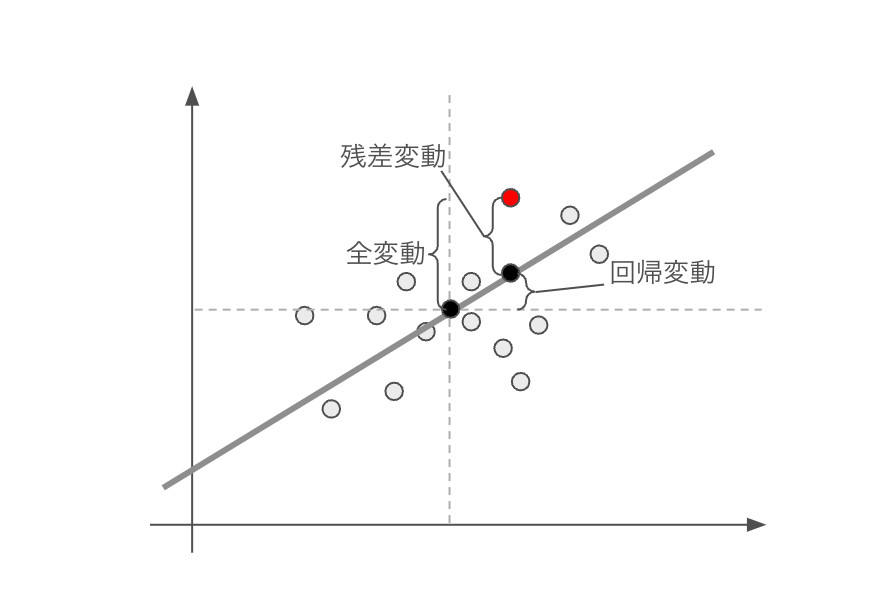
- 全変動:データの平均値からの偏差
- 回帰変動:回帰予測値のデータ平均からの偏差
- 残差変動;データの回帰予測値からの偏差
これら3つの量の関係を図示したのが、以下の図です(この図はこちらの記事を参考に作成しました)。二つの波線の交点がデータの平均値、グレーの太線が回帰直線を表し、それらをもとに全変動、回帰変動、残差変動に対応する部分が示されています。
まず、全変動を以下のように式変形していきます(※以下、総和は適宜データ数で和をとります)。
\begin{align}
\begin{split}
\sum(y_i-\bar{y})^2 &=\sum((\hat{y_i}-\bar{y})+(y_i-\hat{y_i}))^2 \\
&=\sum((\hat{y_i}-\bar{y})^2+(y_i-\hat{y_i})^2 + 2(\hat{y_i}-\bar{y})(y_i-\hat{y_i})) \\
\end{split}
\end{align}
ここで、$2\sum(\hat{y_i}-\bar{y})(y_i-\hat{y_i})$について$\hat{y_i}=\bar{y}+\beta_1(x_i-\bar{x})$と$\beta_1=\frac{\sum(y_i-\bar{y})(x_i-\bar{x})}{(x_i-\bar{x})^2}$表されることから
\begin{align}
\begin{split}
2\sum(\hat{y_i}-\bar{y})(y_i-\hat{y_i})&=2\sum(\bar{y}+\beta_1(x_i-\bar{x})-\bar{y})(y_i-\bar{y}-\beta_1(x_i-\bar{x})) \\
&=2\sum(\beta_1(x_i-\bar{x}))(y_i-\bar{y}-\beta_1(x_i-\bar{x})) \\
&=2\beta_1\sum(x_i-\bar{x})(y_i-\bar{y}) -2\beta_1^2\sum(x_i-\bar{x})^2 \\
&=0
\end{split}
\end{align}
となります。このことより、式(1)は
\begin{align}
\begin{split}
\sum(y_i-\bar{y})^2
&=\sum(\hat{y_i}-\bar{y})^2+\sum(y_i-\hat{y_i})^2
\end{split}
\end{align}
となり、全変動が回帰変動と残差変動の和で表わされることがわかります。ここで、回帰式の当てはまりの良さとして全変動に対する回帰変動の割合という量を考えてみると式(3)より
\begin{align}
\begin{split}
\frac{\sum(\hat{y_i}-\bar{y})^2}{\sum(y_i-\bar{y})^2}
= 1 - \frac{\sum(y_i-\hat{y_i})^2}{\sum(y_i-\bar{y})^2}
\end{split}
=R^2
\end{align}
となり、冒頭で示した決定係数の計算式が得られます。さて、ここまで述べてきた導出について振り返ってみると、式(2)の変形の過程でモデルが線形であることを用いています。つまり、決定係数が線形モデルを前提としていることがわかります(非線形モデルでも決定係数の値自体は計算できてしまいます)。
決定係数と相関係数
決定係数は相関係数の二乗と説明されることがあります。ついでに、こちらも確認してみましょう。モデルが直線であるとき、$\hat{y_i}=\beta_1 x_i + \beta_0$と$\beta_1=\frac{Cov(X, Y)}{\sigma_X^2}$がなりたつので
\begin{align}\begin{split}
R^2&=\frac{\sum(\hat{y_i}-\bar{y})^2}{\sum(y_i-\bar{y})^2}\\
&=\frac{\sum((\beta_1x_i+\beta_0)-(\beta_1\bar{x}+\beta_0))^2}{n\sigma_Y^2}\\
&=\beta_1^2\frac{\sum(x_i-\bar{x})^2}{n\sigma_Y^2}\\
&=\frac{Cov(X,Y)^2}{n\sigma_Y^2 \sigma_X^4}n\sigma_X^2\\
&=\frac{Cov(X,Y)^2}{\sigma_X^2 \sigma_Y^2}
\end{split}\end{align}
と相関係数の二乗になります。
最後に
本稿では、使用しているモデルが線形モデルである場合に、決定係数がどのように意味を持つのかを確認しました。分析ツールによっては、特に深い意図なく表示されていることが多いのかもしれません。決定係数の背後にある仮定を理解した上で使いつつも、MSEなど他の指標を併せて提示する方が無難だと思います。