先日ARKitのための3D数学という記事を書きました。その中でも言及していますが、今記事では、transformを理解するために、4*4行列だけにフォーカスして説明していこうと思います。
僕も最初はよくわかっていませんでした。しかし今では理解できていて、座標変換するときに4*4行列を使うことの便利さを痛感しています。
4*4行列とはなんなのか

行列です。
この行列をベクトルに掛けると、座標を変換することができます。
こんなかんじの行列のイメージだけまずは覚えてください。
3D座標系を理解しよう
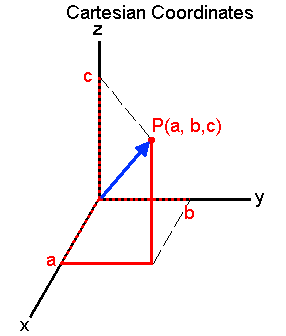
3D空間上にx軸とy軸とz軸があって、その空間上の点が(x, y, z)という座標系で表されることは中学高校の数学をやっていれば理解できるでしょう。
以下の図では、xがaで, yがbで, zがcで示される点Pを表しています。
しかし、座標変換を考えるときに、この点だけを考えるのは得策ではありません。
ベクトルで考えるのがオススメです。
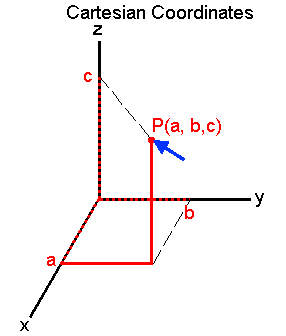
点Pをベクトルで考える
点Pをベクトルで表現してみました。
原点から点Pに伸びる矢印です。
点Pだけではベクトルを表現できません。なぜなら原点から伸びる矢印じゃなくて、別のところから矢印を伸ばすことで別の大きさ、向きのベクトルを作ることができるからです。
以下みたいな感じ。
ベクトルは点ではなく、向きと大きさを含んだ矢印です。
オブジェクトで考えてみよう
次に以下のようなポットを考えてみましょう。

ポットを囲む六面体は先ほど紹介したベクトルを使って考えることができます。
以下のイメージです。OとPが決まれば六面体が確定できるのでその六面体の中にあるポットの向きと大きさを定義することができます。

では、4*4行列の話に戻ります。
ここで4*4行列をみてみよう

ポットのベクトルの**向き(回転)と大きさ(拡大縮小)**は、この行列の赤で囲まれた部分を使って変換できます。
拡大縮小
| オリジナル | 大きさ2倍 |
|---|---|
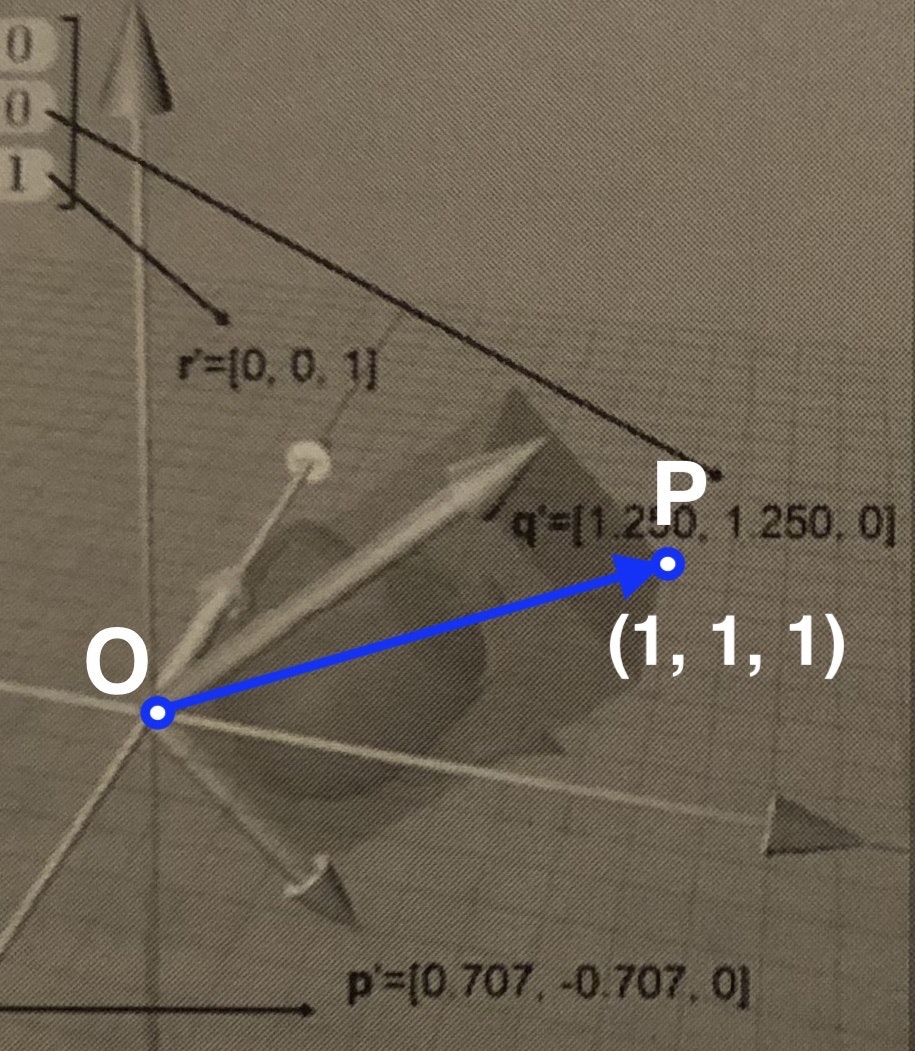 |
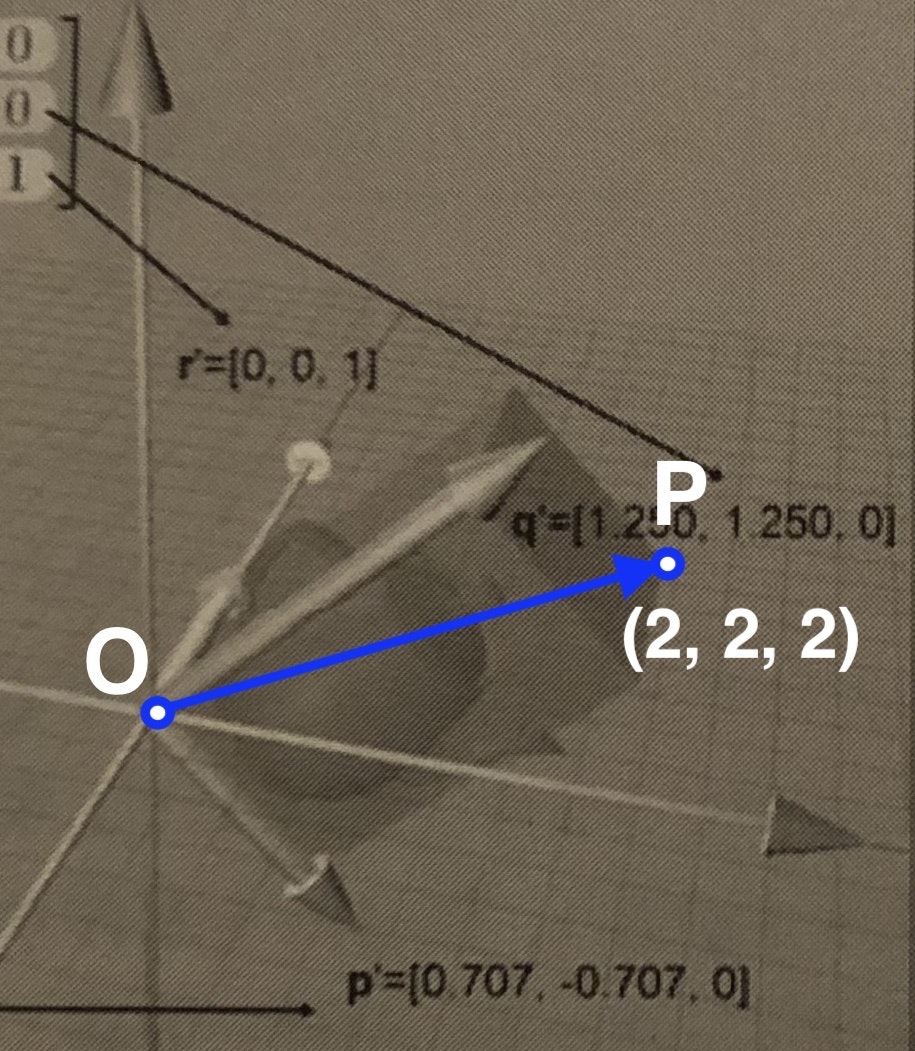 |

ベクトルが拡大しましたね。
この左にある44行列が、2倍の拡大を表す44行列です。
回転
次に、このポットをz軸を中心に30度回転させるケースを考えてみましょう。


ベクトルが回転しましたね。
x、y、z軸を中心に回転する時の行列は決まっているので、わからなければ都度確認すればいいと思います。https://ja.wikipedia.org/wiki/%E5%9B%9E%E8%BB%A2%E8%A1%8C%E5%88%97
そして、iOS開発においてはSceneKitのAPIで作れるので心配はいりません。ARCore Sceneformでも作れるし、c++にもあります。覚える必要はありません。
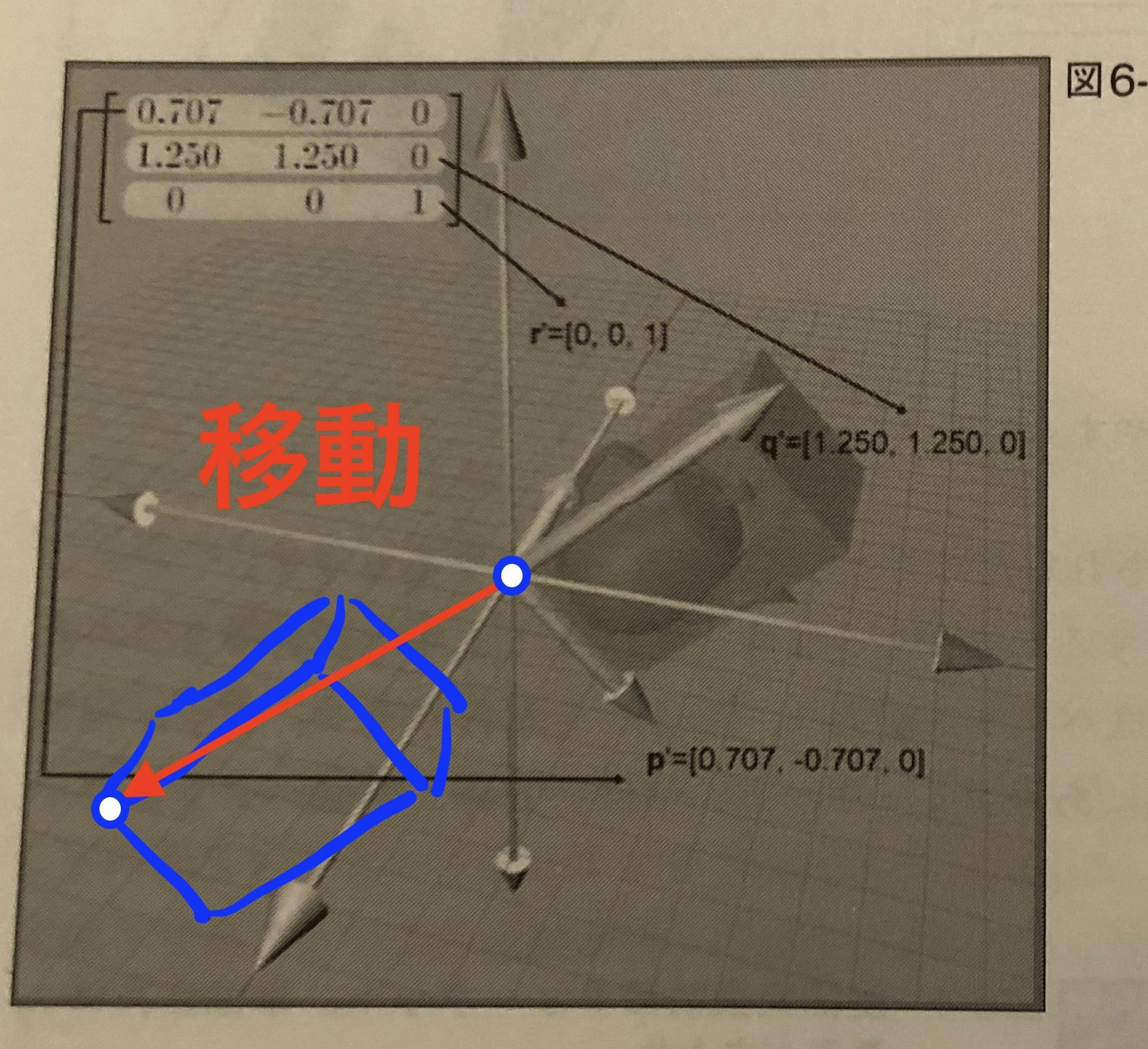
移動
ここまででお気づきになられた方もいるかもしれませんが、拡大縮小と回転は、原点を移動しません。
つまり、例のポッドの位置は変換前後で変わっていません。ここで、4*4行列の一番右の列が登場します。

青く囲まれている平行移動の部分です。ここの要素が、移動の役割をします。
以下のようにΔで示された移動量がそのままx, y, zそれぞれにプラスされるのです。

幾何学的に考えると、以下のようなイメージ。
大きさや向きは変えずに、原点だけを平行に移動しています。
投影
こちらの行列計算については複雑なので省略しますが、以下の行列の図の赤い部分の値の変更で表現できます。

まとめ
最後にもう一度、4*4行列を見てみましょう。

この4*4行列の何が便利かというと、回転と拡大縮小と(投影)と移動が1つで表現できることです。この行列の中に、オブジェクトに与えたい座標変換の全てを詰め込むことができます。
また、これは掛け算して合成することもできるため、OからA、AからB、BからCと3つの座標変換があったとしても掛け算すれば0からCの変換行列を作ることができるのです。
また別記事で、行列の掛け算や、実際にARKitやARCoreでどのAPIの組み合わせをすればいいのか紹介したいなと思います。