本記事は フューチャー Advent Calendar 2023 18日目の記事です。
昨日は、@RuyPKG さんの「asdf で開発言語と利用ツールのバージョン管理」でした。
はじめに
近年ChatGPTやStable Diffusionなど、生成AIが脚光を浴びています。これらはディープラーニングという機械学習アルゴリズムが用いられており、その計算のためにGPUが広く使われています。本記事ではGPUがディープラーニングで用いられる理由を解説します。
ディープラーニングでGPUが重宝される理由を理解するにはGPUの仕組みとディープラニングのアルゴリズムを簡単に理解する必要があるため、順に説明します。
GPUとは
GPUとは並列計算を得意とするプロセッサで。映像出力を主な役割としてPCに取り付けられることが多いです。通常はグラフィックボードという基盤の上に取り付けられています。グラフィックボードの主要なパーツはGPUの他にメモリと映像出力端子とPCI Express端子があります。
写真はWikipediaより引用:https://ja.wikipedia.org/wiki/%E3%83%93%E3%83%87%E3%82%AA%E3%82%AB%E3%83%BC%E3%83%89
グラフィックボード上のメモリはCPUと通信するメモリ(RAM)とは別物であり、VRAM(Video Random Access Memory)と呼ばれています。
映像出力端子はGPUで計算された結果を画面上に出力する端子で、規格としてはDisplay PortやHDMIが主流です。
PCI Express端子はマザーボードとグラフィックボードを物理的に接続し、通信する部分になります。グラフィックボードへの電源供給も担います。ちなみに昨今のGPUは電力消費が激しくPCI Expressからの電源供給だけでは足りないため、補助電源の端子も搭載されています。
電子計算機を構成するために必要なものは、プロセッサとメモリと電源と言われています。グラフィックボードにはそれら全てが揃っているいるため、これ単体で一つの電子計算機とみなすことができます。
GPUの仕組み
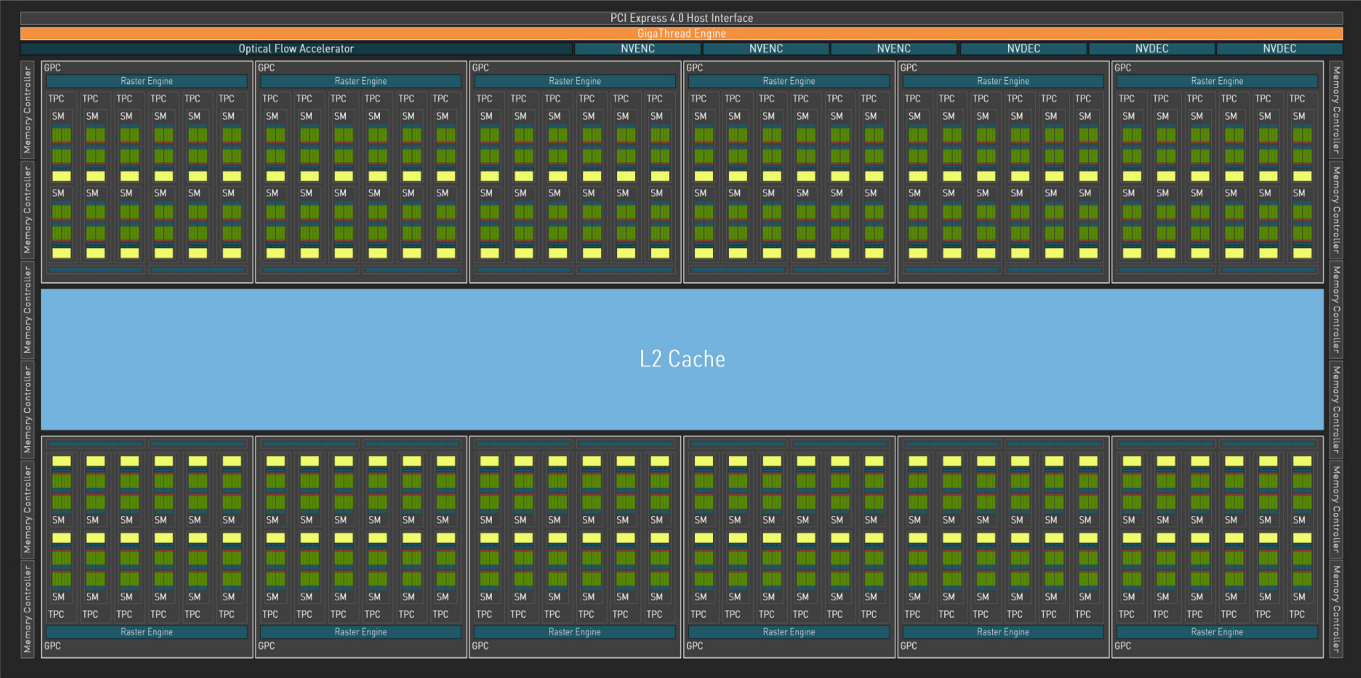
今回解説するGPUアーキテクチャは「Ada AD102」です。NVIDIAが公開しているペーパーで詳しく解説されています。2023年時点で最新のアーキテクチャであり、「NVIDIA RTX 40 Series」という製品群で出回っています。
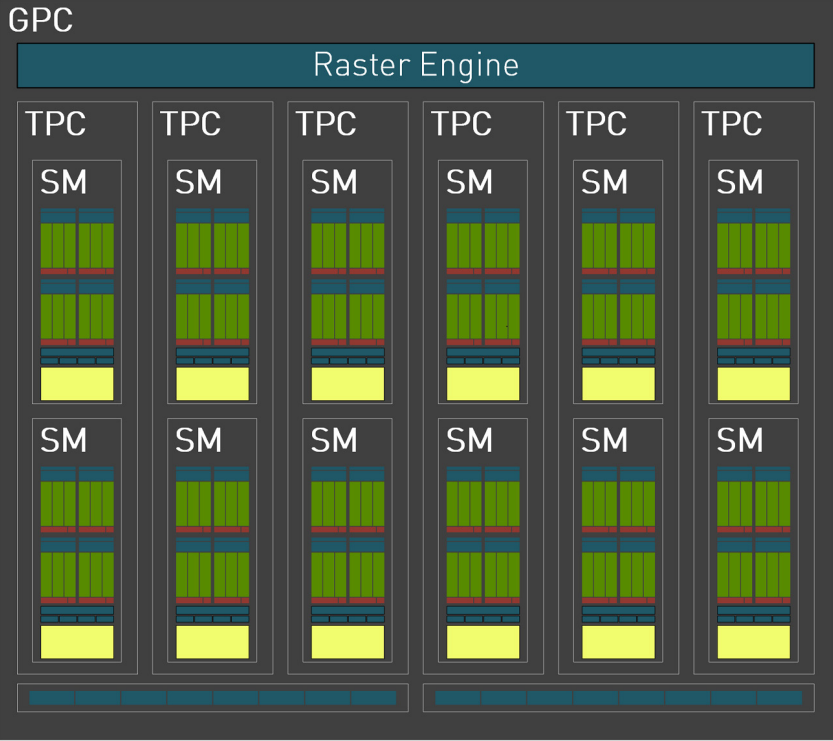
Graphics Processing Clusters (GPC)というクラスタが12個存在します。そして1つのGPCを拡大すると、以下のようになります。
Texture Processing Clusters (TPC)が6個、Streaming Multiprocessors (SM)が12個、CUDA Coreが128個存在します。CUDA CoreがCPUにおけるALUの部分に相当し、レジスタなどと通信しながら演算処理を行います。
重要なポイントはSMになります。1つのSM内部のCUDA Coreはそれぞれ異なるデータを保持できますが、与えられる命令は全て同じであり、同時に実行されます。従って、全てのGPCを合わせるとCUDA Coreは18432個あるため、これだけの数の並列演算が可能ということになります。
CPUは1つのデータに対して多数の命令を適用することを効率的に行う一方で、GPUは多数のデータに対して1つの命令を適用することを効率的に行います。このような計算理念の違いがCPUとGPUの本質的な違いと言えます。
これを著実に表現したNVIDIAによるデモンストレーションがありますのでぜひご覧ください。
GPUの得意な計算
GPUはその仕組み上、多数のデータに対して1つの命令を適用することを効率的に行えます。このような特性が活きる計算に行列演算があります。
例えば以下の単純な行列計算を見てみます。右辺の各要素の計算式に存在する演算子は全て同じであり、かつ他の要素の計算結果に依存することはないため、各要素は並列計算によって同時に計算可能ということになります。
\begin{bmatrix}
x_{11} & x_{12} \\
x_{21} & x_{22} \\
\end{bmatrix}
\begin{bmatrix}
y_{11} & y_{12} \\
y_{21} & y_{22} \\
\end{bmatrix}
=
\begin{bmatrix}
x_{11} \cdot y_{11} + x_{12} \cdot y_{21} & x_{11} \cdot y_{12} + x_{12} \cdot y_{22} \\
x_{21} \cdot y_{11} + x_{22} \cdot y_{21} & x_{21} \cdot y_{12} + x_{22} \cdot y_{22} \\
\end{bmatrix}
レイトレーシングやユークリッド変換など、画像情報処理では行列演算を多用します。このような背景からゲームや3Dモデリングの分野ではGPUが重宝されることになります。
ディープラーニングでの活用
ディープラーニングの全結合層では以下のように、特徴量ベクトル$\boldsymbol{X}$に対して重み行列$\boldsymbol{W}$をかける計算が大量に行われます。
\boldsymbol{y} = \boldsymbol{W}\boldsymbol{X}
例えばベクトル空間が$\mathbb{R}^{512 \times 3136}$の場合は以下のような計算になります。
\begin{bmatrix}
w_{1,1} & \cdots & w_{1,3136} \\
\vdots & \ddots & \vdots \\
w_{512,1} & \cdots & w_{512,3136}
\end{bmatrix}
\begin{bmatrix}
x_1 \\
\vdots \\
x_{3136}
\end{bmatrix}
=
\begin{bmatrix}
y_1 \\
\vdots \\
y_{512}
\end{bmatrix}
ディープラーニングでは特徴量ベクトルや重みの次元が膨大であることが一般的です。従って行列演算が得意なGPUを用いるメリットは非常に大きいと言えます。
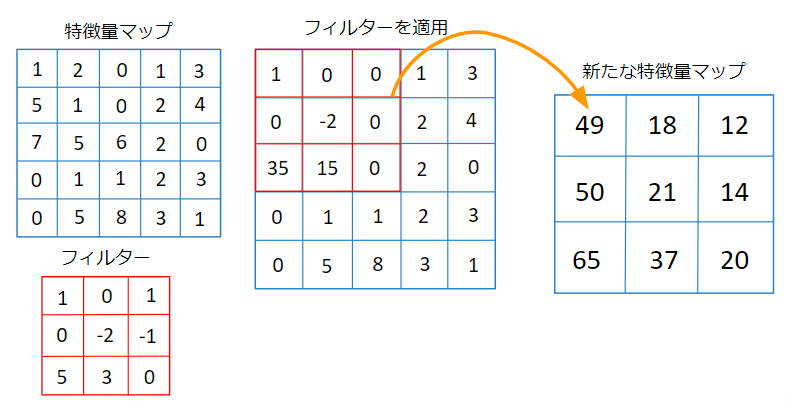
また、畳み込みニューラルネットワークでは以下のようにフィルターを特徴量マップに適用し、内積を計算していくことで新たな特徴量マップを生成します。
フィルターはスライディングウィンドウで特徴量マップを網羅するように適用されます。この時、各フィルターの適用は他の位置でフィルターを適用した計算結果に依存しません。従って、全てのフィルターの位置の計算を並列に計算可能ということになります。
このように、畳み込みニューラルネットワークはアルゴリズム自体が並列計算に向いており、GPUによる恩恵が非常に大きいということになります。
おわりに
今回はGPUの仕組みとディープラーニングのアルゴリズムを簡単に整理し、GPUがディープラーニングで用いられる理由を解説しました。昨今のAIは性能の向上に伴ってモデルの肥大化が顕著なので、現実的にはディープラーニングにはGPUが必須ですね。
今後の記事も見どころ満載です。ぜひご覧ください!