はじめに
この記事はフューチャー Advent Calendar 2022の13日目の記事です。
今回はRandom Network Distillation (RND)という深層強化学習手法についてご紹介したいと思います。
RNDは特に強化学習の原理的な部分である探索に焦点を当てた手法であり、個人的には深層強化学習分野の中でもかなり重要なアルゴリズムだと思っています。
強化学習や機械学習に興味のある方の参考になれば幸いです。
RNDの概要
RNDは2018年にOpenAIから発表された深層強化学習手法になります。エージェントに好奇心に相当するものを実装することで、環境の探索を促進します。これによりRNDでは今まで解くことのできなかった問題が解けるようになったということで大きな革新性があり、話題になりました。
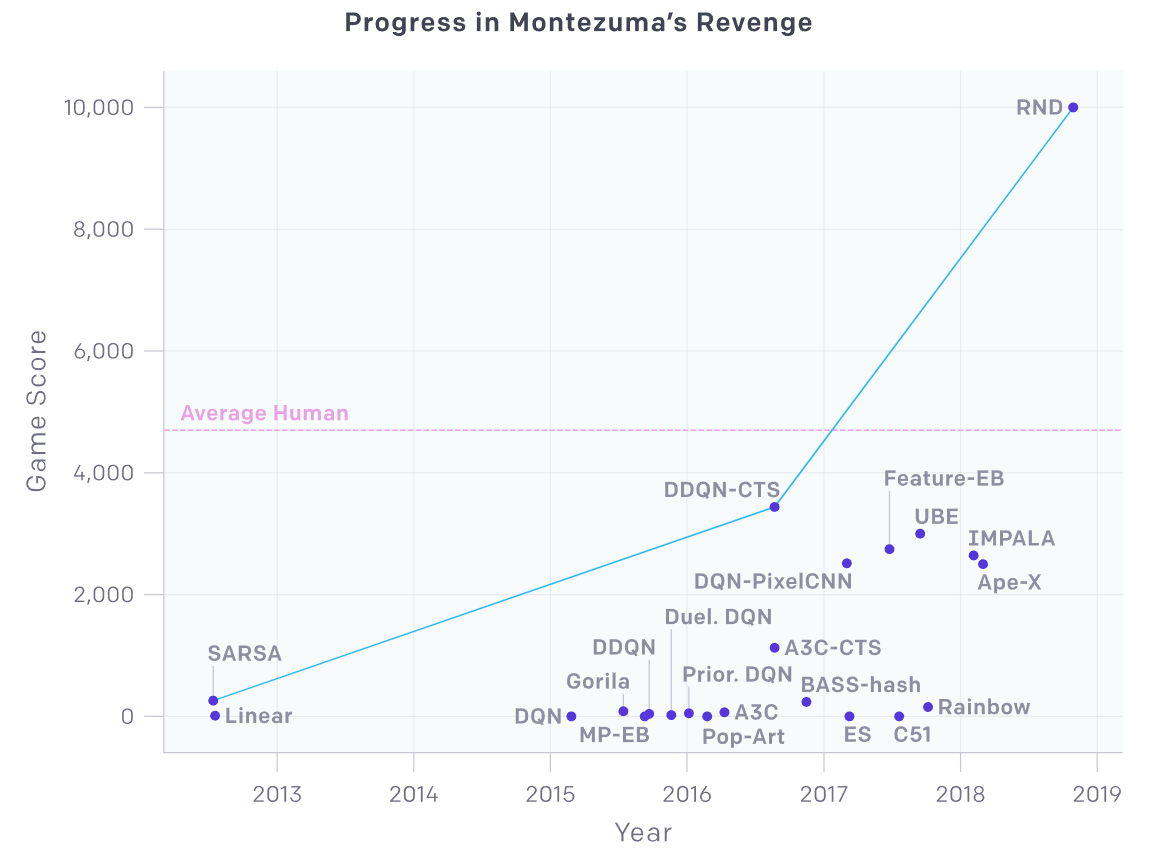
特に深層強化学習の分野でよくベンチマークとして用いられるAtari2600のゲームの内、Montezuma's Revengeという環境は報酬が非常に疎であり、AIでは攻略が困難であることが知られていました。RNDはこの環境でSOTA(State-of-the-Art)を達成し、報酬が疎な環境に対する代表的な解法となりました。
また、後続の手法であるNGU、そしてAgent57にも採用されています。
事前知識
この章ではRNDを理解する上で重要な知識を解説します。
報酬が疎な環境における問題点、好奇心探索について例題を用いて説明します。
強化学習における探索の問題点と解決策
強化学習は環境から得られた報酬によって学習を進めていきます。
Q学習における行動価値の更新式を見ても明らかですが、得られた報酬が次々と手前の状態に手繰り寄せられることで、次第に初期状態から価値の高い行動を選択できるようになっていきます。
$$
\begin{align}
Q(s,a) \leftarrow Q(s,a) + \alpha \lbrack r + \gamma \ max_{a^\prime} Q(s^\prime,a^\prime) - Q(s,a) \rbrack
\end{align}
$$
$s, a, r$はそれぞれ状態、行動、報酬を表します。$s^\prime, a^\prime$は次の状態、行動、$\alpha, \gamma$は内分比と割引率です。ポイントは学習するためには報酬が必要ということです。
では報酬が非常に疎であり、初期状態からかなり遠い状態で初めて報酬が得られるような環境ではどうなるでしょうか。ここでは簡単な例題を用いて考えてみたいと思います。
報酬が疎な環境の例
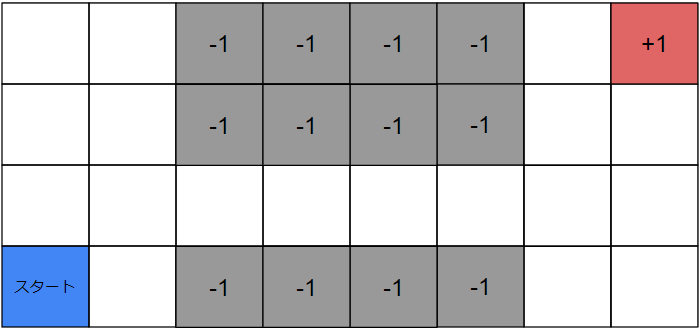
ここでは以下のような環境を例に考えてみたいと思います。
この環境は初期位置として左下の「スタート」の位置にエージェントが配置されます。
エージェントは上下左右移動の計4つの行動を選択することができます。
1ステップで1マス進むことができ、各マスに表示されている数字は報酬です。空白のマスは報酬0とします。
灰色のマスは崖になっており、踏んだ瞬間初期位置に戻されます。
右上のマスの報酬を獲得することを目的とします。
この環境での学習はどうなるか
強化学習は学習の初期段階ではランダムに行動することで探索を行い、報酬を探すことが一般的です。
しかしこの環境でランダム行動で報酬を獲得するためには、少なくとも途中の崖のエリアで4回連続「右」を選択することが必須になります。ということは行動は計4つであるため、崖のエリアだけで考えても右側のエリアに到達できる確率は$0.25^4$となり、報酬獲得可能性が極めて小さいことが分かります。
このように、報酬が疎であったり、報酬までの道のりが困難な場合はいつまでたっても報酬が得られず、学習が進まないという問題が存在します。
エージェントに好奇心を実装することで解決する
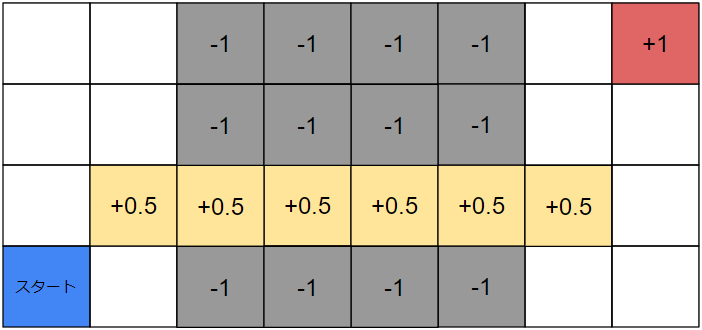
この環境では報酬が疎であることが問題で学習が進まないことが分かりました。逆に言うと、報酬がもう少しいい感じに存在すれば右上のマスまでたどり着けそうです。具体的には以下のような感じです。
このように報酬が配置されていれば、エージェントは$+0.5$の報酬をかき集めるように右側のエリアへ行き、やがて右上のマスに到達できそうです。
しかしこれは人間が環境の全貌を把握し、適切に報酬を設定できることが前提となります。もっと複雑な環境やそれこそゲームのような多次元環境ではこのように報酬を設定することは不可能です。また、そもそも最適解を求めるためのAIに人間の価値観はなるべく影響させたくありません。
ではどうするのかというと、エージェント自身にこのような中間報酬(サブゴールとも呼ばれます)に相当するものを生成してもらいます。
中間報酬を生成する研究はいくつかありますが、RNDはその中でも好奇心探索と呼ばれるものを用います。
好奇心探索
好奇心探索ではエージェントが目新しい状態に到達した場合に報酬を発生させます。逆に目新しくなくなっていくほど発生する報酬を小さくします。こうすることで、エージェントは目新しい状態を求めて探索を行うようになります。
このようにエージェント自らが生成する報酬を内部報酬と言います。
一方通常の環境から得られる報酬はこれと区別するため、外部報酬と呼ばれます。
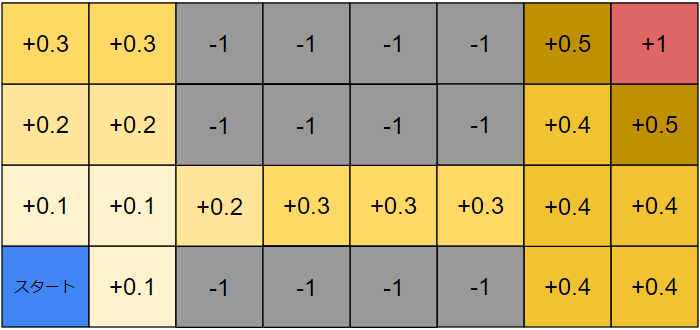
例えば少しだけ好奇心探索を行った後の潜在的な内部報酬をマッピングするとこのようになります。
初期位置周辺は最もエージェントが到達しやすい状態なので、内部報酬はあまり生成されなくなります。これは人間でいうところの「飽きた」に相当します。逆に初期位置から遠いほど内部報酬が存在します。エージェントは学習によってどの方向に移動すれば内部報酬が大きかったかを知っているため、その知識に従って未知の状態がありそうな方へ移動していきます。
難関である途中の崖エリアですが、これも崖に何度も落ちることでその状態が飽きてきます。すると自然に崖に落ちない方向に移動するようになります。また、来た道を戻ることもできますが、それよりも右に進む方が未知のエリアとなり、大きな内部報酬が得られるため、次第に右に行く動機の方が強くなります。
このように 「目新しい状態ほど大きな内部報酬を発生させる」 というメカニズムによって、探索を大きく促進します。
Noisy TV Problem
探索を大きく促進できる好奇心探索ですが、大きな問題が存在します。それがNoisy TV Problemと呼ばれるものです。
従来の手法では好奇心探索を実現するために、以下のような枠組みを用いていました。
$$
\begin{align}
\textbf{y} &= f(\textbf{X}) \\
r^i &= || \ \textbf{t} - \textbf{y} \ ||^2
\end{align}
$$
何らかの入力$\textbf{X}$からDeep Neural Network (DNN)などの関数$f$を用いて何らかの推定値$\textbf{y}$を出力します。
そして$\textbf{y}$とその教師データ$t$の誤差を用いて内部報酬$r^i$を計算します。
※ $r^i$は$r$の$i$乗ではなく、外部報酬と区別するために$intrinsic$の$i$を表示しています。
では何から何を推定するかですが、従来手法では現在の状態$s$から次の状態$s^\prime$を推定します。
つまり、内部報酬の生成は以下の計算式で行われます。
$$
r^i = || \ s^\prime - f(s) \ ||^2
$$
しかしこれには問題があります。それはある入力$s$に対する教師データ$s^\prime$が一意に定まらないことです。
強化学習が前提としているマルコフ決定過程では、状態遷移確率$P(s^\prime | s,a)$が存在します。これにより、次の状態は確率的に決まるということが大前提となっています。したがって単純な犬猫分類問題とは大きく異なり、教師データが朝令暮改のような形になるため、次の状態の推定がいつまでたってもうまくいかず、内部報酬が全然減らないという状況に陥ります。
これは例えると以下のような状況になります。
環境のランダム性によっていつまでも飽きない状況です。上記の例題でいうと、エージェントの初期位置周辺の内部報酬がいつまでも減少しないため、すぐ近くをうろうろしてるだけで報酬が得られ続けてしまい、遠くの方まで探索しに行く動機が薄れることになります。
RNDアルゴリズム
この章ではRNDのアルゴリズムについて、詳細に解説します。
内部報酬生成器
前章で見てきた通り、好奇心探索ではどのように内部報酬を生成するかが重要になります。RNDでは以下のように2つのDNNから内部報酬を生成します。
$$
\begin{align}
\textbf{t} &= f_1(\textbf{s}) \\
\textbf{y} &= f_2(\textbf{s}) \\
r^i &= || \ \textbf{t} - \textbf{y} \ ||^2 \\
Loss(\textbf{t},\textbf{y}) &= || \ \textbf{t} - \textbf{y} \ ||^2
\end{align}
$$
$f_1$はtarget network、$f_2$はpredictor networkと呼ばれています。
target networkは学習せず、predictor networkはtarget networkの出力を教師データとして学習します。target networkは学習しないため、ある入力に対する出力は終始同じになります。また、predictor networkの教師データは確率的ではなく、常に一意となるため、前章で解説したNoisy TV Problemを回避することができます。
さらにpredictor networkは学習するため、次第にtarget networkの出力に対する予測誤差が減少していきます。これにより頻繁に観測する状態の内部報酬は減少していくため、「目新しい状態ほど大きな内部報酬を発生させる」という好奇心探索で重要なメカニズムも実現できています。
方策
RNDでは方策勾配法の一種であるProximal Policy Optimization (PPO)を用いて方策を改善していきます。
PPOの目的関数は以下です。これを最大化するように学習していきます。
$$
L(\theta) = E \ \lbrack min(r_t (\theta )A_t, clip(r_t(\theta), 1 - \epsilon, 1 + \epsilon)A_t \rbrack
$$
$\theta$はモデルの学習パラメータ、$\epsilon$はクリップする範囲を決めるハイパーパラメータで、$t$はタイムステップです。
ここの$r_t(\theta)$は報酬ではなく、関数を表します。
$$
r_t(\theta) = \frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}
$$
RNDではアドバンテージの計算に工夫が存在します。以下のように、外部報酬と内部報酬のアドバンテージをそれぞれ計算してからそれらを足すことで最終的なアドバンテージとし、先の目的関数の計算に用います。
$$
\begin{align}
A_t^e &= r_t^e + \gamma \ r_{t+1}^e + \gamma^{T-t+1} \ r_{T-1}^e + \gamma^{T-t} \ V^e(s_T) - V^e(s_t) \\
A_t^i &= r_t^i + \gamma \ r_{t+1}^i + \gamma^{T-t+1} \ r_{T-1}^i + \gamma^{T-t} \ V^i(s_T) - V^i(s_t) \\
A_t &= A^e_t + A^i_t
\end{align}
$$
$r^e$、$r^i$はそれぞれ外部報酬、内部報酬を意味します。$V$は状態価値関数です。
このようにアドバンテージを分けて計算することで、外部報酬と内部報酬で独自の割引率を設定できるメリットがあります。
DNN構造
RNDの方策は2種類のアドバンテージを用いて更新されます。ということは状態価値の推定も2種類必要になります。したがってDNNの構造にも工夫が存在します。
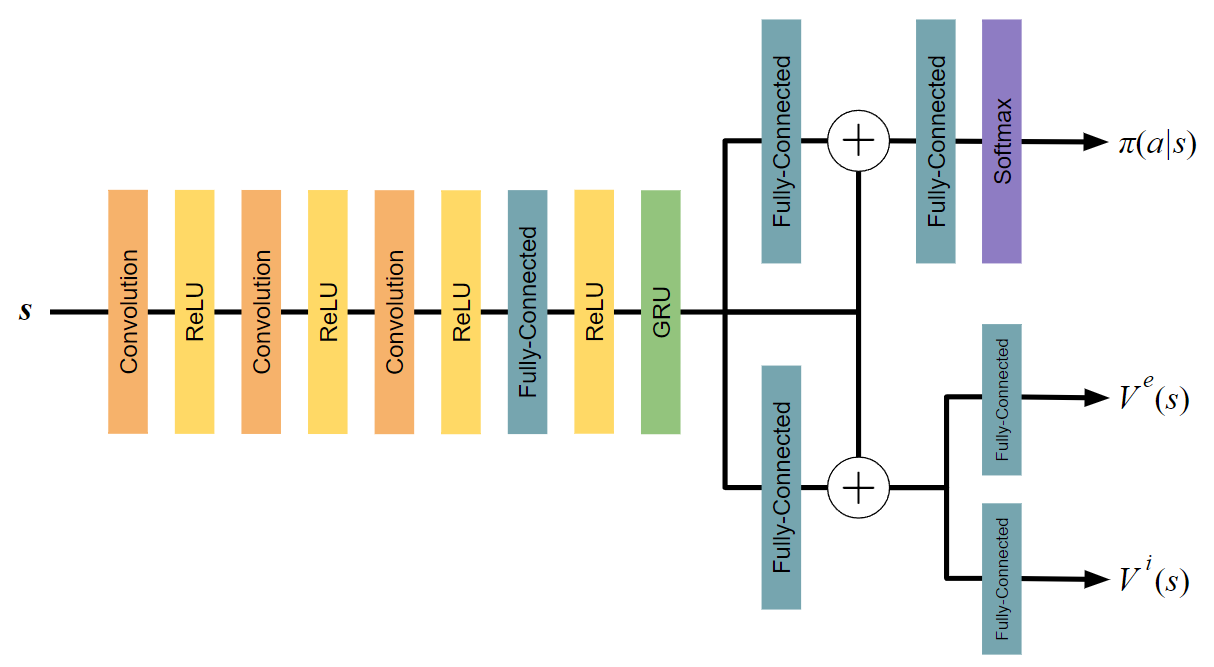
エージェントの方策に方策勾配法を用いた深層強化学習手法では、DeepMindが2016年に発表したA3CのDNN構造がよく用いられ、RNDはそれを以下のように拡張したものになっています。
図の$+$は要素ごとの加算を意味します。
状態$s$を入力することで、方策$\pi (a|s)$、外部報酬の状態価値$V^e(s)$、内部報酬の状態価値$V^i(s)$の3つが出力されます。また、Microsoft Researchより提案されたResidual Networkを採用することで勾配消失問題を軽減しています。さらに、GRUを用いることで時系列的特徴量を抽出することができます。これによって部分観測マルコフ決定過程の環境にも対応できるようになっています。
その他細かい工夫
RNDでは一般的な深層強化学習で使われる前処理などに加えて、追加で細かい工夫がなされています。
状態の標準化
DNNに入力する際に状態を標準化します。
しかし強化学習では状態$s$を含む学習データを環境とのインタラクションを通じて集めるため、初めからすべての状態が手に入っているわけではありません。よってはじめから真の状態データセットを用いて標準化することはできません。
そこで、状態を集めながら逐一その平均と分散を計算し、それらを一定の割合で更新していきます。
具体的な計算式は以下にわかりやすく掲載されています。
Wikipedia: https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Parallel_algorithm
逐一更新している状態の平均と分散を用いて以下の式で標準化を行います。
$$
x^\prime = \frac{x - mean(x)}{\sqrt{var(x)}}
$$
また、論文ではさらに外れ値を抑えるために標準化後の値を-5~5の間にクリッピングしています。
$$
x^{\prime \prime} = clip(x^\prime, -5, 5)
$$
内部報酬の割引報酬和
論文ではほとんど触れられていませんが、ソースコードを見ると内部報酬の割引報酬和の計算に工夫が見られます。
通常の強化学習では割引報酬和は未来方向に向かって割引率が累乗で適用され、合計値が計算されますが、この処理では過去方向に割引報酬和が計算されます。なぜこのような処理をするのかは正直理解しきれていません。
一応Github上ではこのようなやり取りがされています。
https://github.com/openai/large-scale-curiosity/issues/6
内部報酬の割引報酬和の正規化
上記で説明した内部報酬の割引報酬和に正規化を行います。
こちらも状態と同じように逐一分散を更新していきます。
そして以下の式で正規化を行います。
$$
x^\prime = \frac{x}{\sqrt{var(x)}}
$$
まとめ
今回は深層強化学習手法RNDを解説しました。
RNDは強化学習の原理的な探索という問題に焦点を当て、それを改善する手法であるということをご理解いただけたかと思います。
深層強化学習は2022年現在は社会実装の取り組みが増えてきたと感じます。今後のさらなる発展に注目していきたいです。
あと好奇心は知識の源泉ですね。一生大事にしていきたいと思いました!