はじめに
学習済みのニューラルネットワークのモデルを軽量化する手法として、蒸留、枝刈りなど様々なテクニックが存在します。
今回は、文献[1]を参考に、ニューラルネットワーク内の重み行列を行列積演算子と呼ばれるものに変換し、モデルを軽量化する手法について、PyTorchを用いて実装をしてみます。
本記事の内容について
文献[1]では、MNISTやCIFAR-10など、画像系のデータセットで実験を行っているのですが、本記事では少し趣向を変えて、テーブルデータセットでの実験を行ってみます。
今回はBank Marketing Data Set[2]を利用します。こちらは金融商品の電話営業のデータセットで、正例が1割程度の不均衡データになっております。
本記事では、行列積演算子への分解の話を中心とし、ニューラルネットワークやデータの前処理に関しての基礎的な説明は割愛します。
また、文献[1]の著者実装[3]では、TensorFlowを利用しているのですが、私が普段PyTorchを使うことが多いため、勉強も兼ねて、PyTorchで実装を行なっています。TensorFlow派の方は、実装については、著者実装[3]を直接見ていただくほうがわかりやすいかもしれません。
行列積状態(MPS)について
モチベーション
ニューラルネットワークの全結合層の重み行列は入力次元数$\times$出力次元数の行列です。扱うモデルにもよりますが、入力と出力の次元数は数千というオーダーのことも多く、非常に巨大な行列になります。
この巨大な行列を、複数の小さなテンソルの積に分解することで、パラメータ数を減らすことが目標になります。
特異値分解(SVD)
行列積状態の説明に入る前に、関連する重要な技術として、特異値分解について軽く触れます。
特異値分解は行列を分解する手法の一つで、$m \times n$行列$A$が与えられた時に、$ A=U \Sigma V^\dagger$となる分解を見つけます。このとき、行列$U$は$m \times m$のユニタリ行列、行列$V^\dagger$は$n \times n$のユニタリ行列です。$\Sigma$は非負の値を対角要素に持つ行列となり、この要素のことを特異値と呼びます。特異値は一意に定まり、一般に要素が大きい順に左上から順に並べた物を$\Sigma$とした分解を考えることが多いです。本記事もこれに倣います。
この分解だけでは、むしろ要素数は$ m \times m + n \times n + \min(m, n) $に増えてしまうので、嬉しいことはありません。
重要なのは、特異値の数は行列$A$のランクに等しいということです。低ランクの行列であれば、$\Sigma$の要素の大半は0になります。
ここで、行列$A$のランクを$r$とすると、特異値の数は$r$個なので、$\Sigma$は$r$行$r$列目の対角成分まで値があり、それよりも右、ならびに下の部分は0埋めされた行列となります。したがって、$U \Sigma V^{\dagger} $を計算するにあたって、$U$の$r+1$列目以降の成分、$V^{\dagger}$の$r+1$行目以降の成分は計算になんら影響を与えないことがわかります。
そのため、元行列$A$の情報を保持する目的では、$m \times r $の行列$\bar{U}$、$r \times n$の行列$\bar{{V}^\dagger}$と、$r$個の特異値を保持しておけば十分です。したがって、要素数は$(m+n+1)\times r$となり、$r \ll m,n$であれば、必要な情報量が減ります。
低ランク近似
先述の分解は近似を含まず、$A$を完全に再現することができます。ここでは、さらに特異値の中から$ k < r $個だけ値を取ることを考えます。
今、特異値は左上から順に大きなものが並んでいると考えているので、特異値が大きいものから順に$k$個残すことを考えます。このようにすることで、より小さな行列へと分解することができます。ただし、このケースでは小さな特異値を落としていることにより、誤差が生じるので、あくまで近似計算です。
行列積状態(MPS)への変換
ここまできたら、ついに本題の行列積状態への変換です。量子多体系の状態を記述するための手法の一つとして用いられることが多いですが、ここでは一般のテンソルを分解するための手法として活用します。
テンソルに対して、一つの軸を行に、他の軸をまとめて列とみなして、先ほどの特異値分解を繰り返し適用することで、複数のテンソルの積に分解します。
ここでは、あえて行列を多次元のテンソルとみなして、このテクニックを活用します。
あまり抽象的な話ばかりをしていてもイメージが湧かないと思うので、以下では具体例として、$256 \times 256$の行列を4つのテンソルの積に分解することを考えます。
まず、この行列を$16 \times 16 \times 16 \times 16$のテンソルとみなします。実装上はNumpyのreshapeに相当する操作です。この4つの軸でテンソルを分解します。
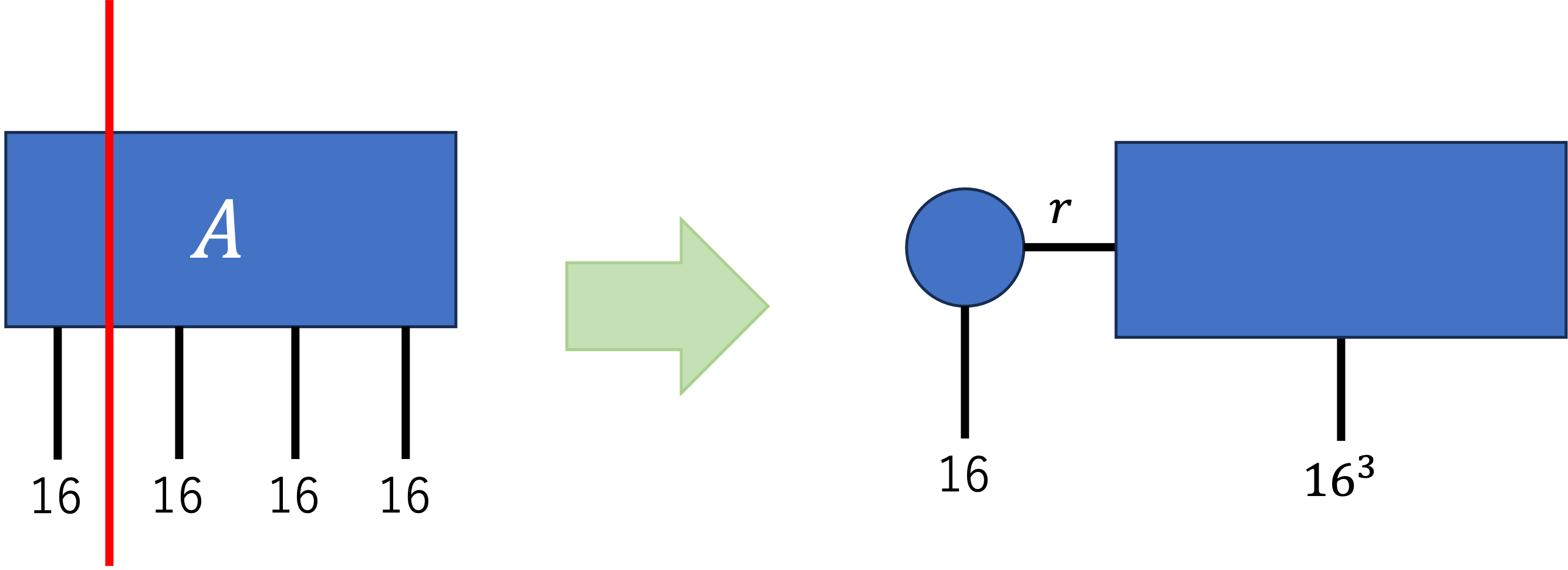
最初に、このテンソルを$16 \times 16^3$の行列とみなし、特異値分解をします。これにより、$16 \times r$と$r \times 16^3$の行列ができあがります。(ここでは、$U$と$\Sigma V^{\dagger} $で二つの行列としています。)
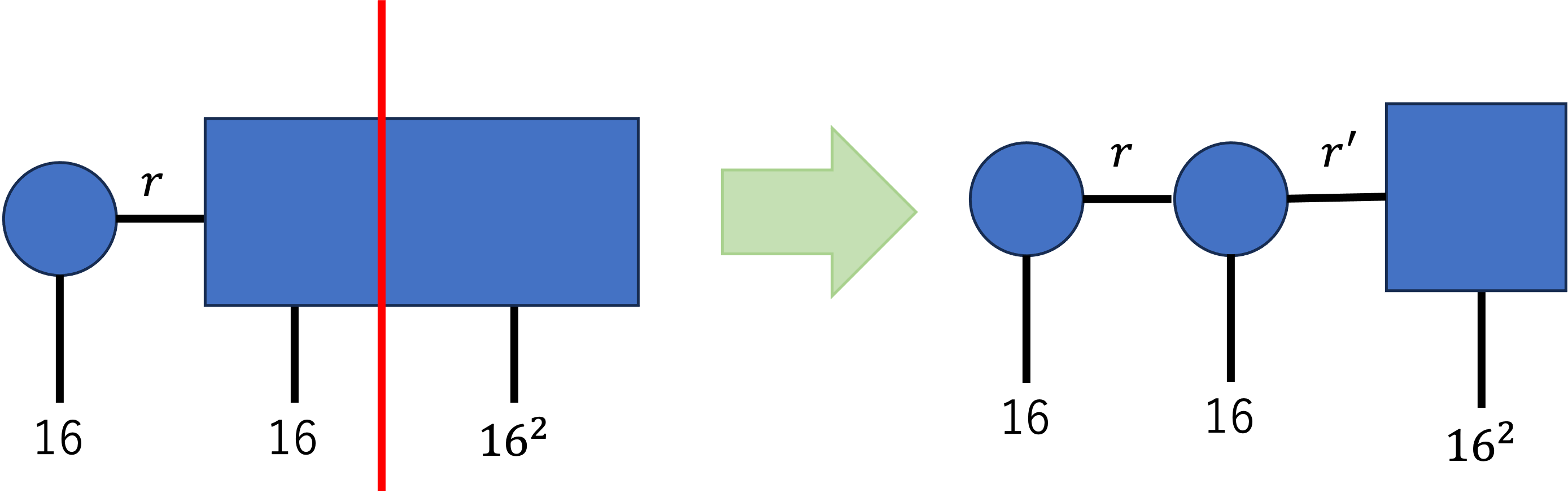
次に、出来上がった$r\times16^3$の行列を、$(r\times16)\times16^2$の行列とみなして、同じように特異値分解を行います。
ここで得られた$(r \times 16)\times r'$の行列は、$r\times16\times r'$の3次元のテンソルに変換します。
この操作を繰り返すことで、最終的には2次元のテンソル$\times$3次元のテンソル$\times$3次元のテンソル$\times$2次元のテンソルといった形の4つのテンソルの積に分解されます。
ここでは、状態の分解を示しましたが、同様に演算子としてのテンソルを分解することが可能です。入出力の軸を切り分けることで、行列積演算子(MPO)を作成することが可能です。これについては以下の実装例の中で実際に確認していきます。
実装
前置きが長くなりましたが、ここからは実装を行います。
今回使用したライブラリのバージョンは以下の通りです。
Python 3.7.6
numpy 1.19.5
pytorch 1.13.1
まず最初に、必要なライブラリをimportします。
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from tqdm.notebook import tqdm
from sklearn import metrics
前処理
今回扱うデータについては、事前に以下の処理を施しています。
- "duration"カラムの削除:モデルの用途をどう見るかですが、ターゲットとの相関が非常に高く、リークに近い特徴量なので、削除しておきます。
- カテゴリデータの変換:今回、ニューラルネットワークを用いるため、pandasのget_dummiesを使用して、事前にOne-Hot Encodingをしています。
- 数値データの正規化:0-1の範囲になるように正規化しています。
- データの分割:trainとtestに8:2で分割した後、さらにtrainをtrainとvalidに8:2で分割しています。(全体で64:16:20の比率)
不均衡データではありますが、特にアンダーサンプリング等は施していません。上記の処理を施すことで、ラベルを除くと、特徴量が62次元のデータになると思います。
ニューラルネットワークの学習
まずは、普通の全結合ニューラルネットワークで学習します。
今回は3層の全結合層を持つニューラルネットワークを用意します。今回のタスクは二値分類なので、最終出力は1次元にし、シグモイド関数を通しています。
もう少し小さいモデルでも性能はほとんど変わらないのですが、ある程度大きい行列を分解したいので、あえて少し大きくしています。
torch.manual_seed(0)
model = nn.Sequential(
nn.Linear(62, 256),
nn.ReLU(),
nn.Linear(256, 256),
nn.ReLU(),
nn.Linear(256, 1),
nn.Sigmoid()
)
ハイパーパラメータは特に最適化していませんが、以下で実験を行いました。
epochs = 200
batch_size = 128
lr = 1e-4
early_stopping_rounds = 20
optimizer = torch.optim.Adam(model.parameters(), lr)
criterion = nn.BCELoss()
学習については以下のコードで実行します。
best_valid_loss = 100
best_epoch = 0
best_params = None
early_stopping_count = 0
train_loss_records = []
valid_loss_records = []
for epoch in tqdm(range(1, epochs+1)):
sum_loss = 0
for X, y in train_loader:
optimizer.zero_grad()
output = model(X)
loss = criterion(output, y.reshape(-1,1))
sum_loss += loss
loss.backward()
optimizer.step()
train_loss_records.append(float(sum_loss) / len(train_loader))
# validation
with torch.no_grad():
output = model(valid_X)
valid_loss = criterion(output, valid_y.reshape(-1,1))
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
best_epoch = epoch
best_params = model.state_dict()
early_stopping_count = 0
else:
early_stopping_count += 1
valid_loss_records.append(float(valid_loss))
if early_stopping_count >= early_stopping_rounds:
print(f"early stopping at epoch {best_epoch}")
print(f"best valid loss: {best_valid_loss:.4f}")
break
if epoch % 10 == 0:
print(f"epoch: {epoch}")
print(f"valid loss: {valid_loss:.4f}")
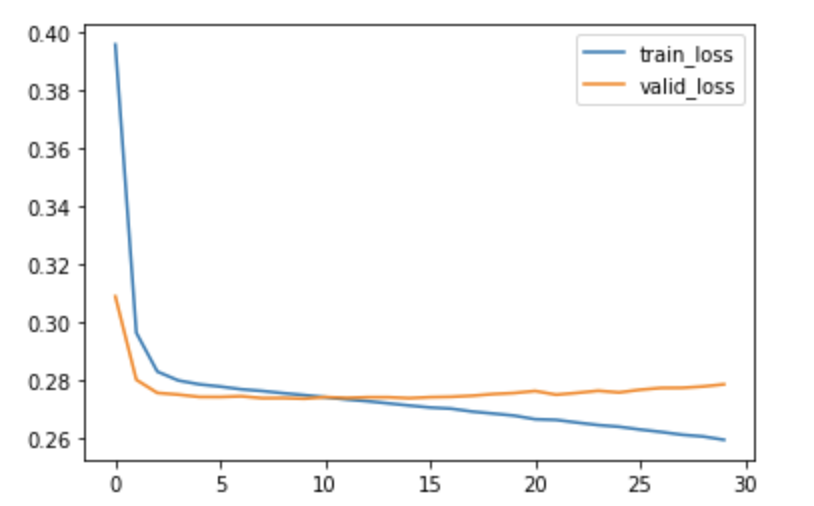
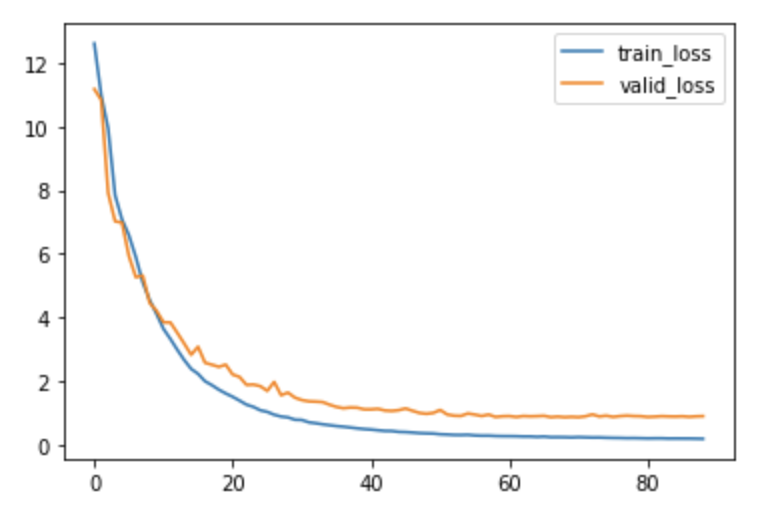
結果としては、10epoch目でバリデーションロスが最小となり、early stoppingしました。ロスの変化を確認すると以下の通りになっており、うまく学習できていそうです。
early stoppingのタイミングの重みを読み出し、テストデータでの性能を確認します。
model.load_state_dict(best_params)
with torch.no_grad():
output = model(test_X)
loss = criterion(output, test_y.reshape(-1, 1))
print(f"BCELoss: {float(loss):.4f}")
output_label = [1 if i >= 0.5 else 0 for i in output]
acc = metrics.accuracy_score(test_y, output_label)
recall = metrics.recall_score(test_y, output_label)
precision = metrics.precision_score(test_y, output_label)
print("------")
print(f"accuracy: {acc:.4f}")
print(f"recall: {recall:.4f}")
print(f"precision: {precision:.4f}")
roc_auc = metrics.roc_auc_score(test_y, output.detach().numpy())
print(f"roc_auc: {roc_auc:.4f}")
BCELoss: 0.2766
------
accuracy: 0.8978
recall: 0.2285
precision: 0.6122
roc_auc: 0.7938
いくつかの指標を出力していますが、今回は不均衡データなので、ここから先は基本的にはroc_aucを見て、評価していこうと思います。
重み行列の分解
それでは、学習したモデルから重み行列を取り出し、行列積演算子に分解していきます。ここでは、一番大きい$256\times 256$の行列を分解します。
まずは取り出した重み行列を適当な変数に格納します。
W_h = model.state_dict()["2.weight"].detach().numpy()
これを、分解したい形に合わせて、軸が合うようにreshapeとtransposeをし、4次元のテンソルにします。
W_h_reshaped = W_h.reshape(4,4,4,4,4,4,4,4)
W_h_tensor = W_h_reshaped.transpose(0,4,1,5,2,6,3,7).reshape(16,16,16,16)
軸を合わせる、というのは以下の図のように、分解後のテンソルネットワークにおいて、入力と出力の関係が合うようにするための操作です。

このテンソルに対し、特異値分解を繰り返し適用しながら、分解を行います。
from numpy.linalg import svd
u1, s1, vh1 = svd(W_h_tensor.reshape(16,16**3),full_matrices=False)
M1 = u1
u2, s2, vh2 = svd((np.diag(s1) @ vh1).reshape(16**2, 16**2),full_matrices=False)
M2 = u2.reshape(16,16,16**2)
u3, s3, vh3 = svd((np.diag(s2) @ vh2).reshape(16**3, 16),full_matrices=False)
M3 = u3.reshape(16**2,16,16)
M4 = np.diag(s3) @ vh3
ここでは、低ランク近似はおこなっていません。また、一旦入力と出力をまとめて一つの軸としています。まずは、これを掛け合わせて元の行列に戻ることを確認します。
def reconstruct_matrix(M1,M2,M3,M4):
matrix = np.einsum("ij,jlm,mno,op -> ilnp",M1,M2,M3,M4,optimize=True).reshape(4,4,4,4,4,4,4,4).transpose(0,2,4,6,1,3,5,7).reshape(256,256)
return matrix
W_h_reconstructed = reconstruct_matrix(M1,M2,M3,M4)
## 誤差のノルムの大きさを確認
print(np.linalg.norm(W_h - W_h_reconstructed)/np.linalg.norm(W_h))
# 3.737868e-07
## ベクトルとみなしてコサイン類似度を確認
def cos_sim(v1, v2):
return np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))
print(cos_sim(W_h.reshape(-1), W_h_ap.reshape(-1)))
# 1.0
多少の数値誤差はありますが、ほとんど元の行列を再現できています。
それでは、次に低ランク近似を行います。
chi_max = 32 # 最大のボンド次元 (=残す特異値の数)
## M1 と M2をつなぐボンド
chi_12 = min(chi_max,M1.shape[1])
## M2 と M3をつなぐボンド
chi_23 = min(chi_max,M2.shape[2])
## M3 と M4をつなぐボンド
chi_34 = min(chi_max,M3.shape[2])
M1_ap = M1[:,:chi_12]
M2_ap = M2[:chi_12,:,:chi_23]
M3_ap = M3[:chi_23,:,:chi_34]
M4_ap = M4[:chi_34,:]
W_h_ap = reconstruct_matrix(M1_ap,M2_ap,M3_ap,M4_ap)
## 誤差のノルムの大きさを確認
print(np.linalg.norm(W_h - W_h_ap)/np.linalg.norm(W_h))
# 0.7576054
## ベクトルとみなしてコサイン類似度を確認
print(cos_sim(W_h.reshape(-1), W_h_ap.reshape(-1)))
# 0.64725477
こちらはそれなりに誤差が出ています。これに関してはパラメータ数と精度のトレードオフとなり、ボンド次元を変更することで調整できます。
今回のケースでは、誤差こそ大きいですが、$256\times 256 = 65,536$個あった要素数が$16,896$個に抑えられています。
ニューラルネットワークへの導入
分解されたテンソルを重み行列として持ち、出力を計算するようなニューラルネットワークのレイヤーを定義します。
今回は、この$256 \times 256$の分解のことだけを考えたクラスをつくります。汎用的なクラスを作ると、分割の数や、各軸の次元数など、選択肢の自由度が高く、実装が面倒なので、今回は4つのテンソルに分割し、すべての軸の次元数は等しいものとします。
また、先ほどはNumpyを使って実装していたのですが、自動微分を利用したいため、以下ではtorchの関数で実装しています。
class MPO_layer(nn.Module):
def __init__(self, input_dim, output_dim, bond_dim):
super().__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.bond_dim = bond_dim
# 今回は同じサイズに4分割する前提
assert int(input_dim ** (1/4)) ** 4 == input_dim
assert int(output_dim ** (1/4)) ** 4 == output_dim
tensor_input_dim = int(input_dim ** (1/4))
tensor_output_dim = int(output_dim ** (1/4))
# 重みを格納する行列の定義
chi_12 = min(tensor_input_dim*tensor_output_dim, bond_dim)
weight_1 = torch.randn(size=(tensor_output_dim, tensor_input_dim, chi_12))
self.weight_1 = nn.Parameter(weight_1)
chi_23 = min((tensor_input_dim*tensor_output_dim)**2, bond_dim)
weight_2 = torch.randn(size=(chi_12, tensor_output_dim, tensor_input_dim, chi_23))
self.weight_2 = nn.Parameter(weight_2)
chi_34 = min((tensor_input_dim*tensor_output_dim), bond_dim)
weight_3 = torch.randn(size=(chi_23, tensor_output_dim, tensor_input_dim, chi_34))
self.weight_3 = nn.Parameter(weight_3)
weight_4 = torch.randn(size=(chi_34, tensor_output_dim, tensor_input_dim))
self.weight_4 = nn.Parameter(weight_4)
# バイアスを格納するベクトルの定義
bias = torch.empty(output_dim).uniform_(-1, 1)
self.bias = nn.Parameter(bias)
def forward(self, x):
x_tensor = x.reshape(-1, 4, 4, 4, 4)
output = torch.einsum("ijl,lmno,opqr,rst,ujnqt -> uimps", self.weight_1, self.weight_2, self.weight_3, self.weight_4, x_tensor).reshape(-1, 256)
output += self.bias
return output
このクラスを使ったニューラルネットワークを新たに定義します。
torch.manual_seed(0)
model_2 = nn.Sequential(
nn.Linear(62, 256),
nn.ReLU(),
MPO_layer(256, 256, 32),
nn.ReLU(),
nn.Linear(256, 1),
nn.Sigmoid()
)
state_dictに直接、先ほど分解を試した結果を代入して、性能を確認してみます。それ以外のレイヤーは前回のモデルのウェイトをそのまま代入します。
上で定義したレイヤーでは、入出力の軸を分けたテンソルネットワークを想定しているので、分解の結果をreshapeして代入します。
model_2[0].weight = nn.Parameter(model.state_dict()["0.weight"])
model_2[0].bias = nn.Parameter(model.state_dict()["0.bias"])
model_2[2].weight_1 = nn.Parameter(torch.from_numpy(M1_ap.reshape(4, 4, chi_12)))
model_2[2].weight_2 = nn.Parameter(torch.from_numpy(M2_ap.reshape(chi_12, 4, 4, chi_23)))
model_2[2].weight_3 = nn.Parameter(torch.from_numpy(M3_ap.reshape(chi_23, 4, 4, chi_34)))
model_2[2].weight_4 = nn.Parameter(torch.from_numpy(M4_ap.reshape(chi_34, 4, 4)))
model_2[2].bias = nn.Parameter(model.state_dict()["2.bias"])
model_2[4].weight = nn.Parameter(model.state_dict()["4.weight"])
model_2[4].bias = nn.Parameter(model.state_dict()["4.bias"])
こちらでテストデータでの性能を確認してみます。
with torch.no_grad():
output = model_2(test_X)
loss = criterion(output, test_y.reshape(-1, 1))
print(f"BCELoss: {float(loss):.4f}")
output_label = [1 if i >= 0.5 else 0 for i in output]
acc = metrics.accuracy_score(test_y, output_label)
recall = metrics.recall_score(test_y, output_label)
precision = metrics.precision_score(test_y, output_label)
print("------")
print(f"accuracy: {acc:.4f}")
print(f"recall:{recall:.4f}")
print(f"precision:{precision:.4f}")
roc_auc = metrics.roc_auc_score(test_y, output.detach().numpy())
print(f"roc_auc:{roc_auc:.4f}")
BCELoss: 0.3369
------
accuracy: 0.8974
recall:0.2394
precision:0.6011
roc_auc:0.7865
先ほどより若干の性能の低下が見て取れますが、問題なく予測はできていそうです。再構成後の行列の誤差の割には性能がキープできている印象です。後ろの層でうまくカバーできているのでしょうか。
追加学習
枝刈りの際にも、枝刈り後のネットワークで追加の学習をすることがあるように、行列積分解したネットワークでの追加学習を実施してみます。
勾配計算はPyTorchの自動微分の機能でうまいことやってくれます。
epochs = 200
lr = 1e-5
optimizer_2 = torch.optim.Adam(model_2.parameters(), lr)
criterion = nn.BCELoss()
best_valid_loss = 100
best_params = []
best_epoch = 0
early_stopping_count = 0
train_loss_records = []
valid_loss_records = []
for epoch in tqdm(range(1, epochs+1)):
sum_loss = 0
for X, y in train_loader:
optimizer_2.zero_grad()
output = model_2(X)
loss = criterion(output, y.reshape(-1,1))
sum_loss += loss
loss.backward()
optimizer_2.step()
train_loss_records.append(float(sum_loss) / len(train_loader))
# validation
with torch.no_grad():
output = model_2(valid_X)
valid_loss = criterion(output, valid_y.reshape(-1,1))
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
best_epoch = epoch
best_params = model_2.state_dict()
early_stopping_count = 0
else:
early_stopping_count += 1
valid_loss_records.append(float(valid_loss))
if early_stopping_count >= early_stopping_rounds:
print(f"early stopping at epoch {best_epoch}")
print(f"best valid loss: {best_valid_loss:.4f}")
break
if epoch % 10 == 0:
print(f"epoch: {epoch}")
print(f"valid loss: {valid_loss:.4f}")
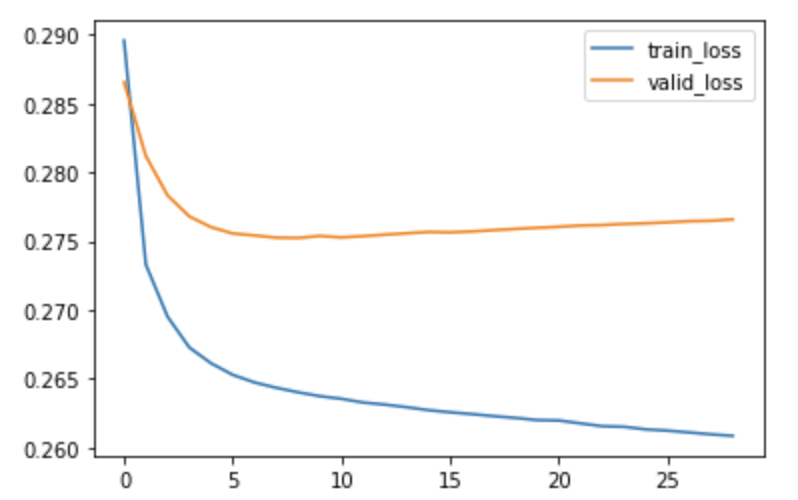
今回は9epoch目がベストな結果となり、early stoppingしました。学習中のロスの変動のグラフが以下になります。
元のモデルが学習済みなこともあり、やや過学習気味の挙動に見えますが、ひとまずこちらでテストデータでの性能を確認してみますと、以下のようになりました。
BCELoss: 0.2750
------
accuracy: 0.8979
recall:0.2394
precision:0.6077
roc_auc:0.7967
概ね元のモデルの性能を取り戻しており、十分な性能が発揮できているように見えます。
レイヤーのパラメータ数も、先述の通り65,536から16,896に抑えられており、無事モデルの圧縮ができました。
(参考)分解後のモデルで0から学習
行列積状態に分解した後のモデルで追加学習ができるということは、最初からこの形のネットワークを定義して学習することも可能です。
ランダムな重みを初期値として与え、このモデルを学習するとどのようになるかを確認してみました。
BCELoss: 0.8619
------
accuracy: 0.8695
recall:0.2927
precision:0.3876
roc_auc:0.6732
まず、ロスの変化になりますが、ロスが下がるのが非常に遅いです。また、十分に小さな値まで下がりきりませんでした。私の環境では69 epoch目にearly stoppingし、この際のバリデーションデータでのロスが0.8686と、先ほどの結果と比べると非常に大きいです。
また、テストデータでの性能も同程度のロス関数の値となっており、roc_aucなどもあまりよくない結果になっております。
ロス自体はepochが進むにつれて下がっていっているので、学習自体はちゃんと進行していますが、元のモデルと同等の水準のロスには到達できませんでした。おそらく局所解にはまってしまっているのだと思います。
こちらの例は学習率を$10^{-4}$として実行した結果なのですが、これよりも大きな学習率では、すべてを正例と予測する、もしくはすべてを負例と予測するような極端なケースにハマりやすいように感じました。
関数の形として、あまり最適化がしやすい形にはなっていないのかもしれません。
まとめ
今回は、ニューラルネットワークの重み行列を行列積演算子へと分解することで、モデルのパラメータ削減を行える手法について、実装してみました。
パラメータ削減後のモデルも、PyTorchの自動微分を用いて学習可能なため、追加学習も可能です。
今回は小規模なモデルで、$256 \times 256$の全結合層一つのみを分解しましたが、複数の層に導入する、より大きな行列を分解する、などの実験をしてみるのも面白いかもしれません。
以上です。