はじめに
量子コンピュータの実用に向けての大きな課題として、エラーの問題があります。現在の量子コンピュータは各部品のエラー率が非常に高く、実用的な用途の規模の計算に耐えられません。
これを解決するためには、ハードウェアとソフトウェアの双方で様々な研究が進められていますが、ソフトウェア側での手法の一つとして誤り訂正符号の利用があります。誤り訂正符号では、元の情報をうまく冗長化することで、エラーが発生した場合にも、エラーを特定し、元の状態への復元を行うことを目指します。
量子コンピュータにおいては、各種ゲート計算によるエラーも大きいため、符号化された論理量子ビットの状態のまま、各種ゲート操作に相当する操作を行い、ゲート操作に伴うエラーを修正できることが望ましいです。このような操作のことを論理ビット操作と呼びます。
本記事では、誤り訂正符号の一種であるSteane符号を用い、符号化された論理量子ビットに対して、論理量子ビット操作を加えることで、ベル状態を作成してみます。
本記事の内容は、東京大学「量子ソフトウェア」寄付講座[1]内で実施された第4回量子ソフトウェアハンズオン(産学協働ゼミ)[2]の演習資料を元に作成しています。
Steane符号
まずは今回用いるSteane符号について、簡単に解説します。
Steane符号は7量子ビットで構成される誤り訂正符号です。1量子ビットまでのエラーを検知・訂正できる符号になっています。
理論的な説明については本記事では割愛しますが、CSS符号と呼ばれる符号のクラスに属するものの一つで、今回利用したい論理量子ビット操作の実装が比較的簡単なため、採用しました。
今回用いる実装では、符号化後の論理状態$ \lvert 0_L \rangle, \lvert 1_L \rangle$としては、以下のようになっています。
$$ \lvert 0_L \rangle = \frac{1}{\sqrt{8}}\bigl(\lvert 0000000 \rangle + \lvert 0011101 \rangle + \lvert 0101011 \rangle + \lvert 0110110 \rangle + \lvert 1000111 \rangle + \lvert 1011010 \rangle + \lvert 1101100 \rangle + \lvert 1110001 \rangle \bigr) $$
$$ \lvert 1_L \rangle = \frac{1}{\sqrt{8}}\bigl(\lvert 1111111 \rangle + \lvert 1100010 \rangle + \lvert 1010100 \rangle + \lvert 1001001 \rangle + \lvert 0111000 \rangle + \lvert 0100101 \rangle + \lvert 0010011 \rangle + \lvert 0001110 \rangle \bigr) $$
論理ビット操作
誤り訂正符号では、複数の物理量子ビットを用いて一つの論理量子ビットを作成します。作成された論理量子ビットに対する論理ビット操作の実装方法は符号によって異なります。
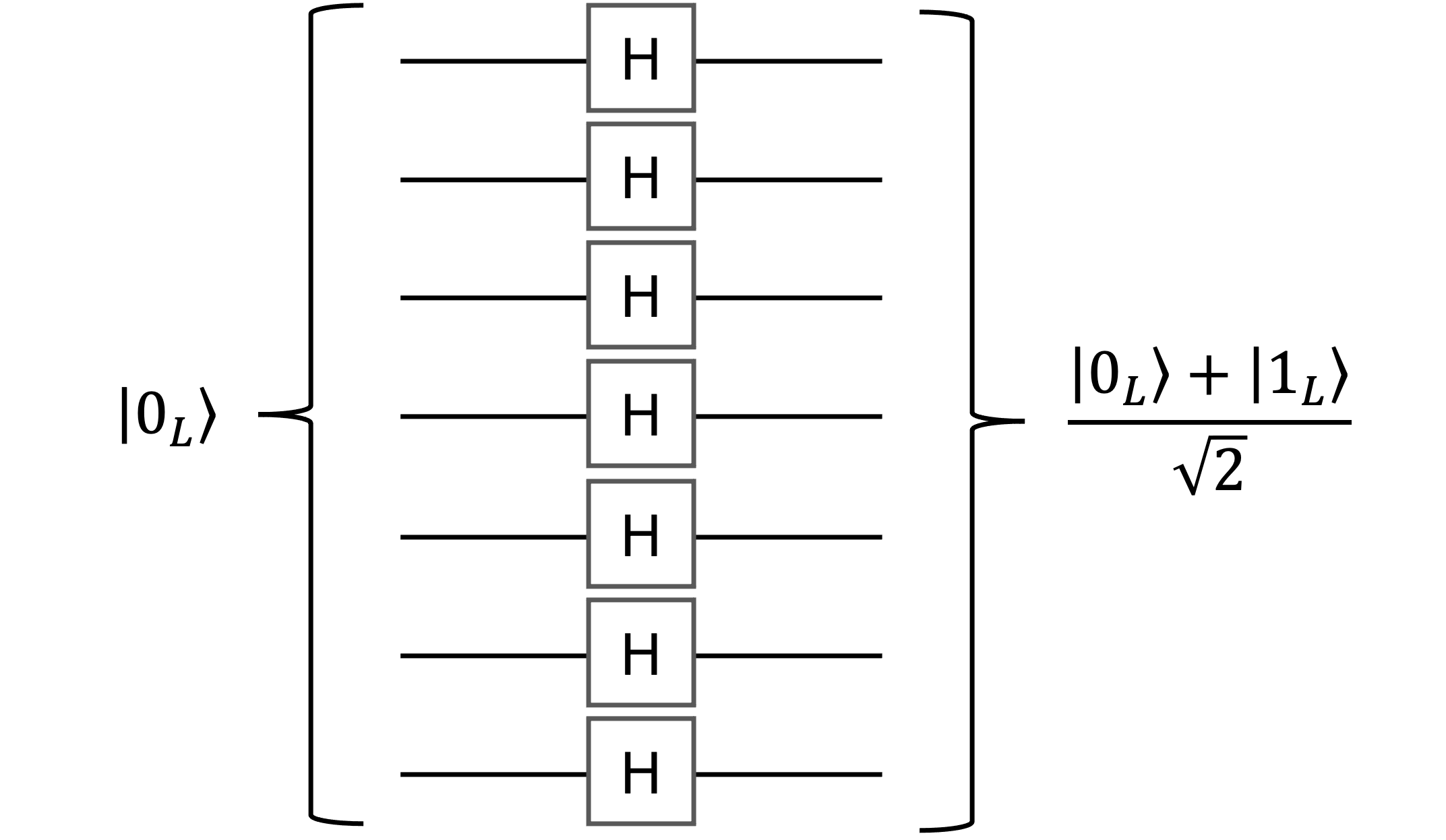
今回用いるSteane符号は、論理Hゲートや論理CNOTゲートの実装が非常に簡単です。例えば、論理Hゲートであれば、論理量子ビットを構成するすべての物理量子ビットに並列にHゲートをかけることで実現できます。論理CNOTゲートの場合も同様です。
このような性質を"Transversality"と呼びます。残念ながら、すべてのゲート操作に対して、このような単純な論理ビット操作の実装ができるわけではないです。本記事では詳細については触れませんが、例えばSteane符号においては、論理Tゲートはこのような簡単な実装はできず、もう少し工夫が必要になります。
実装
今回はQiskitのシミュレータを用いて実装を行います。
まずは必要なライブラリのインポートを行います。
from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator
from qiskit.tools.visualization import plot_histogram
from qiskit_aer.noise import pauli_error
また、いくつかのパラメータを定義しておきます。
n_shots = 1000 # シミュレーターでのサンプリング回数
backend_sim = AerSimulator() # シミュレーターの用意
p_error = 0.1 # エラー確率
エラーの定義
今回想定するエラーとしては、ビット反転と位相反転の2種が等確率で独立に発生するようなものを考えます。これを関数として用意しておきます。
def make_bitphase_error_channel(p_error, print_flag=True):
bit_flip = pauli_error([('X', p_error), ('I', 1 - p_error)])
phase_flip = pauli_error([('Z', p_error), ('I', 1 - p_error)])
bitphase_flip = bit_flip.compose(phase_flip)
if print_flag: # エラーの構成を可視化する
print(bitphase_flip)
return bitphase_flip
bitphase_flip = make_bitphase_error_channel(p_error)
まずは誤り訂正をしない回路で挙動を確認してみます。ベル状態を作成した後、0番の量子ビットにエラーをかけてみます。
n_qubits = 2
circ_noise = QuantumCircuit(n_qubits, 2)
circ_noise.h(0)
circ_noise.cx(0, 1)
circ_noise.append(bitphase_flip, [0])
circ_noise.measure([0, 1], [0, 1])
result_noise = backend_sim.run(circ_noise, shots=n_shots).result()
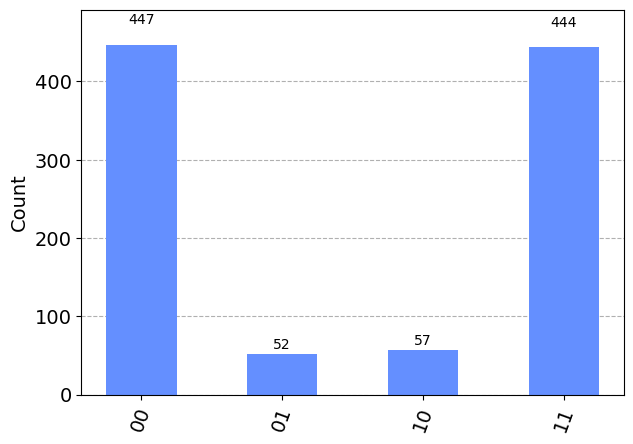
plot_histogram(result_noise.get_counts(0))
本来出現しないはずの$\lvert 01 \rangle$や$\lvert 10 \rangle$がエラーの影響により出現していることが確認できます。
位相反転エラーも起こっているのですが、サンプリングではその影響は確認できないため、ビット反転の影響のみ見えます。ここでは、片方の量子ビットのみにエラーをかけているので、エラー率は約10%になっています。
Steane符号を用いたベル状態の作成回路
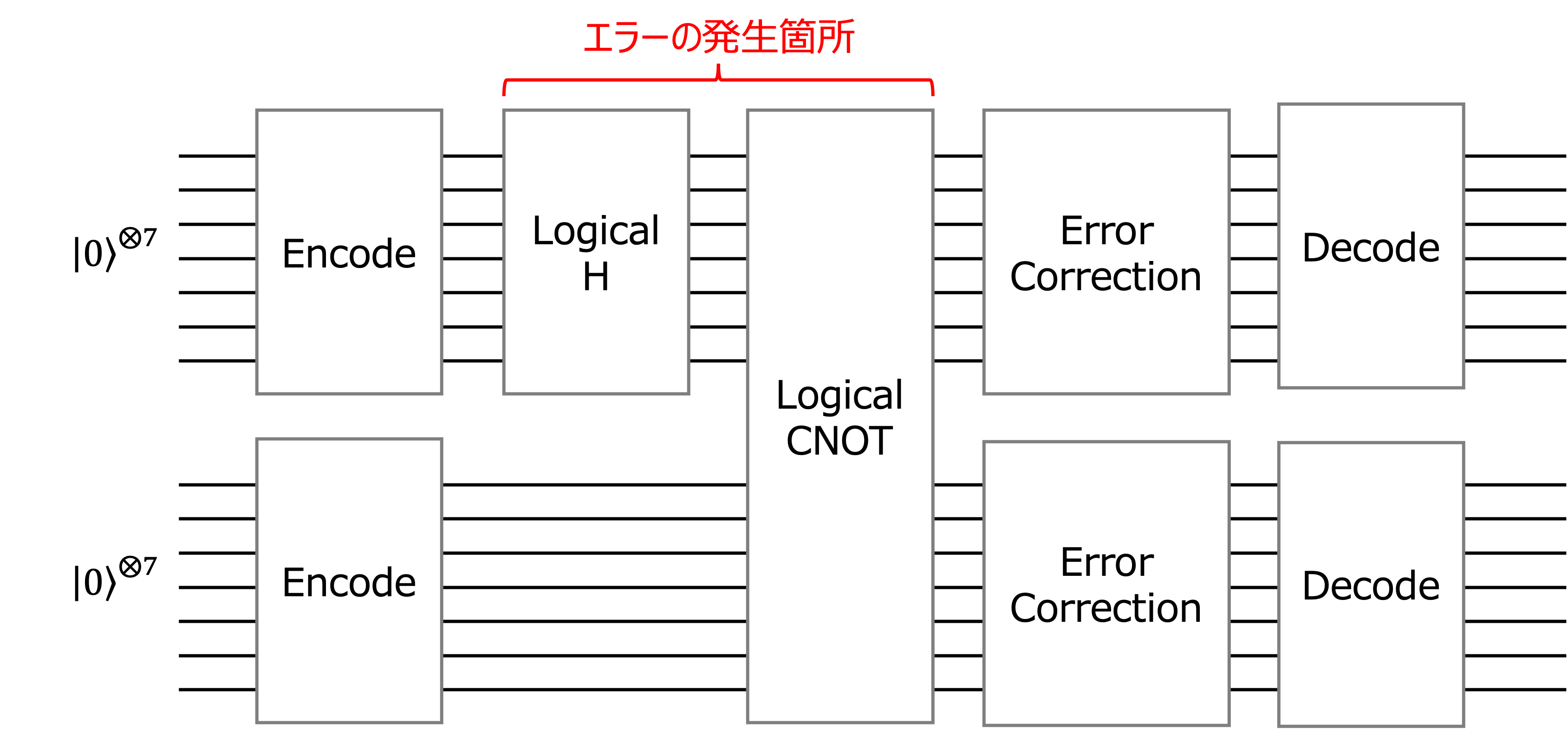
最初に、今回作成したい回路の概略図を以下に示します。
符号化された論理量子ビットに対して、論理ビット操作を用いてベル状態を作成し、エラーを訂正した上で、復号を行います。
符号化、エラー訂正、復号の操作についても、当然量子回路を用いて実装することになるのですが、この部分でのエラーの発生はないものとし、アルゴリズム部分、今回の場合はベル状態の作成部分のみでエラーが起こるものとします。
この際、各論理量子ビットにつき、1物理量子ビット以下のエラーであれば訂正できることを確認します。
この図では符号化に用いる14量子ビットのみを表示していますが、エラー訂正部分ではいくつかの補助量子ビットを利用します。ここでは、量子ビット数を抑えるため、可能な限り補助量子ビットはリセットしながら使い回します。
また、実際の誤り訂正では、シンドローム測定を行い、その結果に応じて動的に回路に訂正操作を加える形が想定することが多いですが、ここでは、マルチコントロールゲートを利用し、アンシラの状態に応じて訂正するような実装にしています。私がQiskitで動的回路の実装ができることを最近まで知らなかったので、動的回路の実装についてもそのうち勉強して、試してみたいと思います。
この回路を作成する関数を定義します。
def steane_code_bell_state(noise_channel=[], p_error=0.1):
# noise_channel : ノイズをかけたいチャネル(int)を入れたリスト
# p_error : エラーの発生確率
# エラーの定義
bitphase_flip = make_bitphase_error_channel(p_error, print_flag=False)
# 回路の記述
n_qubits = 14 + 3 # 補助量子ビットは14〜16ビット目
circ = QuantumCircuit(n_qubits, 2)
circ.barrier()
# 符号化
for i in range(2):
circ.h(0 + i*7)
circ.h(1 + i*7)
circ.h(2 + i*7)
circ.cx(3 + i*7, 4 + i*7)
circ.cx(3 + i*7, 5 + i*7)
circ.cx(2 + i*7, 3 + i*7)
circ.cx(2 + i*7, 4 + i*7)
circ.cx(2 + i*7, 6 + i*7)
circ.cx(1 + i*7, 3 + i*7)
circ.cx(1 + i*7, 5 + i*7)
circ.cx(1 + i*7, 6 + i*7)
circ.cx(0 + i*7, 4 + i*7)
circ.cx(0 + i*7, 5 + i*7)
circ.cx(0 + i*7, 6 + i*7)
circ.barrier()
# エラーチャネル
# ここで、論理アダマールゲートと論理CNOTゲートをかける
for i in range(7):
circ.h(i)
for i in range(7):
circ.cx(i, i+7)
# エラーは以下で発生させる
for i in noise_channel:
assert (0 <= i) and (i < 17)
circ.append(bitphase_flip, [i])
# エラー訂正
for i in range(2): # 論理ビット数に対応するループ
circ.barrier()
for j in range(3): # アンシラの初期化(同じものを使い回す)
circ.reset(j + 14)
circ.h(j + 14)
# アンシラに情報を送る
circ.cz(14, 0 + i*7)
circ.cz(14, 4 + i*7)
circ.cz(14, 5 + i*7)
circ.cz(14, 6 + i*7)
circ.cz(15, 1 + i*7)
circ.cz(15, 3 + i*7)
circ.cz(15, 5 + i*7)
circ.cz(15, 6 + i*7)
circ.cz(16, 2 + i*7)
circ.cz(16, 3 + i*7)
circ.cz(16, 4 + i*7)
circ.cz(16, 6 + i*7)
for j in range(3):
circ.h(j + 14)
circ.barrier()
# ビット反転
circ.x(15)
circ.x(16)
circ.mcx([14, 15, 16], 0 + i*7)
circ.x(15)
circ.x(16)
circ.x(14)
circ.x(16)
circ.mcx([14, 15, 16], 1 + i*7)
circ.x(14)
circ.x(16)
circ.x(14)
circ.x(15)
circ.mcx([14, 15, 16], 2 + i*7)
circ.x(14)
circ.x(15)
circ.x(14)
circ.mcx([14, 15, 16], 3 + i*7)
circ.x(14)
circ.x(15)
circ.mcx([14, 15, 16], 4 + i*7)
circ.x(15)
circ.x(16)
circ.mcx([14, 15, 16], 5 + i*7)
circ.x(16)
circ.mcx([14, 15, 16], 6 + i*7)
# アンシラをリセットして使い回す
circ.barrier()
for j in range(3):
circ.reset(j + 14)
circ.h(j + 14)
circ.cx(14, 0 + i*7)
circ.cx(14, 4 + i*7)
circ.cx(14, 5 + i*7)
circ.cx(14, 6 + i*7)
circ.cx(15, 1 + i*7)
circ.cx(15, 3 + i*7)
circ.cx(15, 5 + i*7)
circ.cx(15, 6 + i*7)
circ.cx(16, 2 + i*7)
circ.cx(16, 3 + i*7)
circ.cx(16, 4 + i*7)
circ.cx(16, 6 + i*7)
for j in range(3):
circ.h(j + 14)
circ.barrier()
# 位相反転
circ.x(15)
circ.x(16)
circ.h(0 + i*7)
circ.mcx([14, 15, 16], 0 + i*7)
circ.h(0 + i*7)
circ.x(15)
circ.x(16)
circ.x(14)
circ.x(16)
circ.h(1 + i*7)
circ.mcx([14, 15, 16], 1 + i*7)
circ.h(1 + i*7)
circ.x(14)
circ.x(16)
circ.x(14)
circ.x(15)
circ.h(2 + i*7)
circ.mcx([14, 15, 16], 2 + i*7)
circ.h(2 + i*7)
circ.x(14)
circ.x(15)
circ.x(14)
circ.h(3 + i*7)
circ.mcx([14, 15, 16], 3 + i*7)
circ.h(3 + i*7)
circ.x(14)
circ.x(15)
circ.h(4 + i*7)
circ.mcx([14, 15, 16], 4 + i*7)
circ.h(4 + i*7)
circ.x(15)
circ.x(16)
circ.h(5 + i*7)
circ.mcx([14, 15, 16], 5 + i*7)
circ.h(5 + i*7)
circ.x(16)
circ.h(6 + i*7)
circ.mcx([14, 15, 16], 6 + i*7)
circ.h(6 + i*7)
circ.barrier()
# 復号
for i in range(2):
circ.cx(0 + i*7, 4 + i*7)
circ.cx(0 + i*7, 5 + i*7)
circ.cx(0 + i*7, 6 + i*7)
circ.cx(1 + i*7, 3 + i*7)
circ.cx(1 + i*7, 5 + i*7)
circ.cx(1 + i*7, 6 + i*7)
circ.cx(2 + i*7, 3 + i*7)
circ.cx(2 + i*7, 4 + i*7)
circ.cx(2 + i*7, 6 + i*7)
circ.cx(3 + i*7, 4 + i*7)
circ.cx(3 + i*7, 5 + i*7)
circ.h(0 + i*7)
circ.h(1 + i*7)
circ.h(2 + i*7)
# 測定
circ.measure([3, 10], [0, 1])
return circ
見ての通り、非常に長い回路となっております。回路としてはより最適化できる部分はありますが、今回はこれを動かしてみます。
まずはエラーをかけずに動かしてみます。環境にもよりますが、実行時間が数分程度かかります。
circ = steane_code_bell_state()
# 以下のコードで回路を可視化できますが、非常に巨大になります。
# circ.draw("mpl")
# シミュレータでの実行
result_ideal = backend_sim.run(circ, shots=n_shots).result()
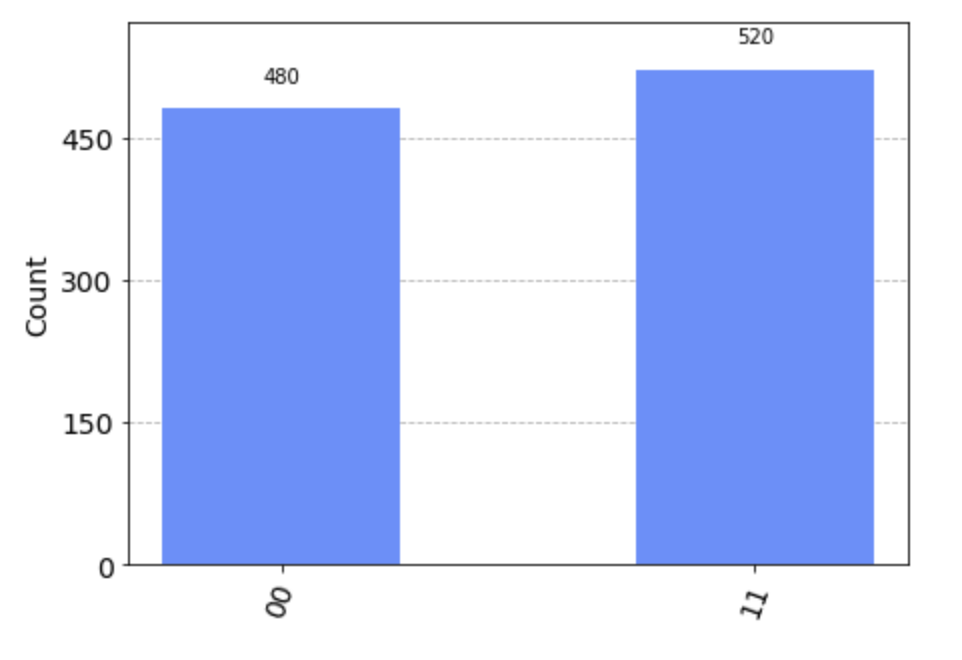
plot_histogram(result_ideal.get_counts(0))
問題なくベル状態が作れていることが確認できます。
エラーを加えてみる
今回用いたSteane符号では1論理量子ビットあたり、1物理量子ビットまでの誤りを訂正できます。
以下のコードで挙動を確認してみます。今回は、ベル状態の作成部分でエラーが発生することを想定しており、論理Hゲート、論理CNOTゲートの二つの操作が終わった後に一度だけエラーチャネルを通すような実装となっています。
より本来の挙動に近づけるのであれば、各ゲート操作ごとにエラーを加えるほうが適切ですが、特定ビットのみに誤りを加えた際の挙動をわかりやすくするため、今回このような実装にしています。
# 0番目の物理ビットにエラー
circ = steane_code_bell_state(noise_channel=[0])
result_noise = backend_sim.run(circ, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
# 3番目と10番目の物理ビットにエラー(各論理量子ビットから1物理量子ビットずつ)
circ = steane_code_bell_state(noise_channel=[3, 10])
result_noise = backend_sim.run(circ, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
# 0番目と1番目の物理ビットにエラー(一つの論理量子ビットの2物理量子ビットにエラー)
circ = steane_code_bell_state(noise_channel=[0, 1])
result_noise = backend_sim.run(circ, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
実行してみると、想定通り1,2番目では問題なくベル状態が観測され、3番目ではエラーが混ざった結果が観測されます。
エラー率を変化させてみる
実際の量子コンピュータでは、特定の量子ビットでしかエラーが発生しない、ということはなく、すべての量子ビットでエラーが発生する可能性があります。
ここでは、すべての量子ビットにエラーを加えるという条件下で、エラー発生確率を変化させることで、どのような影響が出るかを確認してみます。
最初に誤り訂正なしの場合を再度確認します。
# 誤り訂正なし
n_qubits = 2
circ_noise = QuantumCircuit(n_qubits, 2)
circ_noise.h(0)
circ_noise.cx(0, 1)
circ_noise.append(bitphase_flip, [0])
circ_noise.append(bitphase_flip, [1])
circ_noise.measure([0, 1], [0, 1])
result_noise = backend_sim.run(circ_noise, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
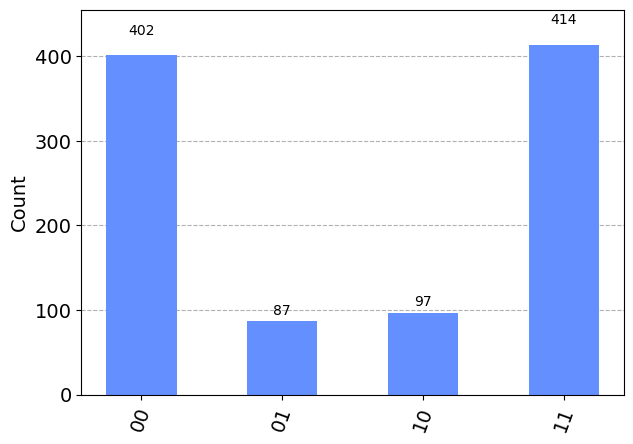
今回は両方のビットにエラーを加えているので、合計のエラー率は20%程度となります。ベル状態なので、両方の量子ビットにビット反転エラーが発生した場合は、実質的には正常な状態になる点には注意が必要です。
次に、誤り訂正ありの回路です。まずは同じエラー率10%で試してみます。
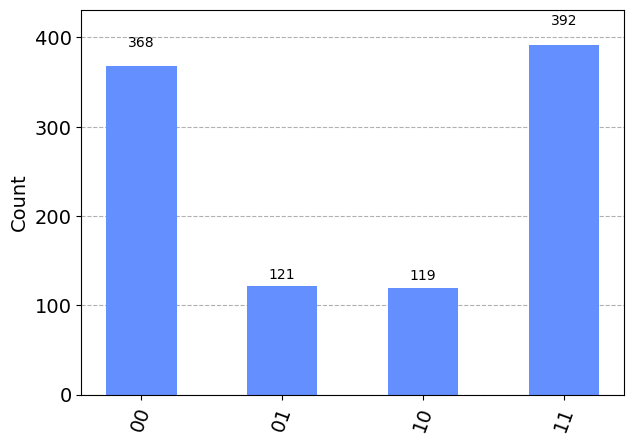
# 誤り訂正あり
circ = steane_code_bell_state(noise_channel=range(14), p_error=0.1)
result_noise = backend_sim.run(circ, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
誤り訂正なしの場合に比べて、エラー率が上がっています。これは、誤り訂正においては、各部品のエラー発生率がある閾値より低い場合は、冗長化することで、トータルのエラー発生率を抑えることができますが、逆に、閾値より高い場合は、エラーの発生確率が増してしまうためです。
簡単に言えば、7量子ビット中、2量子ビット以上でエラーが発生する確率が、単独のエラー率より高いのであれば、逆効果になります。
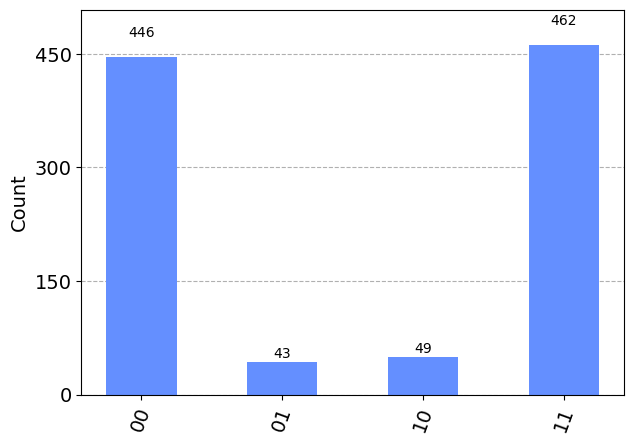
試しに、エラー発生率を5%にしてみると、冗長化によりエラー発生率が抑えられている様子が確認できると思います。
# 誤り訂正なし
bitphase_flip_005 = make_bitphase_error_channel(p_error=0.05, print_flag=False)
n_qubits = 2
circ_noise = QuantumCircuit(n_qubits, 2)
circ_noise.h(0)
circ_noise.cx(0, 1)
circ_noise.append(bitphase_flip_005, [0])
circ_noise.append(bitphase_flip_005, [1])
circ_noise.measure([0, 1], [0, 1])
result_noise = backend_sim.run(circ_noise, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
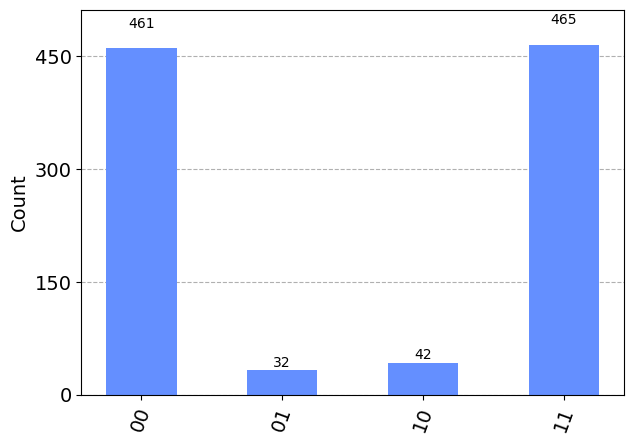
# 誤り訂正あり
circ = steane_code_bell_state(noise_channel=range(14), p_error=0.05)
result_noise = backend_sim.run(circ, shots=n_shots).result()
plot_histogram(result_noise.get_counts(0))
5%の場合、そこまで明確な差はありませんが、さらに低い確率であれば、より顕著な差が確認できます。
まとめ
今回はSteane符号を使った論理ビット操作の簡単な例として、ベル状態の作成を試してみました。
回路を可視化してみるとわかりますが、論理ビット操作自体の実装は簡単なものの、その後の誤り訂正の回路が長いです。そのため、全体で見るとベル状態を作成するだけでも、それなりの回路長になってしまいます。
今回、アルゴリズム部分でのみエラーが発生するものとして考えましたが、実際には符号化、誤り訂正、測定のすべてのプロセスでエラーが発生する可能性があり、このあたりについても考慮する必要があります。
これらのことから、非常に簡単な回路であっても、現在の量子コンピュータ実機で誤り訂正を活用して、エラーのない計算を行うことは、まだまだ難しいと考えています。
実機での誤り訂正符号を実現するためには、様々な課題がありますが、本記事を通じて論理ビット演算のイメージを理解していただければ幸いです。