はじめに
ハフモデル[1]は1963年にDavid Huffによって提案された商圏分析のモデルです。競合する店舗の存在を加味した上で、店舗の魅力度と、顧客から店舗までの距離という二つの要素に基づいて、顧客の来訪確率を計算するモデルになっています。
古典的なモデルではありますが、今日においても商圏分析のツールとして活用されることも少なくありません。
今回は、ハフモデルに基づいて、新規店舗の最適な出店箇所を簡単な最適化計算によって求めてみようと思います。
データとしては擬似データを生成して利用します。
ハフモデルの数式表現
ハフモデルの基本的な考え方としては以下の2点です。
- 顧客は魅力度が高い店舗を好む。
- 顧客は近い店舗を好む。
この考え方を確率的なモデルに落とし込んだものがハフモデルであり、顧客$i$が店舗$j$に来訪する確率$P_{i, j}$を以下の数式で定義します。
$$ P_{i,j} = \frac{\frac{A_{j}^{\alpha}}{d_{i,k}^{\beta}}}{\sum_{k=1}^{n} \frac{A_{k}^{\alpha}}{d_{i,k}^{\beta}}} $$
- $A_j$:店舗$j$の魅力度
- $d_{i, j}$:顧客$i$から店舗$j$までの距離
- $n$:店舗の総数
- $\alpha$:魅力度の影響度を決定するパラメータ
- $\beta$:距離の影響度を決定するパラメータ
簡単に言うと、「(魅力度)/(距離)」を重みとして、確率化したものになります。
問題設定
今回は以下の設定でハフモデルを考え、どの位置に店舗を出店するのが最適かを考えます。
- $100 \times 100$のグリッド状の地図を考える。左上を$(0,0)$とし、下に$y$、右に$x$移動した地点の座標を$(y, x)$とする。
- このエリアには、三つのブランドが存在しており、それぞれ三つの店舗を保有している。各店舗の所在地$(y_j, x_j)$と魅力度$A_j$は既知とする。
- 各地点$(y, x)$における潜在顧客数$m_{y, x}$については既知とする。すべての顧客はいずれか一つの店舗を利用する。
- 距離にはユークリッド距離を採用する。
- $\alpha,\beta=1$とする。
- グリッド上の任意の点に1店舗を新たに出店する。その際に、自ブランドの総獲得顧客数を最大化できる場所を探したい。
実装
今回はPythonを用いて、擬似データでの実装を行います。
まずはライブラリのインポートを行います。
import numpy as np
import random
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
%matplotlib inline
データの生成
問題設定に合わせてデータを生成します。
店舗情報の生成
最初に、各店舗の情報を作成します。
# 店舗の情報を格納する辞書、keyはブランド名、valueは店舗情報のリスト、リストの各要素は辞書で、座標と魅力度を保存
shop_dictionary = dict()
# ここではブランド名は単純に数値とする
for i in range(3):
shop_dictionary[i] = list()
# 乱数のシードを固定
random.seed(0)
np.random.seed(0)
# ランダムに店舗の座標と魅力度を決定し、辞書に保存する
for i in range(3):
for j in range(3):
shop_information = dict()
# 位置の生成
y = random.randint(5, 95) # 地図上の端は避ける
x = random.randint(5, 95)
shop_information["position"] = (y, x)
# 魅力度の生成
a = random.randint(20, 50)
shop_information["attractiveness"] = a
shop_dictionary[i].append(shop_information)
これにより以下のような店舗情報ができました。実装上は位置が被る可能性もありますが、今回は店舗数が少ない関係もあり、特にこれに対応する処理はしていません。
{0: [{'position': (54, 58), 'attractiveness': 21},
{'position': (38, 70), 'attractiveness': 35},
{'position': (56, 43), 'attractiveness': 50}],
1: [{'position': (66, 50), 'attractiveness': 38},
{'position': (32, 69), 'attractiveness': 24},
{'position': (41, 22), 'attractiveness': 44}],
2: [{'position': (17, 84), 'attractiveness': 45},
{'position': (37, 73), 'attractiveness': 42},
{'position': (82, 23), 'attractiveness': 29}]}
潜在顧客情報の生成
$100 \times 100$グリッド上の各地点の潜在顧客数を決めます。ここでは、二次元の正規分布を重ね合わせた様なものを用意することにします。
def normal_distribution(y, x, n, var, population_grid):
# y, x : 分布の中心
# n : 分布の中心の人数
# var : 分散
# population_grid : 人口情報
for _y in range(100):
for _x in range(100):
p = n*np.exp( -(1/2) * (1/var) * ((_y - y)**2 + (_x - x)**2) ) / (2 * np.pi)
population_grid[_y][_x] += int(p)
# 人数を加算した人口情報を返す
return population_grid
population_grid = np.zeros((100, 100))
# 適当なパラメータで4個の正規分布を重ねる
population_grid = normal_distribution(30, 30, 150, 128, population_grid)
population_grid = normal_distribution(55, 70, 200, 256, population_grid)
population_grid = normal_distribution(60, 40, 250, 256, population_grid)
population_grid = normal_distribution(90, 50, 200, 128, population_grid)
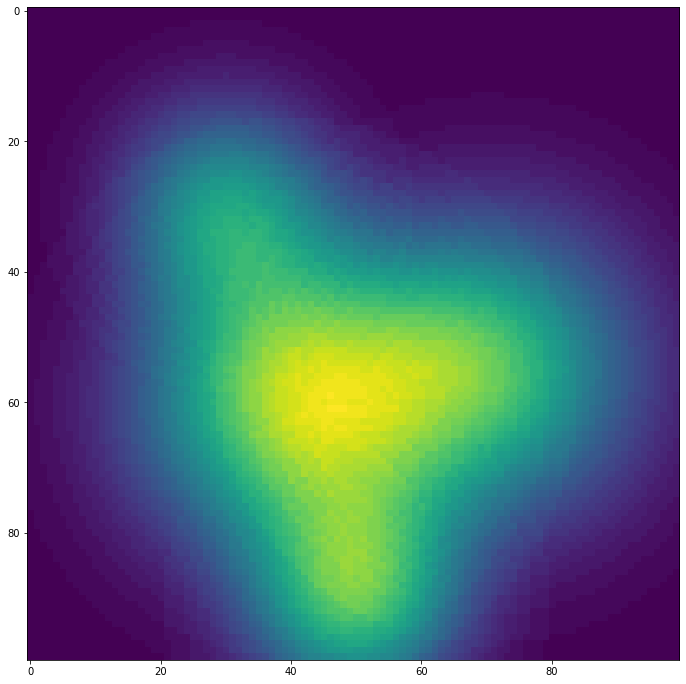
出来上がった顧客分布を可視化してみます。
plt.figure(figsize=(12, 12))
plt.imshow(population_grid)
色が明るい場所ほど人が多いことに相当します。気持ちとしては、中央からやや左下あたりが大きく栄えており、南北と東に町が続いているようなものを想定しています。
これに現在の店舗の所在地と重ねて確認してみます。
shop_location_grid = np.ones((100, 100, 3))
for i in range(3):
for j in range(len(shop_dictionary[i])):
y, x = shop_dictionary[i][j]["position"]
shop_location_grid[y][x][(i + 1) % 3] = 0
shop_location_grid[y][x][(i + 2) % 3] = 0
plt.figure(figsize=(12, 12))
plt.imshow(population_grid)
plt.imshow(shop_location_grid, alpha=0.5)
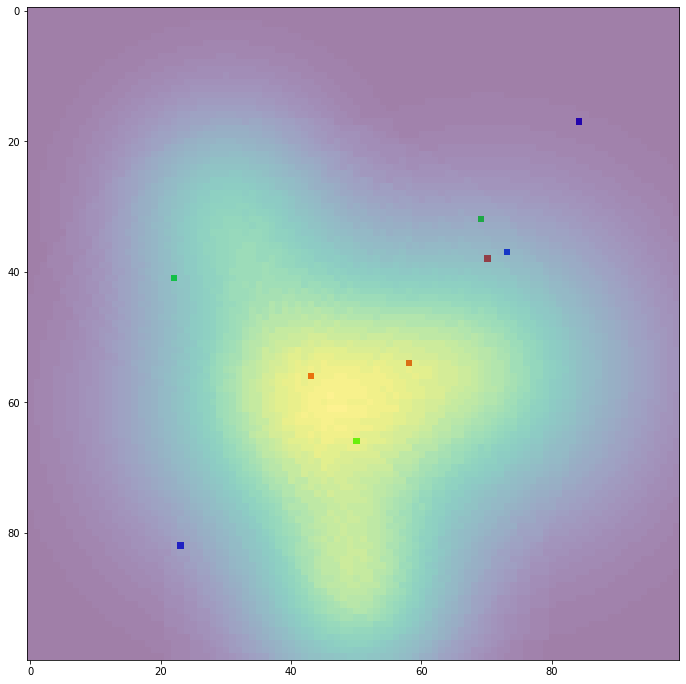
少し見づらいですが、赤、緑、青の点がそれぞれのブランドの店舗に相当します。
データの生成手順上、既存店舗の所在地がこの顧客分布に対して、現実的なのかというと、かなり怪しいのですが、実装上は問題にならないので、このまま進めます。
最適化計算の準備
最適化計算の際に使ういくつかの関数を準備しておきます。
# 2点間のユークリッド距離を計算
def euclidean_dist(y1, x1, y2, x2):
dist = np.sqrt( (y1 - y2)**2 + (x2 - x1)**2 )
return dist
# 地点(y, x)における顧客が、どのブランドを選択するかを計算
def calculate_score(y, x):
shop_score = dict()
shop_customer_count = dict()
# 各ブランドごとの合計スコアを計算
for i in shop_dictionary.keys():
score = 0
for j in range(len(shop_dictionary[i])):
shop_y, shop_x = shop_dictionary[i][j]["position"]
shop_a = shop_dictionary[i][j]["attractiveness"]
dist = euclidean_dist(y, x, shop_y, shop_x)
if dist != 0:
score += shop_a / dist
else:
score += 10**9 # 距離が0の場合には、極端に大きな値を代入
shop_score[i] = score
# 全体のスコアを計算
sum_score = 0
for i in shop_dictionary.keys():
sum_score += shop_score[i]
# 獲得顧客数を計算
for i in shop_dictionary.keys():
shop_customer_count[i] = population_grid[y][x]*(shop_score[i] / sum_score)
return shop_customer_count
# 全体として、各ブランドの利用顧客数を計算
def calculate_total_shop_customer():
total_shop_customer = dict()
for i in shop_dictionary.keys():
total_shop_customer[i] = 0
for i in range(100):
for j in range(100):
shop_customer = calculate_score(i, j)
for k in shop_dictionary.keys():
total_shop_customer[k] += shop_customer[k]
return total_shop_customer
ここでは最終的に自ブランドの集客数を最大化することを目的としているため、ブランドごとの集客数を出力するようにしており、店舗単位の情報は切り落としてます。
各ブランドの利用顧客数の計算量は、グリッドの一辺の長さを$D$とすると、$\mathrm{O}(nD^2)$となります。
現時点での各ブランドの獲得顧客数を確認すると以下のようになっています。
calculate_total_shop_customer()
# {0: 53758.39058228922, 1: 49916.300852671375, 2: 37918.30856503919}
出店位置の計算
ここでは、自ブランドとして、0番のブランド(地図上の赤色)を想定し、魅力度30の店を新たに作ることとします。魅力度は位置に限らず一定とします。
単純な全探索をする場合、$D \times D$の各候補地に対して、出店したと仮定して、先ほどの獲得顧客数計算を繰り返し行えばよいので、トータルで$\mathrm{O}(nD^4)$のコストとなります。今回、$n=10, D=100$程度のオーダーなので、全探索でも現実的な時間で解くことはできます。
とはいえ、今回はC++などの高速な言語ではなく、全てPythonで実装していることもあり、かなり計算が遅いため、近似的な解法を試します。
今回の問題設定は離散最適化ではありますが、分布の形状から勾配法のような手法が有効そうなので、これをベースに実装します。
まず最初に適当な座標を入力して、新たな店舗情報を追加します。
shop_information = dict()
y = 0
x = 0
shop_information["position"] = (y, x)
a = 30
shop_information["attractiveness"] = a
# ブランド0の一番最後に新規店舗の情報を追加
shop_dictionary[0].append(shop_information)
次に勾配を計算する関数を実装します。先述の通り、離散最適化なので、微少量を変化させて勾配を計算することができないので、±1の地点の情報を用いて、その差分を勾配とみなします。
すなわち、以下の式で定義します。
$$ \frac{\partial f(y, x)}{\partial y} = \frac{f(y+1, x) - f(y-1,x)}{2}$$
$$ \frac{\partial f(y, x)}{\partial x} = \frac{f(y, x+1) - f(y,x-1)}{2}$$
def calc_grad(y, x):
# 新規店舗(ブランド0の一番最後の店舗)の座標を入力に勾配を計算
shop_dictionary[0][-1]["position"] = (y+1, x)
y_plus_score = calculate_total_shop_customer()[0]
shop_dictionary[0][-1]["position"] = (y-1, x)
y_minus_score = calculate_total_shop_customer()[0]
shop_dictionary[0][-1]["position"] = (y, x+1)
x_plus_score = calculate_total_shop_customer()[0]
shop_dictionary[0][-1]["position"] = (y, x-1)
x_minus_score = calculate_total_shop_customer()[0]
y_grad = (y_plus_score - y_minus_score) / 2
x_grad = (x_plus_score - x_minus_score) / 2
return y_grad, x_grad
あとはランダムな点を始点として、勾配計算を元に座標を更新していきます。
best_score_records = []
for iteration in tqdm(range(5)): # 試行回数
print(f"iteration:{iteration}")
best_score = 0
best_y = 0
best_x = 0
# 初期点をランダムに取る。
# 端は除外(最適値にはならないのと、勾配計算に支障があるので)
y = random.randint(1, 98)
x = random.randint(1, 98)
print(f"start pos:{y} {x}")
for i in tqdm(range(30)):
if i < 10:
lr = 1/4
elif i < 20:
lr = 1/8
else:
lr = 1/12
# スコア計算
shop_dictionary[0][-1]["position"] = (y, x)
current_score = calculate_total_shop_customer()[0]
if current_score > best_score:
print(f"{i} pos:{y} {x} score:{current_score}")
best_score = current_score
best_y = y
best_x = x
# 勾配計算
y_grad, x_grad = calc_grad(y, x)
if int(y_grad * lr) == 0 and int(x_grad * lr) == 0:
break
y += int(y_grad * lr)
x += int(x_grad * lr)
best_score_records.append([best_score, best_y ,best_x])
print(f"best score:{best_score} pos:{(best_y, best_x)}")
print(f"------------------")
ここでは、勾配が座標をずらしたときの獲得顧客数の変化に相当するので、それなりに大きい値を取ります。更新量が適切になるように、変化率のパラメータを適当に設定しています。
5回の試行で得られた結果は以下のとおりでした。
# 目的関数値、y座標、x座標
[[63411.93278134413, 74, 49],
[63411.93278134413, 74, 49],
[63411.77779348922, 74, 50],
[63411.77779348922, 74, 50],
[63411.93278134413, 74, 49]]
全探索を試してみたところ、(74, 49)が最適解だったため、60%の確率で最適解が得られていることがわかります。残りの2回も最適解の近傍にはいるので、少しパラメータをいじったり、アルゴリズムを改良すれば到達できるとは思います。
今回のケースでは、既存店舗数が少ないため、安定して最適解周辺が得られましたが、店舗数を増やして実験してみると、局所解にはまるケースも出てきたので、状況によっては、試行回数を多めにとったり、アルゴリズム自体にもう少し工夫が必要になると思います。
今回の解法では、離散最適化として考えているため、勾配計算における変数のシフト量が大きく、解の更新量も整数にしています。
店舗の座標に連続値を入れても今までの関数はすべて動くので、連続最適化として解いてから、最後に近傍の格子点を確認するような方法も良いかもしれません。
最後に、今回見つけた最適な出店位置を地図上で確認してみます。
赤色の一番下にある点が今回見つけた点です。赤色は元々良い位置を抑えられていることもあり、視覚的にも妥当な出店位置のように見えます。
まとめ
今回はハフモデルにおける最適出店地計画問題を解いてみました。今回の問題設定では、簡単な近似アルゴリズムでも問題なく十分な精度の解が得られることがわかりました。
今回のように、ライブラリを使わず、ほとんどの処理を自分で記述するのであれば、おそらくPythonよりもC++等を使ったほうが速度面では良いと思います。
また、今回の記事では最適化部分に焦点をあてましたが、実務においてこのような手法を用いる場合には、最適化計算そのものよりも、問題の設定や入力に相当するデータをどれだけ良くビジネスに当てはまるものにできるかが非常に重要かつ難しいポイントになると考えています。
例えば、魅力度については、自店舗だけでなく、競合店舗についても観測可能で、定量化可能なものである必要があります。また、距離についても、人間の移動はユークリッド距離的な直線的な移動ではありません。マンハッタン距離を用いたり、実際の道路情報などを用いることも考えられます。
それ以外にも、潜在顧客は、顧客属性にも依存するため、単純な人口分布と一致するものではないこと、$\alpha,\beta$のパラメータの決め方など、考え始めるとキリがないです。このあたりは、求める品質と作業の手間との兼ね合いの中で、モデルが役立つのかを判断することになると思います。