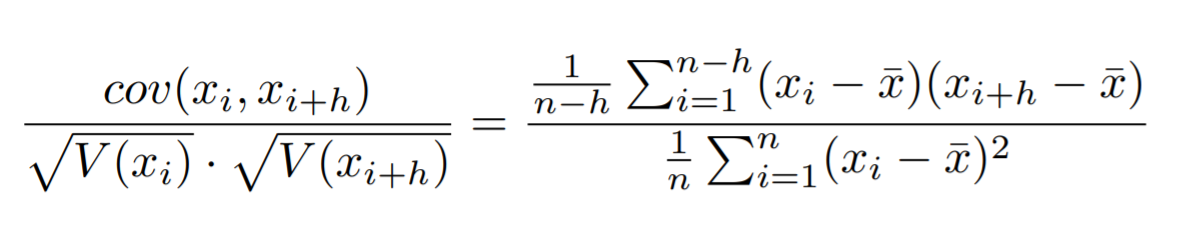はじめに
この記事では、私が自己相関係数および自己共分散を視覚的に理解した方法を紹介します。
時系列データ分析を勉強している際に、始めは自己相関係数の式がいまいち理解できず図を描いて考えてみたところ理解が捗ったので、その図を使って説明していきます。
自己相関係数の定義
分子
分子は、i時点の確率変数**x_iと、h時点だけずらしたi+h時点の確率変数x_{i+h}**の共分散、つまり自己共分散です。
右辺において、「なぜ**n-h**が出てくるんだろう?」というのが当初の私の疑問点でした。
分母
分母は、i時点の確率変数**x_iの標準偏差と、h時点だけずらしたi+h時点の確率変数x_{i+h}**の標準偏差の積です。
どうやら自己標準偏差という言葉は存在しないらしく、右辺は通常の確率変数**x_i**の分散となっています。
h時点ずらして乗算を行っているのに、「なぜラグの影響が分母に反映されていないんだろう?」というのが私の当初の疑問でした。
視覚的に説明
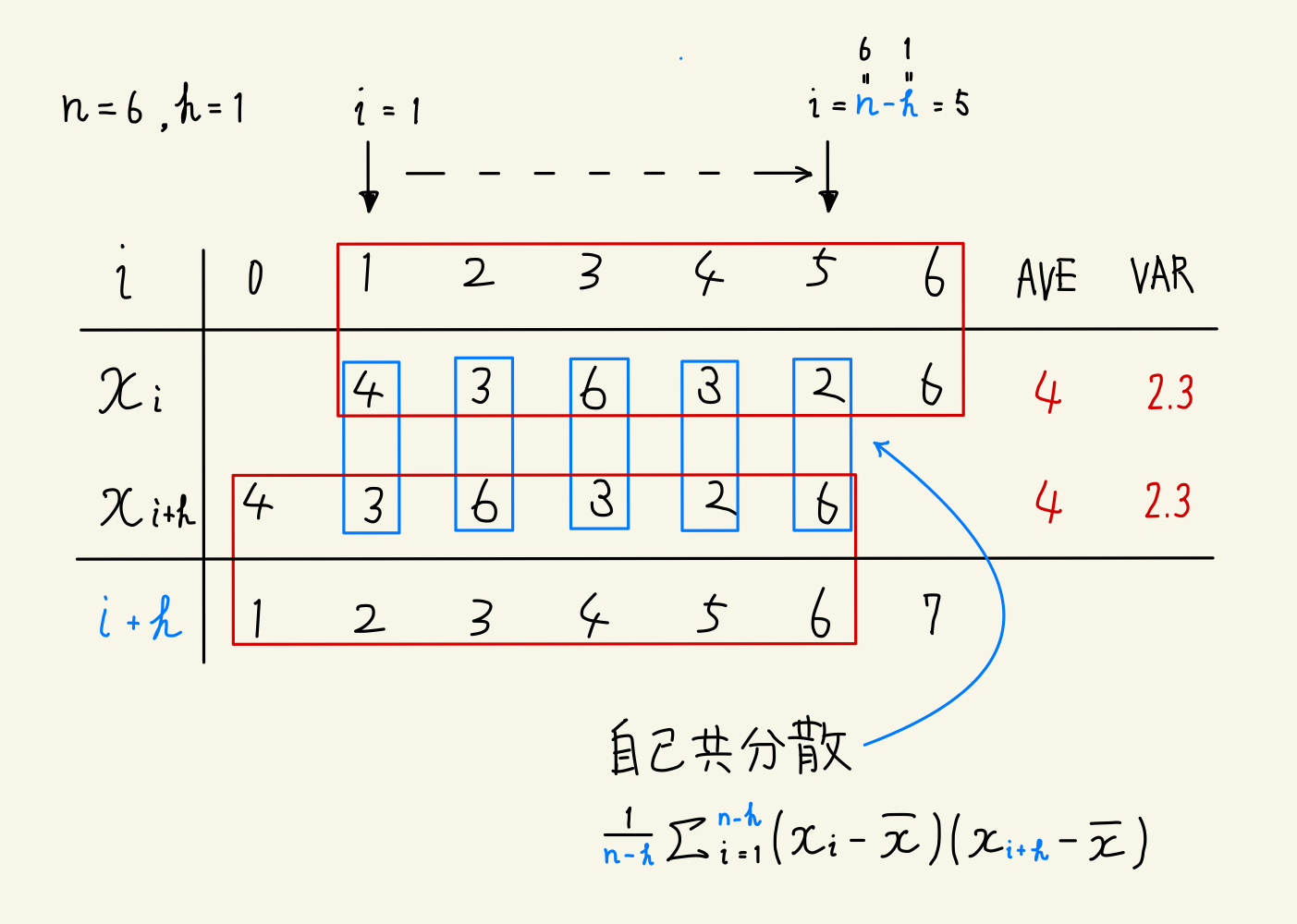
ここでは、サンプル数としてn=6、ラグとしてh=1のデータを使って説明を行います。
分子
自己相関係数の分子となっている自己共分散を考える際には、図中の青色に注目します。
確率変数**x_iをh時点ずらしてみると、x_iとx_{i+h}が重なるのはi=1からi=n-hの間(※1)の**n-h個(※2)のデータとなります。
※1. この範囲でΣによって総和を取得する
※2. データの個数で割り算する
分母
自己相関係数の分母となっている分散を考える際には、図中の赤色に注目します。
実は、確率変数**x_iも確率変数x_{i+h}もデータの値と個数が変わっていないため、両確率変数の標準偏差の積は、確率変数x_iの分散と等しい(確率変数x_{i+h}**の分散とも等しい)。
書籍が間違っているのか??
現場ですぐ使える時系列データ分析~データサイエンティストのための基礎知識~を読んでいるのですが、「自己相関係数の分子となる自己共分散って総和**Σに対して1/nじゃなくて1/(n-h)**が乗算されてないと間違っていないか??」と思っています。
統計学入門 (基礎統計学Ⅰ)を読んでみたら**1/(n-h)**が乗算されていたので、こっちの本に合わせて理解するようにしました。
最後に
分からないことがあれば図で考えてみると理解が進むのは、どんな事柄でも共通のようです。
記事に対して指摘事項等がございましたら、Qiitaコメント欄でもTwitter@kazukiigetaでも、ご連絡をいただけると嬉しいです。