離散対数問題
離散対数問題とは?
ある計算の結果から簡単に逆算ができないような数学上の問題の一つで、整数のべき乗を素数で割った余りを求める計算を用いるもの。公開鍵暗号やデジタル署名(電子署名)の アルゴリズム の基礎として応用されている。
どんな問題?
ある素数$p$について、$p$未満の自然数$g$および$x$を選択し、$g$の$x$乗を$p$で割った余り$m$を算出する。このとき、$p,g,x$から$m$は容易に算出できる一方、$g,p,m$が分かっても、このような関係を満たす$x$を求める効率的な方法は見つかっていない。
$$
g^x\equiv m\pmod p
$$
定義
$G$を位数$|G|$が有限な巡回群とする。このとき、与えられた$G$の生成元$g$と$h\in G$に対して、$g^x=h$となる整数$x(0\le x<|G|)$を求める問題。
また、このような$x$のことを$g$を底とする$h$の離散対数という。
例題
素数 $p=9973$ を用いて、 $G$ を素体 $\mathbb{Z_{9973}}$ 、生成元 $g$ を $2$ とする。
$$
\begin{align}
x=2^{555} \pmod{9973}\tag{1}\\
2^x\pmod{9973} = 1248\tag{2}
\end{align}
$$
式(1)は $2^{555}=2^{512}\cdot2^{32}\cdot2^8\cdot2^2\cdot2^1$ に変形し、 $2^{2^n}\pmod{9973}$ を求めることで比較的簡単に求まる。(バイナリ法、高速べき乗演算)
$$
2^{555}\equiv8505\cdot5089\cdot256\cdot4\cdot2\equiv3140\pmod{9973}
$$
計算式
-
$2^1,2^2,...,2^{512}\pmod p$を求める
$2^1\equiv2\pmod{9973}$
$2^2\equiv4\pmod{9973}$
$2^4\equiv16\pmod{9973}$
$2^8\equiv256\pmod{9973}$
$2^{16}\equiv256^2\equiv5698\pmod{9973}$
$2^{32}\equiv5698^2\equiv5089\pmod{9973}$
$2^{64}\equiv5089^2\equiv8013\pmod{9973}$
$2^{128}\equiv8013^2\equiv1995\pmod{9973}$
$2^{256}\equiv1995^2\equiv798\pmod{9973}$
$2^{512}\equiv798^2\equiv8505\pmod{9973}$ -
$2^{555}=2^{512}\cdot2^{32}\cdot2^8\cdot2^2\cdot2^1$より、
$2^{555}\equiv8505\cdot5089\cdot256\cdot4\cdot2\equiv3140\pmod{9973}$
計算量は、1.のべき乗剰余の演算が10回、2.の掛け算が4回。
一般に、$g^{p-1}\equiv1\pmod p$(フェルマーの小定理)を利用すれば、べき乗は$g^{p-2}\pmod p$まで求めれば良いので、1.と2.の演算は $\log_2{(p-2)}$回以下で済む。
しかし(2)の$x$を求めるには、しらみづぶしに計算する必要があるため、とても時間がかかる。
なぜなら、$g=2$は$\mathbb{Z}_{9973}$の原始元なので、$1\le x\le 9972$の範囲において$2^x\pmod{9973}$はすべて異なる値を取る。
共通鍵暗号方式(対称鍵暗号方式)
- 暗号化と復号に同じ鍵を使用する暗号方式
- この方式では、事前に情報をやりとりする相手と共通鍵を共有しておく必要がある。
- 盗聴の可能性のある通信経路を使って、どのように鍵を通信相手に配送するか→ 鍵配送問題
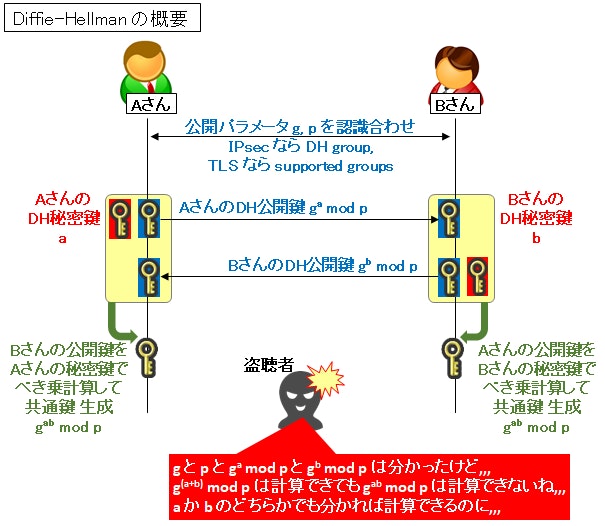
Diffie-Hellman鍵交換(DH法)
- 1976年にDiffieとHellmanによって考案
- 離散対数問題の困難性を利用した鍵交換(鍵共有)のアルゴリズム
アルゴリズム
-
素数 $p$ と $\mathbb{Z}_p$ の1つの原始元 $g$ が、あらかじめ公開されているとする。
-
通信者の2人(A,B)の各パラメータを次のように定める
- $k_A$:Aが定めた整数の乱数、Aが秘密情報として保持(秘密鍵)
- $k_B$:Bが定めた整数の乱数、Bが秘密情報として保持(秘密鍵)
- $g^{k_A}\equiv c_A\pmod p$:Aが送信する情報(公開鍵)
- $g^{k_B}\equiv c_B\pmod p$:Bが送信する情報(公開鍵)
注: $k_A,k_B$ は $2$ から $p-2$までのの整数
$k=1$のとき、 $c=g^1=g$ となるが、この $g$ は公開されているパラメータなので、 $k=1$ であることが盗聴者はわかってしまう。
$k=p-1$ のとき、 $c=g^{p-1}\equiv1\pmod p$ フェルマーの小定理より $k=p-1$であることがわかる。 -
このとき、次の手順により各々が共通鍵を取得することができる。
- A:$(c_B)^{k_A}\equiv(g^{k_B})^{k_A}\equiv g^{k_Ak_B}\equiv K_{AB}\pmod p$
- B:$(c_A)^{k_B}\equiv(g^{k_A})^{k_B}\equiv g^{k_Ak_B}\equiv K_{AB}\pmod p$
ここで、盗聴者が共通鍵 $K_{AB}$ を得るために、Aの公開鍵 $c_A$ から秘密鍵 $k_A$ を求めようとする場合、
$$
g^{k_A}\equiv c_A\pmod p
$$
を満たす整数 $k_A$ を求めることになるので、これは乗法に関する巡回群 $\mathbb{Z}_p^*$ 上における離散対数問題を解くことにほかならない。
Diffie-Hellman鍵交換の図解
【図解】素数とDiffie-Hellman鍵交換法 ~わかりやすい計算例とシーケンス,RFCや種類,アルゴリズムについて~
計算の具体例
- 素数 $p$: $1237$(本来は
300600桁以上の大きい素数を使用) - 原始元 $g$: $7\in\mathbb{Z_{1237}^*}$
- Aが定めた乱数 $k_A$: $659$
- Bが定めた乱数 $k_B$: $1234$
このとき公開鍵は
-
Aの公開鍵 $c_A$
$g^{k_A}=7^{659}=7^{(512+128+16+2+1)}\equiv51\cdot393\cdot432\cdot49\cdot7\equiv534\pmod{1237}$
-
Bの公開鍵 $c_B$
$g^{k_B}=7^{1234}=7^{(1024+128+64+16+2)}\equiv127\cdot393\cdot592\cdot432\cdot49\equiv101\pmod{1237}$
-
途中式
$7^1\equiv 7\pmod{1237}$
$7^2\equiv 49\pmod{1237}$
$7^4\equiv 49^2\equiv1164\pmod{1237}$
$7^8\equiv 1164^2\equiv381\pmod{1237}$
$7^{16}\equiv 381^2\equiv432\pmod{1237}$
$7^{32}\equiv 432^2\equiv1074\pmod{1237}$
$7^{64}\equiv 1074^2\equiv592\pmod{1237}$
$7^{128}\equiv 592^2\equiv393\pmod{1237}$
$7^{256}\equiv 393^2\equiv1061\pmod{1237}$
$7^{512}\equiv 1061^2\equiv51\pmod{1237}$
$7^{1024}\equiv 51^2\equiv127\pmod{1237}$
-
共通鍵は
$g^{k_Ak_B}=(534)^{1234}=(101)^{659}\equiv90\pmod{1237}$
$K_{AB}=90$
盗聴者の計算量
前述の通り、盗聴して共通鍵を作り出すには、公開されている情報
- 素数 $p$
- 原始元 $g\in\mathbb{Z_{p}^*}$
- A,Bの公開鍵 $c_A,c_B$
から下の関係式を用いて、秘密鍵 $k_A$ $k_A$$k_B$を求めなければならない。
$$
g^{k_A}\equiv c_A\pmod p
$$
ブルートフォース攻撃の場合、$g^2,g^3,g^4,...g^{p-2}$の最大 $p-3$ 回計算しなければならない。
したがって計算量は $O(p)$ となる。
共通鍵のビット数に対しては指数時間の計算量である。
-
指数時間である理由
- 共通鍵のビット数に応じた計算量を考える
- 簡単のため素数 $p$ ではなく、 素数べき $2^n$と有限体$F_{2^n}$を用いる
$$
g^{k_A}\equiv c_A\pmod{2^n}
$$- $F_{2^n}={0,1,g^1,g^2,...,g^{2^n-2}}$ より、共通鍵の空間の大きさは位数 $|F_{2^n}|=2^n$と同じ
- したがって、$n$は共通鍵のビット数になる
ブルートフォース攻撃より効率の良い解法は提案されているが、多項式時間で解けるものは今のところ存在しない。
ただし、量子コンピュータ上で動作する効率的な量子アルゴリズムは存在する。
中間者攻撃(MitM: Man in the Middle)
AさんとBさんの通信路の中間にいて通信に能動的に関与する中間攻撃者を考える。
- 中間攻撃者はAさんとBさんの偽の秘密鍵を作る
- AさんにはBさんの偽の公開鍵を、BさんにはAさんの偽の公開鍵を送る
- Aさんと中間攻撃者、Bさんと中間攻撃者の間で共通鍵が作られる
このときAさんと中間攻撃者、Bさんと中間攻撃者の間でしか通信が行われないため
- AさんとBさんは通信相手が中間攻撃者だと気づけない(なりすまし)
- 中間攻撃者はAさんとBさんのメッセージを復号できる(盗聴)
- 中間攻撃者はAさんとBさんのメッセージを書き換えることができる(改ざん)
対策として、公開鍵に対してデジタル署名を付加し、相手を認証してから共通鍵を作る仕組みが取られている。
参考