JPEG画像の中をちょっとだけのぞいてみる

この記事はYahoo! JAPAN 18 新卒 Advent Calendar 2018 22日目の記事です。
前回はManaka TAKAHASHIさんの「仕事のがんばり具合を記録して可視化する（記録する編）」でした。

突然ですが、みなさんが普段使っているJPEG画像の中には、実際にはどんな情報が隠れているのでしょうか？
今回は、JPEGの中で、どのような仕組みで情報を保持しているのかを、バイナリからバラして一部紹介してみようと思います。

JPEG全体の構造

JPEGをバイナリで見ると

まずは、JPEGファイルをバイナリに直してみます。

長いのでたたみます

利用したファイル：profile.jpg 

$ xxd profile.jpg
00000000: ffd8 ffe0 0010 4a46 4946 0001 0100 0001  ......JFIF......
00000010: 0001 0000 ffe2 02a0 4943 435f 5052 4f46  ........ICC_PROF
00000020: 494c 4500 0101 0000 0290 6c63 6d73 0430  ILE.......lcms.0
00000030: 0000 6d6e 7472 5247 4220 5859 5a20 07e1  ..mntrRGB XYZ ..
00000040: 0001 0019 0004 000c 0029 6163 7370 4150  .........)acspAP
00000050: 504c 0000 0000 0000 0000 0000 0000 0000  PL..............
00000060: 0000 0000 0000 0000 0000 0000 f6d6 0001  ................
00000070: 0000 0000 d32d 6c63 6d73 0000 0000 0000  .....-lcms......
00000080: 0000 0000 0000 0000 0000 0000 0000 0000  ................
00000090: 0000 0000 0000 0000 0000 0000 0000 0000  ................
000000a0: 0000 0000 0000 0000 000b 6465 7363 0000  ..........desc..
000000b0: 0108 0000 0038 6370 7274 0000 0140 0000  .....8cprt...@..
000000c0: 004e 7774 7074 0000 0190 0000 0014 6368  .Nwtpt........ch
000000d0: 6164 0000 01a4 0000 002c 7258 595a 0000  ad.......,rXYZ..
000000e0: 01d0 0000 0014 6258 595a 0000 01e4 0000  ......bXYZ......
000000f0: 0014 6758 595a 0000 01f8 0000 0014 7254  ..gXYZ........rT
00000100: 5243 0000 020c 0000 0020 6754 5243 0000  RC....... gTRC..
00000110: 022c 0000 0020 6254 5243 0000 024c 0000  .,... bTRC...L..
00000120: 0020 6368 726d 0000 026c 0000 0024 6d6c  . chrm...l...$ml
00000130: 7563 0000 0000 0000 0001 0000 000c 656e  uc............en
00000140: 5553 0000 001c 0000 001c 0073 0052 0047  US.........s.R.G
00000150: 0042 0020 0062 0075 0069 006c 0074 002d  .B. .b.u.i.l.t.-
00000160: 0069 006e 0000 6d6c 7563 0000 0000 0000  .i.n..mluc......
00000170: 0001 0000 000c 656e 5553 0000 0032 0000  ......enUS...2..
00000180: 001c 004e 006f 0020 0063 006f 0070 0079  ...N.o. .c.o.p.y
00000190: 0072 0069 0067 0068 0074 002c 0020 0075  .r.i.g.h.t.,. .u
000001a0: 0073 0065 0020 0066 0072 0065 0065 006c  .s.e. .f.r.e.e.l
000001b0: 0079 0000 0000 5859 5a20 0000 0000 0000  .y....XYZ ......
000001c0: f6d6 0001 0000 0000 d32d 7366 3332 0000  .........-sf32..
000001d0: 0000 0001 0c4a 0000 05e3 ffff f32a 0000  .....J.......*..
000001e0: 079b 0000 fd87 ffff fba2 ffff fda3 0000  ................
000001f0: 03d8 0000 c094 5859 5a20 0000 0000 0000  ......XYZ ......
00000200: 6f94 0000 38ee 0000 0390 5859 5a20 0000  o...8.....XYZ ..
00000210: 0000 0000 249d 0000 0f83 0000 b6be 5859  ....$.........XY
00000220: 5a20 0000 0000 0000 62a5 0000 b790 0000  Z ......b.......
00000230: 18de 7061 7261 0000 0000 0003 0000 0002  ..para..........
00000240: 6666 0000 f2a7 0000 0d59 0000 13d0 0000  ff.......Y......
00000250: 0a5b 7061 7261 0000 0000 0003 0000 0002  .[para..........
00000260: 6666 0000 f2a7 0000 0d59 0000 13d0 0000  ff.......Y......
00000270: 0a5b 7061 7261 0000 0000 0003 0000 0002  .[para..........
00000280: 6666 0000 f2a7 0000 0d59 0000 13d0 0000  ff.......Y......
00000290: 0a5b 6368 726d 0000 0000 0003 0000 0000  .[chrm..........
000002a0: a3d7 0000 547b 0000 4ccd 0000 999a 0000  ....T{..L.......
000002b0: 2666 0000 0f5c ffdb 0043 0005 0304 0404  &f...\...C......
000002c0: 0305 0404 0405 0505 0607 0c08 0707 0707  ................
000002d0: 0f0b 0b09 0c11 0f12 1211 0f11 1113 161c  ................
000002e0: 1713 141a 1511 1118 2118 1a1d 1d1f 1f1f  ........!.......
000002f0: 1317 2224 221e 241c 1e1f 1eff db00 4301  .."$".$.......C.
00000300: 0505 0507 0607 0e08 080e 1e14 1114 1e1e  ................
00000310: 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e  ................
00000320: 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e  ................
00000330: 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e 1e1e  ................
00000340: ffc0 0011 0800 1900 1903 0122 0002 1101  ..........."....
00000350: 0311 01ff c400 1700 0003 0100 0000 0000  ................
00000360: 0000 0000 0000 0000 0306 0705 ffc4 0037  ...............7
00000370: 1000 0102 0402 0408 0f00 0000 0000 0000  ................
00000380: 0002 0103 0004 0511 0621 0712 4151 2431  .........!..AQ$1
00000390: 4261 7181 91c1 1517 2223 3233 3435 5253  Baq....."#2345RS
000003a0: 5492 94d2 e1ff c400 1701 0100 0300 0000  T...............
000003b0: 0000 0000 0000 0000 0000 0503 0407 ffc4  ................
000003c0: 0024 1100 0104 0103 0305 0000 0000 0000  .$..............
000003d0: 0000 0001 0002 0304 1105 1271 2131 6106  ...........q!1a.
000003e0: 1351 92c1 ffda 000c 0301 0002 1103 1100  .Q..............
000003f0: 3f00 ae52 74cd 4a96 70e5 9ca5 d51e 4055  ?..Rt.J.p.....@U
00000400: 1354 40b6 4b6f 8b9a 0758 d30e 1a71 c718  .T@.Ko...X...q..
00000410: 2a45 5adc 57f3 7654 dfe9 444a a0e1 a4eb  *EZ.W.vT..DJ....
00000420: ceb0 5aa0 2e9a 6aa7 22e4 bc7b efbe 0731  ..Z...j."..{...1
00000430: 775e 79b5 ccc5 c220 e7cf 34ef eddf 0ccb  w^y.... ..4.....
00000440: e99a 369a d128 38e4 e41e 506d d466 6021  ..6..(8...Pm.f`!
00000450: a550 66f1 d515 f7f8 3cbd 5075 9724 510f  .Pf.....<.Pu.$Q.
00000460: da34 3c31 4efa e77e dfec 4a3d 5cb9 1f28  .4<1N..~..J=\..(
00000470: d150 7993 6af7 76c3 5754 59b7 5057 6b5b  .Py.j.v.WTY.PWk[
00000480: 1388 1e70 7b63 e423 9b52 095c 5cf6 f5e4  ...p{c.#.R.\\...
00000490: 8fd5 bf5c c292 54e9 d709 646c 4a4a ab77  ...\..T...dlJJ.w
000004a0: 0f3b ae7b 6054 9a2e 1d98 9ae1 7204 86a5  .;.{`T......r...
000004b0: ad70 7cc7 3bec ce28 da4e f783 dd2b 13b6  .p|.;..(.N...+..
000004c0: 3dac 7a63 35b1 aa5e 8262 04ce fb15 3581  =.zc5..^.b....5.
000004d0: ed4b 81d9 3e51 b475 806a 79bf 2132 8449  .K..>Q.u.jy.!2.I
000004e0: 6f26 71c4 44ea bc33 78ae c1bf 21ff 00cb  o&q.D..3x...!...
000004f0: 38c8 c1dc 8879 86a1 b934 f18d ef3d 3c94  8....y...4...=<.
00000500: cd7d 85b9 da17 ffd9                      .}......

これだけでは、何が書いてあるのか判別は難しいですね。
では、初めから読んでいきます。

簡単な全体像

JPEGファイルの全体的な構造は、図説すると以下のようになります。

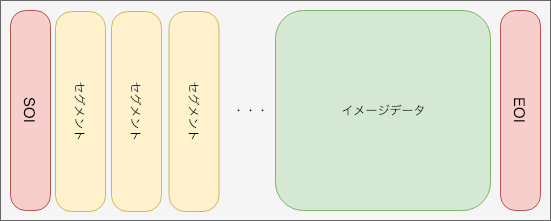
JPEGはマーカと呼ばれるもので分割されています。マーカは2バイトのデータで、1バイト目は必ずffで始まります。
ファイルの最初と最後にあるのが、スタートマーカと呼ばれるffd8とエンドマーカと呼ばれるffd9です。
上記のバイナリでもそうであるように、遍くJPEGは始まりと終わりをこの二つのマーカで区切っており、ファイルの判定基準の一つとなっています。

バイナリ	コード	名前	概要
ffd8	SOI	スタートマーカ	JPEGの始まりを示す
ffd9	EOI	エンドマーカ	JPEGの終わりを示す

この二つのマーカに挟まれた間に、複数のセグメントとイメージデータが存在しています。
このセグメントについて、次の項で説明していきます。

セグメント

セグメントとは、JPEG画像内部で保持しているさまざまな情報について、その種類ごとにまとめたものです。

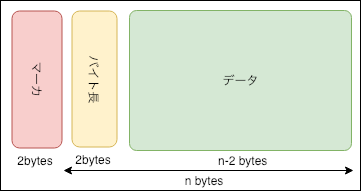
まず先頭に、セグメントの種類を示すマーカが存在します。続いてセグメントのマーカを除いた長さを2バイトの数値で示し、最後にそのセグメントで保持する情報が続きます。

今回は、何種類かあるもののうち、画像の表示に必須なもののみを紹介していきます。

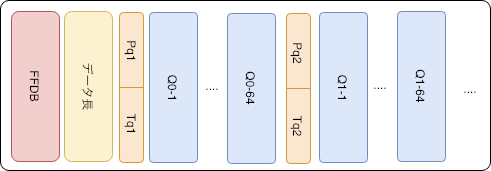
DQT

量子化テーブルの定義（Define Quantization Table）
JPEGではデータの圧縮時に量子化を用いた削減を行います。その量子化係数を保存したテーブルです。
始点となるマーカはffdbです。
一つのセグメントで複数個のテーブルの定義を行え、各テーブルごとの識別番号や、量子化係数64個の定義をしています。また、複数の量子化テーブルを定義し、一つのセグメントで一つのテーブルを定義することもできます。

DHT

ハフマンテーブルの定義（Define Huffman Table）
おそらく（個人的には）JPEG圧縮を理解する上で一番ややこしい箇所です。
マーカはffd4です。
JPEG画像は圧縮する上でハフマン圧縮を用いています。ハフマン符号について詳しい説明は省きますが、簡単に言うと頻出するデータほど短いコードを、あまり出現しないデータに長いコードを割り当ててデータ量を削減する仕組みです。DQTと同じく1セグメント内に複数のテーブルが存在します。
このテーブルでは指定されたビット数に対し何通りのハフマンコードが存在するかを示し、そこに対応するデータ長の値を保持します。この部分に関してはそのほかにも保持する情報があり、説明が長くなるので後述します。

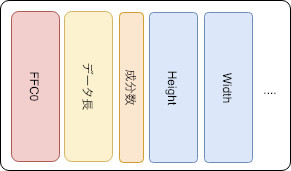
SOF

フレームヘッダー（Start Of Frame）
JPEG画像の縦横の大きさや描画方式など、基本的な情報についての情報が入っています。これについてはマーカが複数存在し、それによって描画方式や圧縮時の演算方式などを指定しています。
ffc0〜ffcfのうち、ffc4、ffc8、ffccの３つを除く13種類のマーカが存在し、一般にffc0、ffc2の2種類が使われています。描画方式や演算方式の違いについては今回は省略します。

SOS

スキャンヘッダー(Start Of Scan）
スキャンデータ、つまり実際に画像として描画されるのに利用されるデータの先頭にあるセグメントです。マーカはffdaです。圧縮方式についてなどの情報を保持しています。このセグメント以降に存在するデータを、各セグメントで得られた値を用いてデコードすることで、実際に描画で用いるrgb情報が得られます。

JPEGへの圧縮手順

各セグメントがどういった働きをしているのか（特にDQTやDHT）の動きを見るために、rgbデータをいかにしてjpgの形へ持っていくかをかいつまんで説明していきます。（興味がない人はこの項は読み飛ばしてください)

サンプリング

まず、元となるRGBデータの画像から、一辺8ピクセルの画像を抜き出します。これをMCU(Minimum Coded Unit)と呼び、圧縮処理における最小単位です。8ピクセルで抜き出せない場合、パディングと呼ばれるダミーのピクセルを用いて補完します。
このRGB情報から、輝度情報、色差情報（YCbCr)と呼ばれる情報に分解します。
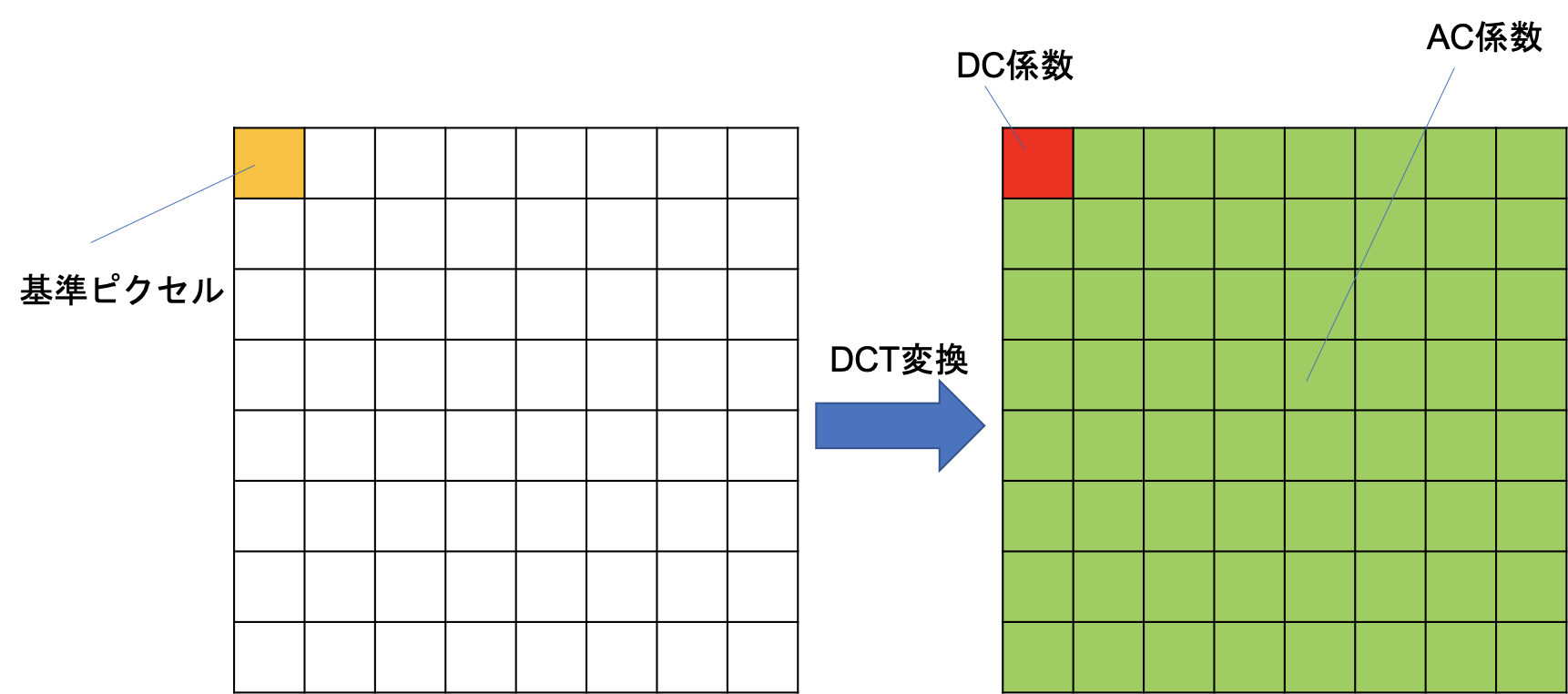
そうして得られた３つの8x8のピクセルブロックに、離散コサイン変換（DCT変換)と言う処理を行います。
この処理は、自分でもちゃんと理解していないのですが、一番左上のピクセルを基点とし、それ以外の部分を周波数の形でデータの変化を示したものです。この時、左上の基準部分に当たる部分を直列（DC)係数と呼び、その周囲の周波数に当たる部分をAC(並列）係数と呼びます。

量子化

この周波数変換を行ったMCUに対し、先程説明したDQTを用いて、６４個の係数で量子化します。
各係数を、量子化係数により割り、その商を記録することでデータ量を削減します。また周波数変換された値は、右下の値ほど、値を変えても元に戻した時に劣化が少ないと言う性質があるため、右下の値に対応する量子化係数ほど大きく、量子化された値を0にします。

zig-zag スキャン

量子化された係数は、左上から右下にかけてジグザグになるように並び替えられて記録されます。先の量子化で、右下に行くほど0の値が多くなるため、この方式で並び替えられた値は0の連なりが多くなり、後述するハフマン符号化で役立ちます。 ### ハフマン符号化 量子化されたMCUの係数を、DHTを用いてさらに圧縮していきます。ハフマン圧縮では、DC係数とAC係数でそれぞれ異なるテーブルを用い、それぞれのテーブルで保存される情報や、圧縮の方式も若干異なります。 DC係数の場合は係数をビット列にした上で、その長さの値と対応したハフマンコードをそのビット列の前にくっつけます。 AC係数の場合は、ハフマンテーブルがこのビットデータ長に加えて、ゼロがどれだけ続くかというランレングスの値を保持しており、何かしらの値の後に、複数個のゼロが連なっていた場合、その分をまとめて一つのハフマンコードで表せる形になります。あるポイントから、MCUの最後までずっとゼロが続いていた場合には、EOBと言う特殊なパターンを用いて、以降の表記を省略することもできます。

以上の形で作られたイメージデータをSOSヘッダの後に繋げて、末尾にEOIマーカをつけることでJPEGファイルが完成します。また、SOSには、輝度のMCUや、色差のMCUそれぞれに、どのDHTテーブルを用いるかが記され、SOFにはどのMCUにどのDQTテーブルを用いるかが示されていたりします。

JPEGファイルの中身をちょっと覗いてみる

さて、本題に戻って、実際にJPEGファイルをバイナリで読んで、SOF内の縦横サイズとDQTテーブルを表示してみましょう。（DHTテーブルについては、構造について説明していない部分があり、それだけでかなりの時間を取られるため今回は省略します)
言語はC++、PCはMacBook ProでOSは10.14.1で動作確認を行なっています。
まず、データ取得をするにあたり、それぞれのセグメントの構造を把握しておきます。

DQTセグメント構造

オフセット	名称	サイズ(バイト)	概要
0-1	マーカ	2	DQTセグメントを示すマーカ
2-3	データ長	2	セグメントのサイズを示す
4	量子テーブル精度	0.5(上位4bit)	量子テーブルの係数を何バイトで表すか　(0=1byte, 1=2byte)
4	量子テーブル番号	0.5(下位4bit)	量子テーブルの番号(０〜３)。SOFによりどのMCUに紐づくかがSOFで指定される
5-68	量子テーブル係数	それぞれ1	６４個の量子テーブル係数
...			以降、テーブル数の分続く

SOFテーブル構造

オフセット	名称	サイズ(バイト)	概要
0-1	マーカ	2	SOFセグメントを示すマーカ
2-3	データ長	2	セグメントのサイズを示す
4	成分数	1	サンプリング時に利用する値。今回は説明を省略
5-6	Height	2	画像の高さの値（px)
7-8	Width	2	画像の幅の値(px)
...			MCUとDHTの対応などが記述される。今回は説明を省略

実装

※質についてはご了承ください

#include <iostream>
#include <fstream>
#include <string>
#include <vector>

#define BYTE unsigned char
#define VECTARR(TYPE) vector< vector<TYPE> >

using namespace std;

// 指定した文字列をバイト列として比較する関数
bool cmp_bin(BYTE vect, string bin) {
  return (int)vect == strtol(bin.c_str(), NULL, 16);
}

// 指定した文字列に対応したバイト列を検索する関数
int search_vct(vector<BYTE> vect, string query) {
  if (query.size() > 2) {
    string first_q = query.substr(0, 2);
    string second_q = query.substr(2);

    for (int i = 0; i < vect.size() - 1; ++i) {
      if (cmp_bin(vect[i], first_q) && cmp_bin(vect[i + 1], second_q)) {
        return i;
      }
    }
    return -1;
  }
  for (int i = 0; i < vect.size(); ++i) {
    if ((char*)&vect[i] == query) {
      return i;
    }
  }
  return -1;
}

// 指定したセグメントの取得
VECTARR(BYTE) get_segments(vector<BYTE> vect, string name) {
  int index;
  VECTARR(BYTE) arr;
  while ((index = search_vct(vect, name)) > -1) {
    vector<BYTE> segment;
    // セグメントのサイズ取得
    int len = (vect[index + 2] << 8) + vect[index + 3] + 2;
    for (int i = index + 2; i < index + len; ++i) {
      segment.push_back(vect[i]);
    }
    arr.push_back(segment);
    vect.erase(vect.begin() + index, vect.begin() + index + len);
  }
  return arr;
}

int main(int argc, char* argv[]) {
    const char *filepath = argv[1];
    vector<BYTE> img_raw;

    // check argument
    if (argc < 2) {
        cout << "no filepath." << endl;
    }

    // 引数で指定したファイルのバイナリを取得
    ifstream ifs(filepath, ios::in | ios::binary);
    if (!ifs) {
        cout << "File open error." << endl;
        exit(-1);
    }
    img_raw.resize(ifs.seekg(0, ios::end).tellg());
    ifs.seekg(0, ios::beg).read((char*)&img_raw[0], img_raw.size());
    ifs.close();

    // SOIマーカを検索
    int soi_index = search_vct(img_raw, "ffd8");
    if (soi_index > -1) {
        cout << "This file is JPG file.\n" << endl;
    }
    else {
        cout << "This file is not JPG file.\n" << endl;
        exit(-1);
    }

    // DQT
    VECTARR(BYTE) ffdb = get_segments(img_raw, "ffdb");
    // SOF
    VECTARR(BYTE) ffcx_sof = get_segments(img_raw, "ffc0");

    // DQTテーブルの表示
    for (int i = 0; i < ffdb.size(); ++i) {
        vector<BYTE> dqt = ffdb[i];
        int len = (dqt[0] << 8) + dqt[1] - 2;
        dqt.erase(dqt.begin(), dqt.begin() + 2);
        for (int j = 0; j < len / 65; ++j) {
            int dqt_code = dqt[0] & 0x0f;
            cout << "量子化テーブル番号: " << dqt_code << endl;
            for (int k = 1; k < 65; ++k) {
                cout << +dqt[k] << ", " << flush;
                if (k % 8 == 0) {
                    cout << endl;
                }
            }
            cout << endl;
            dqt.erase(dqt.begin(), dqt.begin() + 65);
        }
    }

    // ffc0以外のSOFセグメントの場合そのまま終了
    if (ffcx_sof.size() == 0) {
        cout << "対応していないSOFセグメントです" << endl;
        exit(0);
    }

    int height = (ffcx_sof[0][3] << 8) + ffcx_sof[0][4];
    int width = (ffcx_sof[0][5] << 8) + ffcx_sof[0][6];

    cout << "Width: " << width << "px Height: " << height << "px" << endl;
    return 0;
}

結果

利用したファイル：profile.jpg

$ ./a.out profile.jpg
This file is JPG file.

量子化テーブル番号: 0
5, 3, 4, 4, 4, 3, 5, 4,
4, 4, 5, 5, 5, 6, 7, 12,
8, 7, 7, 7, 7, 15, 11, 11,
9, 12, 17, 15, 18, 18, 17, 15,
17, 17, 19, 22, 28, 23, 19, 20,
26, 21, 17, 17, 24, 33, 24, 26,
29, 29, 31, 31, 31, 19, 23, 34,
36, 34, 30, 36, 28, 30, 31, 30,

量子化テーブル番号: 1
5, 5, 5, 7, 6, 7, 14, 8,
8, 14, 30, 20, 17, 20, 30, 30,
30, 30, 30, 30, 30, 30, 30, 30,
30, 30, 30, 30, 30, 30, 30, 30,
30, 30, 30, 30, 30, 30, 30, 30,
30, 30, 30, 30, 30, 30, 30, 30,
30, 30, 30, 30, 30, 30, 30, 30,
30, 30, 30, 30, 30, 30, 30, 30,

Width: 25px Height: 25px

無事、量子テーブルと縦横サイズが取得できました

最後に

いかがでしたか？
JPEG画像一つを見ても、色々な工夫を凝らしてサイズを削減していると言うことが、少しでも伝わっていれば幸いです。
バイナリの扱いについては経験が少なく、structを使うなどもっといいやり方もあると思うので、上記の知識をつけた上で個人で取り組んでみるのもありだと思います。
学生時代に、MCUを取り出して係数の一部を操作し、電子透かしを埋め込むといったコードを書いたことがあるので、気が向いたら見せられるレベルに整形して置いてみるかもしれません。

皆さんもJPEGをバラして遊んでみましょう。
それでは、どうもありがとうございました。

参考資料

• JPEG file format hack (http://uno036.starfree.jp/PRGmanual/ImageFormatJpg4/index.html )
• JpegAnalyzer Plus　オンラインヘルプ (http://hp.vector.co.jp/authors/VA032610/ )
• JPGファイルフォーマット (https://www.setsuki.com/hsp/ext/jpg.htm )