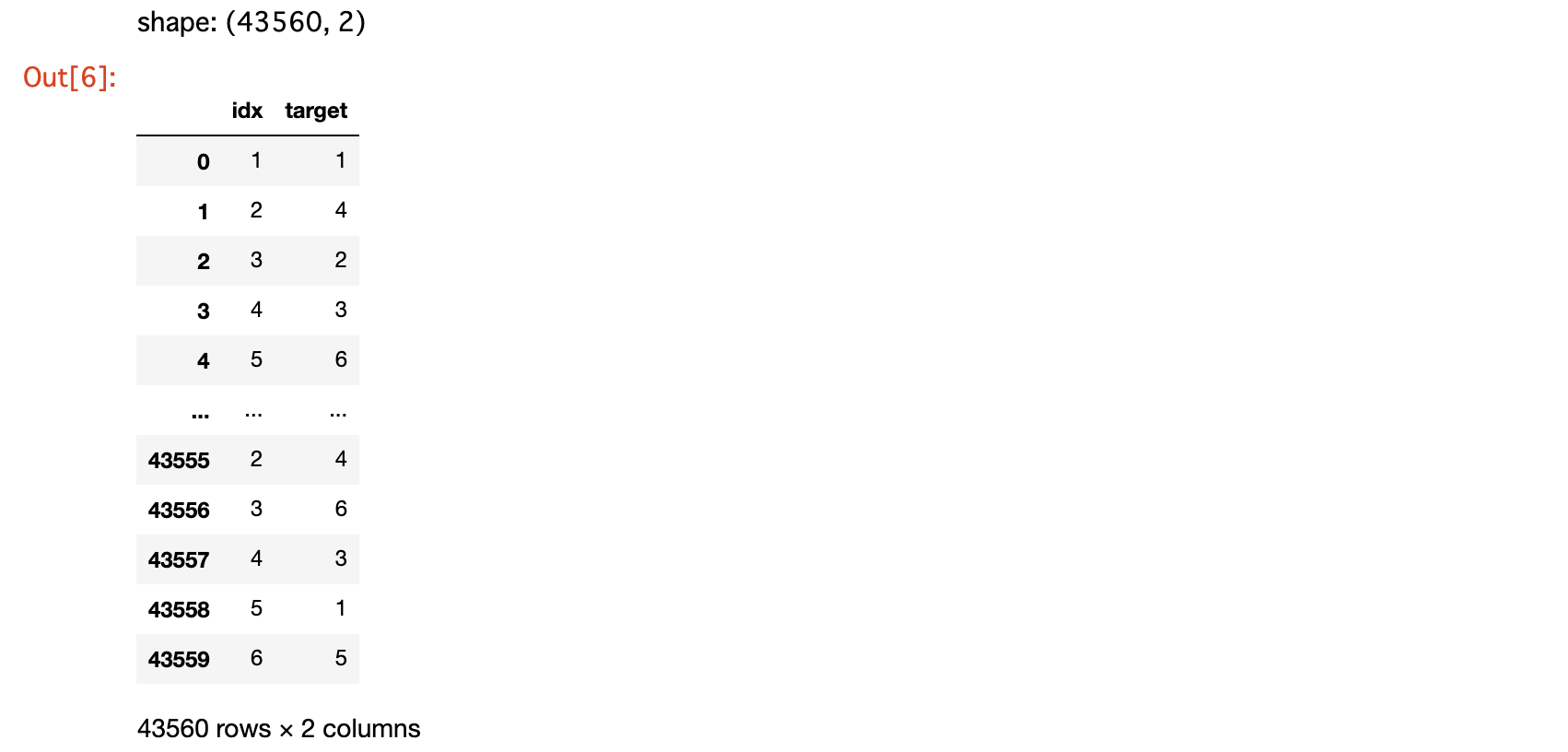はじめに
競艇のルール,予想の仕方など私自身何もその辺の知識がないことをご了承ください.
それらすべてをデータ分析,機械学習に任せることによって知識のない人間でも利益をプラスにできるのではないか,そういう魂胆でこの記事を書いています.
環境
MacOS BigSur 11.4
Jupyter Notebook(Colaboratoryでも可)
データについて
競艇公式ホームページ BOAT RACEからスクレイピングによってデータを取得しました.
会場:住之江会場
データ数:43560件
期間:2019/01 ~ 2020/04
今回の目的
競艇はスタート位置でほぼ決まる.みたいな話を聞いたことがあります.
データ分析によってこれが本当なのかを調べるのが今回の目標です.
本編
ライブラリのimport
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from itertools import product
前処理
データはsuminoe_40000_program.csvとsuminoe_40000_answer.csvに格納されているため,PandasによってDataFrame形式でデータを読み込みます.
説明変数
names = ["Place", "Number", "Name", "Age", "Live",
"Weight", "Rank", "A_1st", "A_2nd", "B_1st",
"B_2nd", "Moter_No", "Moter_2nd", "Bote_No", "Bote_2nd"]
df_program = pd.read_csv("../../Boat-Race-Prediction/suminoe_40000_program.csv", names=names)
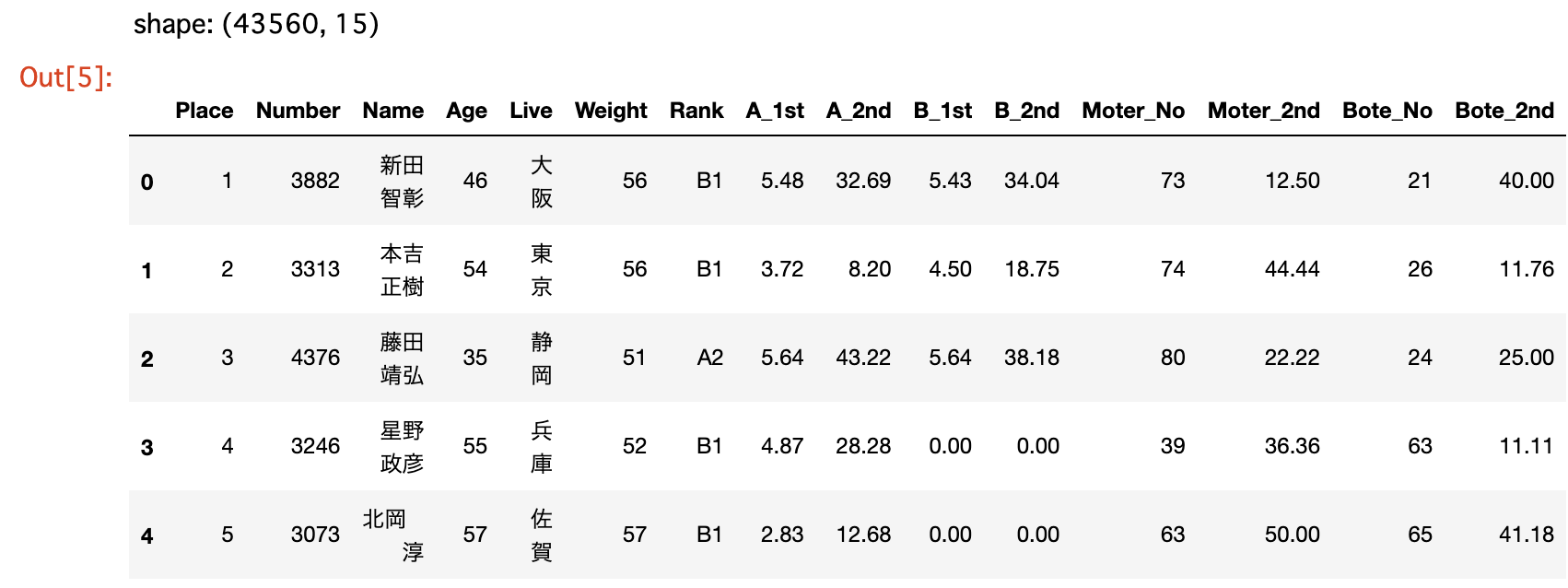
print(f"shape: {df_program.shape}")
df_program.head()
目的変数
df_answer = pd.read_csv("../../Boat-Race-Prediction/suminoe_40000_answer.csv", names=["idx", "target"])
print(f"shape: {df_answer.shape}")
df_answer
OneHotEncoding
説明変数を見ると,Name, Live, Rankはカテゴリ変数となっていることがわかります.
名前Nameと地域LiveについてはOneHotEncodingしてしまうと ,列数がとんでもないことになってしまうため今回はデータから弾くことにします.
よってRankをOneHorEncodingによって,A1, A2, B1, B2の列を新たに作成します.
(目的変数のidxも必要ないため弾いています.)
df_data = df_program.merge(df_answer, how="inner", right_index=True, left_index=True)
df_data = df_data.drop(["idx", "Name", "Live"], axis=1)
df_dummies = pd.get_dummies(df_data, columns=["Rank"])
df_dummies.head()
目的変数の前処理
競艇には転覆やスタートミスによって失格判定になる場合があります.
生データではtargetの部分がK, Fのようなカテゴリ変数となっています.
できるだけ数値のみのデータとして扱いため,10, 11, 12の値に変換してあります.
今回の分析でこれらのデータは使用しないため,np.nanによって欠損値扱いとします.
df_dummies.target[df_dummies.target == 10] = np.nan
df_dummies.target[df_dummies.target == 11] = np.nan
df_dummies.target[df_dummies.target == 12] = np.nan
各列とtargetの相関を見る
targetと各変数の関係を相関係数を計算することによって調べます.
わかりやすさのために,Seaboanのヒートマップを使用しています.
# 相関係数を表示
plt.rcParams['figure.figsize'] = (20.0, 10.0)
plt.rcParams['font.family'] = 'serif'
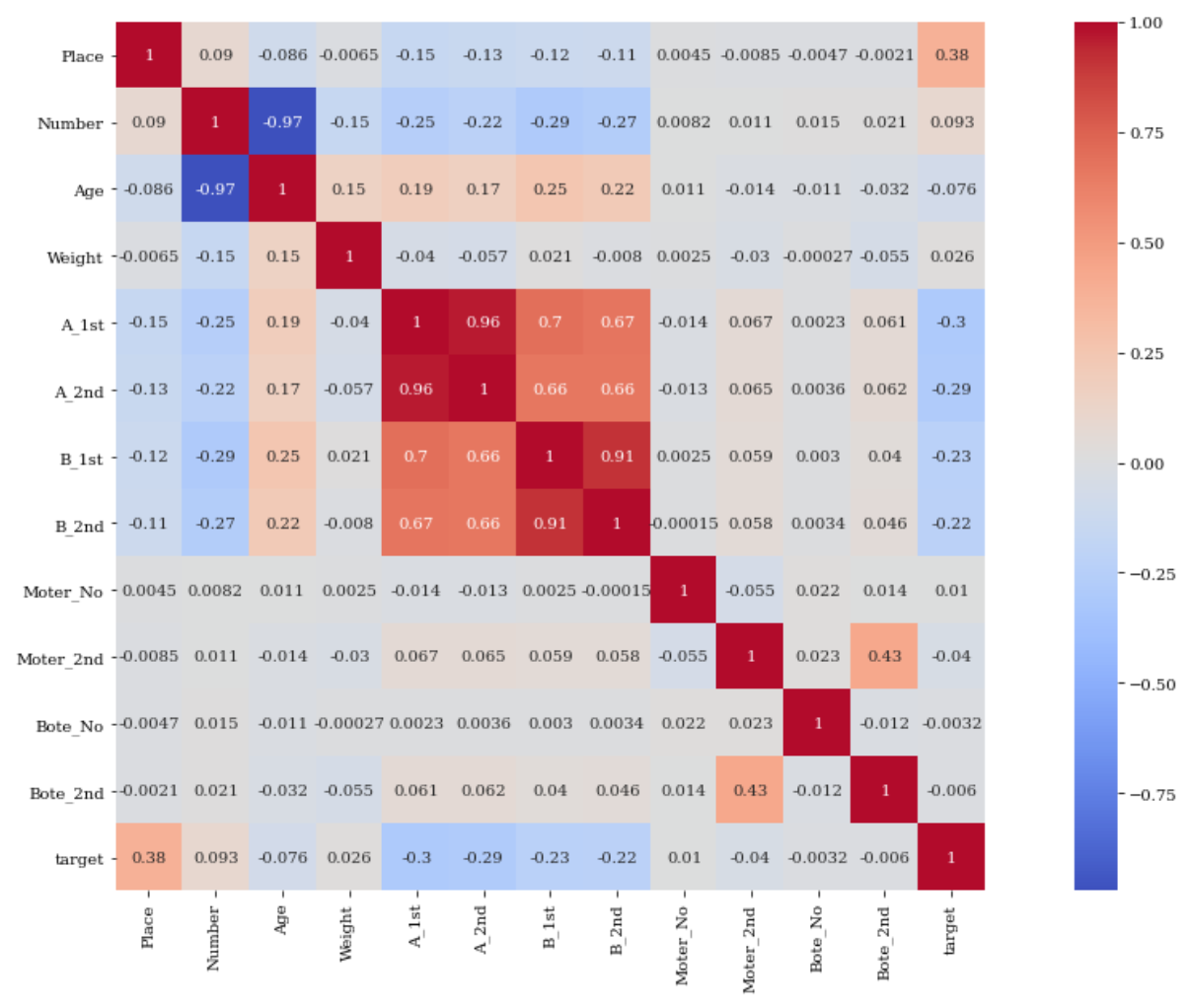
sns.heatmap(df_data.corr(), annot=True, square=True, cmap='coolwarm');
このヒートマップから,targetとPlaceの間には,0.38の正の相関があることがわかります.
0.38という値は強い相関とは言えませんが,やや相関があると言えます.
なので,targetとPlaceをヒストグラムで示してみましょう.
targetとPlaceの関係をヒストグラムで可視化する
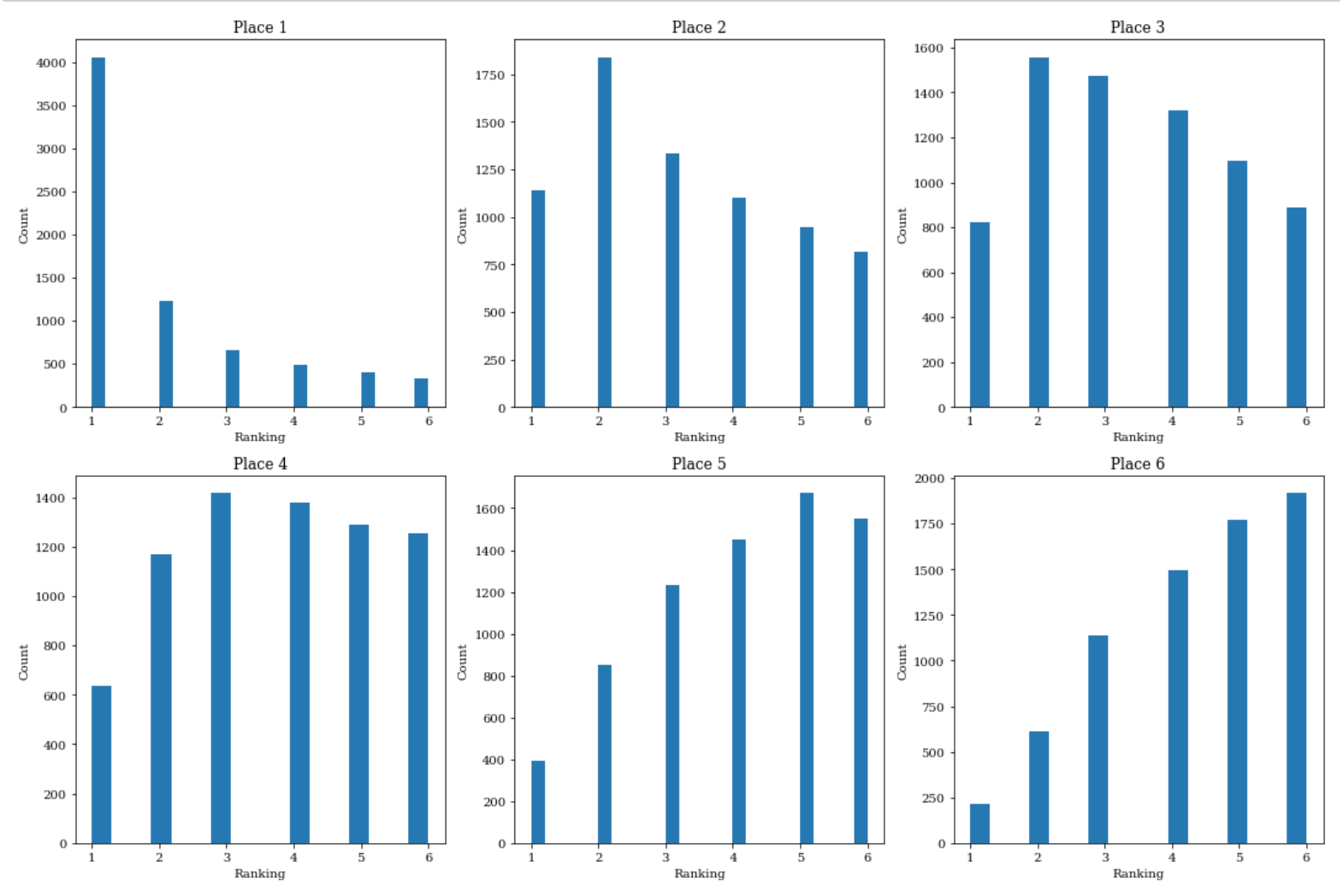
各スタート位置に対する順位をヒストグラムによって可視化してみます.
これによって位置がどのくらい順位に影響するのかがわかるはずです.
fig, ax = plt.subplots(2, 3, figsize=(15, 10))
for i, tu in zip(range(1, 7), product(range(2), range(3))):
df_place = df_dummies[df_dummies.Place == i]
ax[tu[0], tu[1]].hist(df_place.target, bins='auto')
ax[tu[0], tu[1]].title.set_text(f'Place {i}')
ax[tu[0], tu[1]].set_xlabel('Ranking')
ax[tu[0], tu[1]].set_ylabel('Count')
plt.tight_layout()
スタート位置が1である場合に1位になる確率はとてつもなく高そうです.
スタート位置が6に近づくにつれて1位になる確率は下がっていっていることがわかります.
では,位置に対する順位の確率を算出してみましょう.
for i in range(1, 7):
df_place = df_dummies[df_dummies.Place == i]
print(f"Place: {i}")
for j in range(1, 7):
df_target = df_place[df_place.target == j]
probability = df_target.shape[0] / df_place.shape[0] * 100
print("\t{}: {:.1f}%".format(j, probability))
Place: 1
1: 55.9%
2: 16.9%
3: 9.1%
4: 6.8%
5: 5.5%
6: 4.6%
Place: 2
1: 15.7%
2: 25.4%
3: 18.3%
4: 15.1%
5: 13.0%
6: 11.3%
Place: 3
1: 11.3%
2: 21.5%
3: 20.3%
4: 18.2%
5: 15.1%
6: 12.2%
Place: 4
1: 8.7%
2: 16.1%
3: 19.5%
4: 19.0%
5: 17.8%
6: 17.3%
Place: 5
1: 5.4%
2: 11.7%
3: 17.0%
4: 20.0%
5: 23.0%
6: 21.4%
Place: 6
1: 3.0%
2: 8.4%
3: 15.7%
4: 20.6%
5: 24.4%
6: 26.4%
スタート位置が1であったときに1位になる確率は,55.9%であることがわかりました!
よって,1レース6人であるため,データでは1レース6行で表現されます.なので,今回のデータは43560件であるため,
43560 / 6 = 7260レース分のデータが存在しています.
この7260レース中のうち,55.9%が1位になるため,スタート位置が1である選手は7360中4058回1位になっていることが今回のデータからわかりました.
まとめ
絶対というわけではないですが,スタート位置だけでも順位にそれなりに影響するようです.
しかしスタート位置が2, 3, 4の場合は順位にあまり差がないため,3連単などを当てるためには他の点で分析していく必要があると思います.
ここまでのデータ分析で使えるのは単勝予想くらいだと思います.