jComprehensionの紹介

この記事はSRA Advent Calendar 2016の3日目の記事です。

※この記事は関ジャバでの「JavaOne 2016 報告会 in 大阪」で発表した資料にコメントを付け加えたものです。

---

JavaOne2016のセッションの中で「List Comprehensions in Java 8」というセッションがありました。
そこで登場したjComprehensionというライブラリを紹介します。
（登場したというより、このライブラリを紹介するというセッションでした）

リストの内包表記

セッションのタイトルにもある「List Comprehension」とは「リストの内包表記」のことです。

集合の内包表記については後に解説したいと思います。

これは実際にJavaOneのセッションで使われた資料を登壇者がアップロードしたものの抜粋ですが、HaskellやPythonでのリストの内包表記の記述例を示し「じゃあJavaだとどうなるの？」という話です。
一番上の「Set-builder notaion」については後に解説いたします。

例えば「1～4までの偶数」というリストを作る場合、Javaだと

• forループを使う方法
• Stream APIとLambda式を使う方法

があります。
これを、jComprehensionを使うと

このように書けます。
個人的にはStream APIを使った書き方で十分わかりやすいと思いますが。。。

jComprehension API

jComprehensionはシンプルなライブラリで、以下の2つのクラスがあるだけです。

class ListComprehension<T>

  public List<T> suchThat(Consumer<Var> predicates)
  public List<Pair<T, T>> suchThat(BiConsumer<Var, Var> predicates)

  public ListComprehension<T> outputExpression(Function<T, T> resultTransformer)
  public ListComprehension<T> outputExpression(BiFunction<T, T, Pair<T, T>> resultTransformer)

class Var<T>

  public Var belongsTo(List<T> c)

  public Var is(Predicate<T> p)
  public Var is(BiPredicate<T, T> p)

  public Var holds(Predicate<T> p)
  public Var holds(BiPredicate<T, T> p)

Varクラスのisメソッドはholdsメソッドの単なるエイリアスですので、Varクラスのメソッドは実質３つです。

集合の有用性

jComprehensionは集合の概念をJavaに取り入れたライブラリと言えますが、普段業務アプリケーションなどを開発している人には関係ないのでしょうか？
私はそうは思いません。「集合」という考え方はありとあらゆるところにあるからです。
例えば、大学などのシステムの利用者（アクター）を考えてみると

• 学生
• 教師
• 職員

などがありますが、これらはそれぞれの条件を満たす人の集まり（＝集合）です。
また、良くあるシステムの「メニュー」ですが、「ログインしたユーザが使うことができる機能」の集合と言えます。
このように集合は身近にあり、システム開発で（無意識であっても）よく使われる概念です。

集合の内包表記（Set-builder notaion）

集合の有用性がわかったところで、後に解説するといった「集合の内包表記」と「Set-builder notaion」ですが、実はこの2つは同じようなものと考えられます。
集合とその表記法について確認しておきましょう。
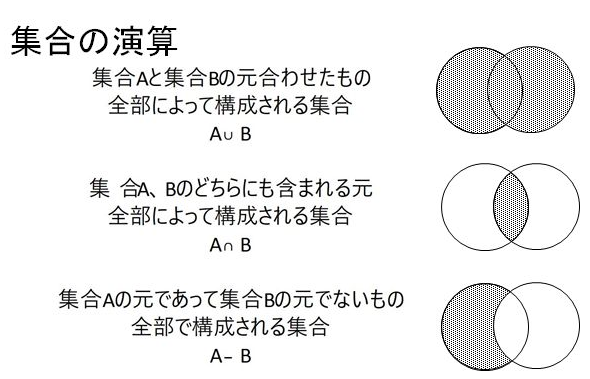
集合

一定の条件に適し、他のものと明確に区別できるものの全体を「集合」という
また、集合に属している個々のものを、その集合の「元（要素）」という

集合の外延的表記

集合の元を列挙する記述法を集合の外延的表記という
{1, 2, 3, 4, 5}

集合の内包的表記

任意の元 x を示し、xの満たす条件を添える記述法を内包的表記という
{ x | 1 ≦ x ≦ 5, xは整数 }

集合の基本

次に、集合の基本事項についてです。

実数とは

上記でRは慣例的に実数の集合と述べましたが、有理数が「2つの整数a, b(a>0)に対して b/a で表される数の集合」と定義されているのに対し、実数は「実数の集合」とだけ書かれています。
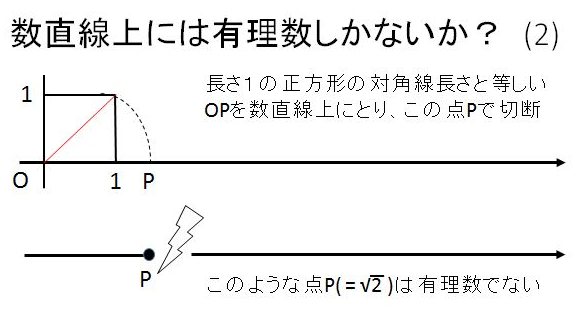
実は実数を定義するのは簡単ではなく、ここでは有理数に無理数を完備して定義する方法を見てみましょう。

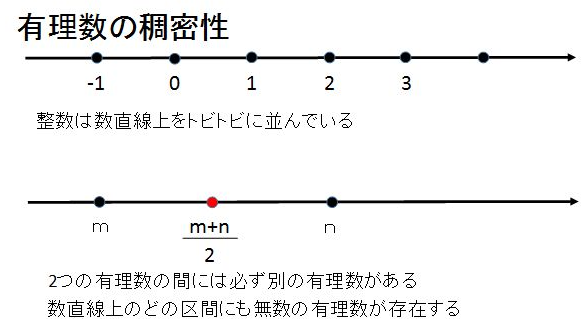
数直線のどの範囲を調べても、そこには無数の有理数が存在します。
有理数と有理数の間には必ず別の有理数があるのですから、繰り返していけばいくらでも有理数を見つけることができますね。
数直線上のどの範囲にも有理数が無数にあるということは、数直線は有理数が隙間なく詰まっているのではと考えられます。
実際にはそうではないのですが、まずは数直線を2つに切ることから考えてみましょう。

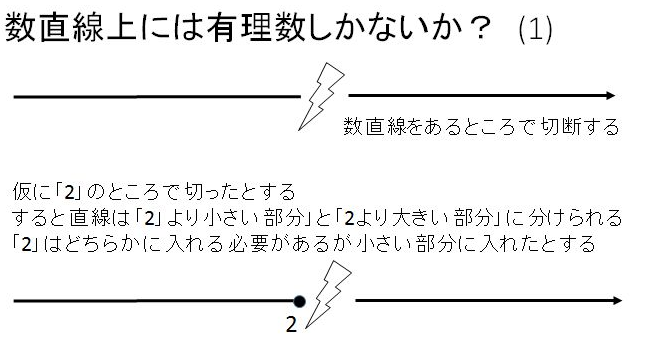
この切断では切断した左（小さいほう）の端っこが「2」という有理数です。

この切断では端っこが有理数ではありません。

このように有理数の集合を一方が他方の全ての元より小であるような二組にわけることをデデキントの切断といいます。

デデキントの切断を使い、有理数の隙間を埋める（完備する）形で実数を定義することを実数の連続性（完備性）といいます。

集合の濃度

次に集合の要素の「多さ」について考えてみます。
例えば、「１から１０の偶数」の場合、要素の数は{2, 4, 6, 8, 10}の「５」となります。
また、「１から１０までの素数」となると要素数は{2, 3, 5, 7}「４」となり、偶数よりも少ないことがわかります。

有限集合の場合はこのように「要素の数」を比べることによって「多さ」を比較することができます。
では無限集合の場合はどうでしょうか。
例えば、「正の偶数」と「自然数」で考えてみます。
自然数は正の偶数の要素とさらに奇数の要素を持っているので自然数のほうが多そうです。

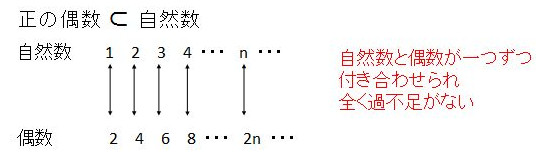
ところがこのように「自然数 n」に対して偶数は2nと付き合わせるとどちらも余ることがありません。
なので「正の偶数」と「自然数」は同じ「多さ」と言えます。

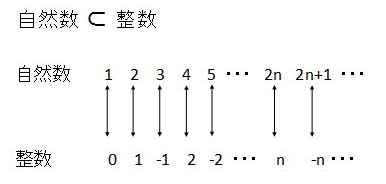
同様に自然数にゼロと負の数が要素に加わった「整数」の場合も自然数と同じ「多さ」となります。
これらの例のように２つの集合A,Bがあり、AからBへの一対一の対応が少なくとも一つあるとき、「AはBと対等である」といい
　A～B
と書きます。
また、無限集合も含めた集合の要素の「多さ」を濃度といい、集合Aの濃度を
　|A|
と書きます。
そしてN（自然数）やZ（整数）のように「要素を順番に並べることができる」無限集合のことを可算集合や可付番集合と言い、その濃度を

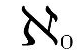
と書いて「アレフ・ゼロ」と言います。
先ほどの
N～Z（自然数と整数は対等）
ということを知ると「じゃあ無限集合は全て同じ濃度なの？」と思ったりもしますが、実はR（実数）は可算集合ではなく、

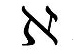
と書き「アレフ」という濃度であることが知られています。
つまり、RはNやZよりも要素が多いということです。
さらに、「アレフ・ゼロ」と「アレフ」の中間の濃度は存在しないというのが連続体仮説と言われるものです。

JavaOne2016 Keynote

ここまでの話を聞いて「Javaに関係ない話がずっと続いている」と感じた方はラッキーです。
なぜならJavaOne2016のKeynoteでは「火星探査の話」が一時間ほど続き、会場にいた人たちは「延々とJavaに関係ない話が続いているんだが・・・」という気持ちでした。
なので皆さんはサンフランシスコまで行くことなく、JavaOne参加者と同じ気分が味わえました。

・・・と「JavaOne2016 報告会 in 大阪」ではこのような話をしました。
正直、このオチを楽しんでもらえるかどうか不安でしたが、聞いていただいた方々は皆さん温かく、ドッカンとウケました。
おかげでその後も気持ちよく話ができて、最後の「会場付近のバー紹介」も楽しくできました。

ちなみに発表に使った資料の完全版はここに置いています。