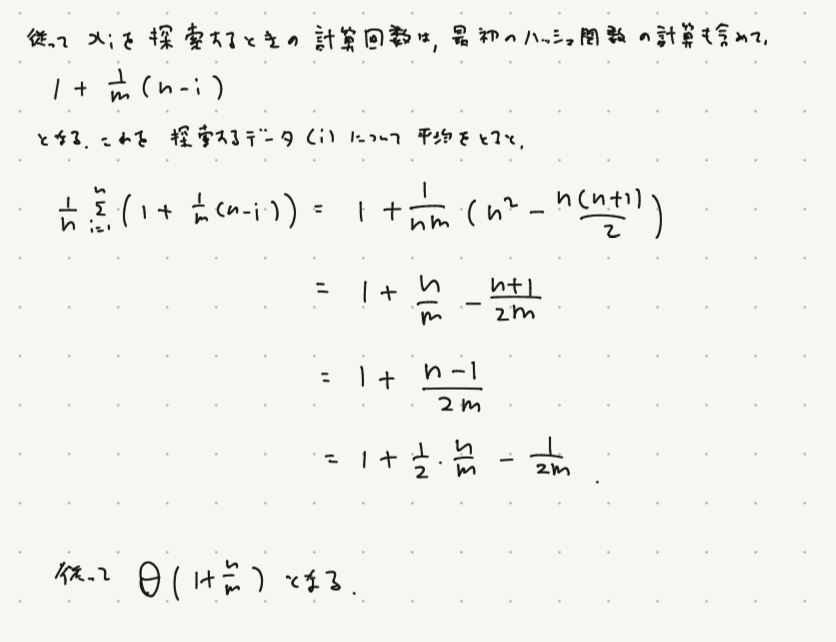1.はじめに
友人と応用情報の勉強会を始めたのでそれ用のまとめです.
各個人が気になったところ,もう少し知りたいなと思ったところを勝手にまとめて共有する方式の勉強会です.(毎回記事にするかは怪しい)
記事としては既出もいいところでしょうが,今回の僕のテーマは探索アルゴリズム(ハッシュ探索)です.
(綺麗にまとまっていませんが後日時間があれば追記したり整理します...)
アルゴリズムについて
まず僕がこれをテーマに選んだのは,今までハッシュは全単射じゃないと意味がない(完全に全単射は無理でしょうが,それに近いもの)と思っていたのですが,このハッシュ探索では,全単射が理想ではあるものの,そうでなくとも探索対象の集合を分割できるだけでも意味があるんだ,というもので賢いなと感動したからです.
ハッシュはあくまでも道具であって,目的(解きたい問題)によっては使い方も変わるんだなと.
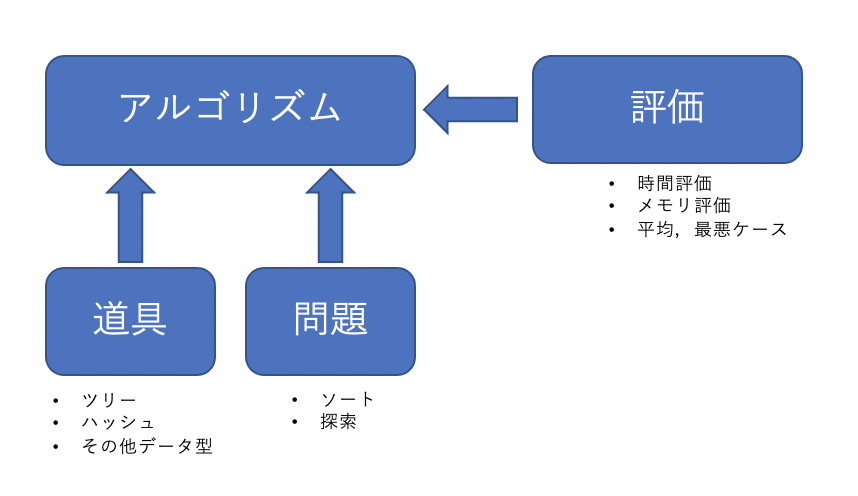
図にするとこんな感じで,冷静になると当たり前と言えば当たり前なのですが,アルゴリズムについてはこんな感じのイメージを持っておくのが良さそうだなと思いました.
2.ハッシュ探索について
ongoing
3.ハッシュ探索の実装(チェイン法)
class HashTable(object):
def __init__(self, m: int):
self.m = m
hash_table = {}
for key in self._hash_val_set:
hash_table[key] = []
self.hash_table = hash_table
def _hash_func(self, key):
hash_val = key % self.m
return hash_val
@property
def _hash_val_set(self):
return set(range(self.m))
def insert(self, a: int):
self.hash_table[self._hash_func(a)].append(a)
def delete(self, a: int):
self.hash_table[self._hash_func(a)].remove(a)
def search(self, a: int) -> bool:
for elem in self.hash_table[self._hash_func(a)]:
if elem == a:
return True
return False
def __str__(self):
output_str = ""
for key, val in self.hash_table.items():
output_str += f"{key}: {val}\n"
return output_str
4.計算量
計算したい$x_{i}$がハッシュテーブルの中に入っていないとき,リストの最後まで探索することになる.
このとき,各リストの長さはハッシュが単純一様ならば$n/m$の長さなので,ハッシュ関数の計算も含めて$1+n/m$.
計算したい$x_{i}$がハッシュテーブルの中に入っているとき,以下のようになって,$1+n/m$.
(走り書きです...後日時間があれば綺麗にします)
つまりどちらの場合も$O(n/m)$となる.
ちなみに本ではO(1+n/m)と書いていて、何故1+を明示的に書いているのだろうと思ったが、多分mを大きくしてn/mはゼロに近くできるという話をしたいので、1+がないとオーダーゼロです!みたいな話になってしまうからだろう。オーダーゼロはありえないので(計算しようと思った時にはすでに終わってるみたいなことになってしまう)
5.時間を測ってみる
さてオーダーが$n/m$なので,実際に1つずつ変化させて時間を測ってみたらnを増やしたら線形に増える,mを増やしたら反比例して減るはずである.確かめてみる.
import timeit
from random import randint
import pandas as pd
class Simulater(object):
def __init__(self):
self.max_int = 1000000
self.sim_iter_num = 100000
def _simulate(self, m, a_list):
hashtable = HashTable(m=m)
for a in a_list:
hashtable.insert(a)
result_time = timeit.timeit(lambda: hashtable.search(randint(0, self.max_int)), number=self.sim_iter_num)
result_time_mean = result_time / self.sim_iter_num
return result_time_mean
def simulate_on_m(self, m_list: list, a_list: list) -> pd.DataFrame:
result_time_mean_list = []
for m in m_list:
result_time_mean = self._simulate(m, a_list)
result_time_mean_list.append(result_time_mean)
result_df = pd.DataFrame({"m": m_list, "time": result_time_mean_list})
return result_df
def simulate_on_a_list_len(self, a_list_len_list: list, m: int) -> pd.DataFrame:
result_time_mean_list = []
for a_list_len in a_list_len_list:
a_list = [randint(0, self.max_int) for _ in range(0, a_list_len)]
result_time_mean = self._simulate(m, a_list)
result_time_mean_list.append(result_time_mean)
result_df = pd.DataFrame({"a_list_len": a_list_len_list, "time": result_time_mean_list})
return result_df
a_list = [randint(0, 1000000) for _ in range(0, 10000)]
result_df_on_m = Simulater().simulate_on_m(range(1, 50, 3), a_list)
result_df_on_a_list_len = Simulater().simulate_on_a_list_len(range(1, 10000, 1000), m=7)
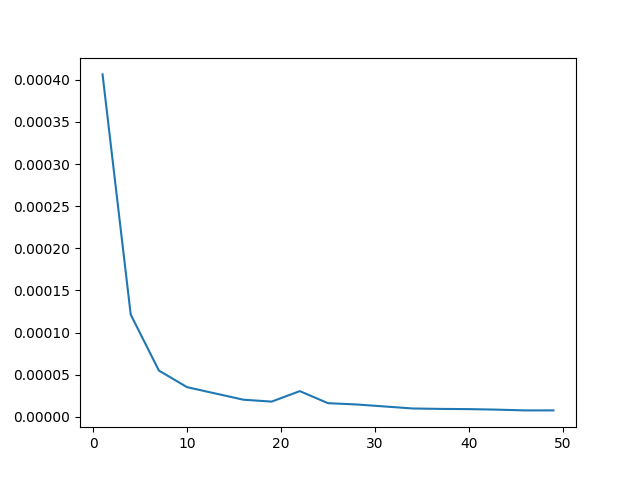
mを動かした時
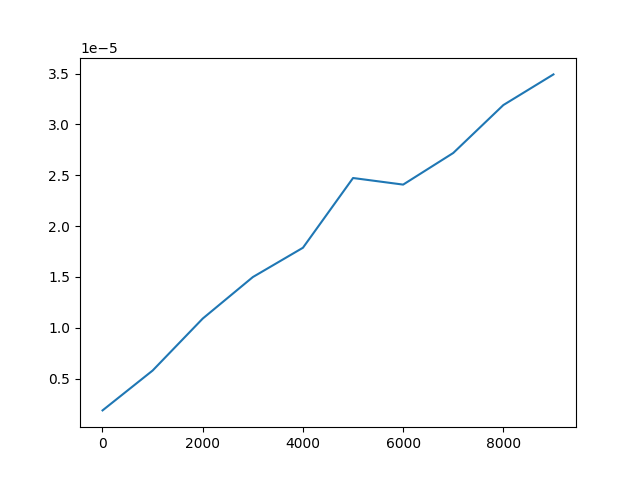
nを動かした時
だいたいそうなってる.
6. 参考文献
- MIT教科書 アルゴリズムイントロダクション
- 平田富夫 アルゴリズムと設計とデータ構造