多変量t分布の導出とpythonによる乱数生成の実装

はじめに

多変量t分布について調べていたので，そのまとめです．

（この記事を書き上げた瞬間，データを吹っ飛ばして書き直しました...死にたい...）

多変量t分布の導出

定義

ググって一番最初にみつかるという理由から，wikipediaのMultivariate t-distributionのノーテーションにに従います．
多変量t分布の確率密度関数は，以下で定義されます．

$$
p(\textbf{x}) = \frac{\Gamma\Bigl[{\frac{\nu+p}{2}}\Bigr]}{\Gamma\Bigl[{\frac{\nu}{2}}\Bigr] \nu^{\frac{p}{2}}\pi^{\frac{p}{2}} \det(\Sigma)^{\frac{1}{2}}} \Bigl[ 1 + \frac{1}{\nu} (\textbf{x} - {\bf \mu})^{T} {\bf \Sigma}^{-1}(\textbf{x} - {\bf \mu})\bigr]^{\frac{-(\nu+p)}{2}}. \tag{1}
$$

理論

ポイント

そもそもt分布とはなんぞやという話になりますが，t分布とは，正規分布の分散を増減させるパラメーターを考え，それにガンマ分布を仮定し，結局は積分消去したもの，と言えます．
ここで，ガンマ分布ではなく逆ガンマ分布，カイ2乗分布を仮定することもありますが，少しの変更で全て同値になりそうです．（試してない）

これによって，分散の値がよくわからないときに，その平均的な振る舞いを見ることができます．

導出

二つの確率変数 $V \sim Gam(\alpha, \beta)$，$X \sim N(\textbf{0}, {\bf \Sigma})$ を考えます．$X$は$d$次元正規分布とします．
この二つの確率変数を，関数 $f,g$ によって，$Y,U$に変換します．
$$
Y = f(V,X) = \mu + \frac{1}{\sqrt{V}}X, \tag{2}
$$
$$
U = g(V,X) = g(V)= V. \tag{3}
$$

ここで，$g$は$V$の恒等関数であり，$\mu \in \mathbb{ R }^{d}$は平均を表すd次元ベクトル，$V$は$X$と独立と仮定します．

この$f(\cdot)$は，$V$を固定すると直線（平面）の関数であり，1対1対応の関数です．従って，逆関数$f^{-1}(\cdot)$が存在し，
$$
f^{-1}(Y) = X = \sqrt{U}(Y - \mu), \tag{4}
$$
となります．

すでに分布の分かっている$V,X$から，$Y$の分布を求めます．確率変数は$U$と$Y$の2つあるので，$U,Y$の同時分布を考えて，$U$について積分消去することで$Y$の分布を求めます．

Pr(u,y) = Pr(U < u, Y < y) = Pr(g(V) < u,f(X) < y) \\
= Pr(V < g^{-1}(u), X < f^{-1}(y)) \\
= Pr(V < u, X<\sqrt{u}(y - \mu)) = Pr(V < u) Pr(X < \sqrt{u}(y - \mu)). \tag{5}

ここで，$V$と$X$は独立の仮定，
$$
Pr(v,x) = Pr(v)Pr(x), \tag{6}
$$
を使いました．

$p_{V},p_{X}$をそれぞれ$V$と$X$の確率密度関数とすると，
$$
Pr(u,y) = Pr(V < u) Pr(X < \sqrt{u}(y - \mu)) = \int_{-\infty}^{u} \int_{-\infty}^{y} p_{V}(u)p_{X} (\sqrt{u}(y - \mu)) |\det(J)| dudy. \tag{7}
$$

ここで，$|\det(J)|$は変数変換によって生じたヤコビアンであり，ヤコビ行列$J$ （$(d+1)*(d+1)$行列）は，

J = \begin{pmatrix} \frac{\partial x}{\partial y^{T}} & \frac{\partial x}{\partial u} \\ \frac{\partial v}{\partial y^{T}} & \frac{\partial v}{\partial u} \end{pmatrix} =
 \begin{pmatrix} \sqrt{u}I_{d} & \frac{1}{2\sqrt{u}(y-\mu)} \\ \textbf{0} & 1 \end{pmatrix}. \tag{8}

ヤコビ行列$J$が上三角行列なので，その行列式は対角要素の積となり，
$$
\det(J) = u^{\frac{d}{2}}. \tag{9}
$$
　　
$(7)$の積分の中身は，$Pr(u,y)$の確率密度関数$p_{U,Y}(u,y)$であるため，これを求めます．
$V \sim Gam(\alpha, \beta)$，$X \sim N(\textbf{0}, {\bf \Sigma})$より，
$$
p_{V}(v) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} v^{\alpha-1} \exp{( - \beta v)}, \tag{10}
$$
$$
p_{X}(\textbf{x}) = \frac{1}{(2\pi)^{\frac{d}{2}}} \frac{1}{\sqrt{\det(\Sigma)}} \exp{\Bigl( - \frac{1}{2} \textbf{x}^{T} \Sigma^{-1} \textbf{x} \Bigr)}, \tag{11}
$$
従って，
$$
p_{V}(u) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} u^{\alpha-1} \exp{( - \beta u)} = Gam(\alpha, \beta), \tag{12}
$$

p_{X}(\sqrt{u}(\textbf{y} - \mu)) = \frac{1}{(2\pi)^{\frac{d}{2}}} \frac{1}{\sqrt{\det(\Sigma)}} \exp{\Bigl( - \frac{1}{2} \sqrt{u}(\textbf{y} - \mu)^{T} \Sigma^{-1} \sqrt{u}(\textbf{y} - \mu) \Bigr)} \\
= \frac{1}{(2\pi)^{\frac{d}{2}}} u^{-\frac{d}{2}} u^{\frac{d}{2}} \frac{1}{\sqrt{\det(\Sigma)}} \exp{\Bigl( - \frac{1}{2} (\textbf{y} - \mu)^{T} (u \Sigma^{-1}) (\textbf{y} - \mu) \Bigr)} \\
=  u^{-\frac{d}{2}} \frac{1}{(2\pi)^{\frac{d}{2}}}  \frac{1}{\sqrt{\det(\frac{\Sigma}{u})}} \exp{\Bigl( - \frac{1}{2} (\textbf{y} - \mu)^{T} (u \Sigma^{-1}) (\textbf{y} - \mu) \Bigr)} = u^{-\frac{d}{2}} N(\mu, \frac{\Sigma}{u}). \tag{13}

$Pr(u,y)$の確率密度関数$p_{U,Y}(u,y)$は，
$$
p_{U,Y}(u,y) = Gam(\alpha, \beta) u^{-\frac{d}{2}} N(\mu, \frac{\Sigma}{u}) |\det(J)| = Gam(\alpha, \beta) N(\mu, \frac{\Sigma}{u}) u^{-\frac{d}{2}}u^{\frac{d}{2}} = Gam(\alpha, \beta) N(\mu, \frac{\Sigma}{u}). \tag{14}
$$
（ここで，ガンマ分布の台は$u \in [0,\infty), d>0$より，絶対値は外してよい．）

$p_{U,Y}(u,y)$を$u$について積分することによって，$Y$の確率密度関数$p_{Y}$を得ます．
$$
p_{Y} = \int_{0}^{\infty} p_{U,Y}(u,y)du = \int_{0}^{\infty} Gam(\alpha, \beta) N(\mu, \frac{\Sigma}{u})du \tag{15}
$$

ここで，記法の簡略化のために，正規分布のマハラノビスの距離を，$\Delta^{2} = (\textbf{y} - \mu)^{T}\Sigma^{-1}(\textbf{y} - \mu)$と表記します．

$$
p_{Y}(\textbf{y}) = \int_{0}^{\infty} \frac{\beta^{\alpha}}{\Gamma(\alpha)} u^{\alpha-1} \exp{( - \beta u)} u^{-\frac{d}{2}} \frac{1}{(2\pi)^{\frac{d}{2}}} \frac{1}{\sqrt{\det(\frac{\Sigma}{u})}} \exp{\Bigl( - \frac{u}{2} \Delta^{2} \Bigr)} du. \tag{16}
$$
$u$に依存した部分のみを抜き出し，
$$
p_{Y}(\textbf{y}) \propto \int_{0}^{\infty} u^{\alpha-1} \exp{( - \beta u)} u^{\frac{d}{2}} \exp{\Bigl( - \frac{u}{2} \Delta^{2} \Bigr)} du \
= \int_{0}^{\infty} u^{\frac{d}{2}+\alpha-1} \exp{\Bigl( - u( \beta + \frac{\Delta^{2}}{2} ) \Bigr)} du. \tag{17}
$$

ここで，$z = u(\beta + \frac{\Delta^{2}}{2})$とおくと，$u = z(\beta + \frac{\Delta^{2}}{2})^{-1}$，また，$du = (\beta + \frac{\Delta^{2}}{2})^{-1} dz$．$u=0$のとき，$z=0$，$u \to \infty$で$z \to \infty$．

$$
\int_{0}^{\infty} z^{\frac{d}{2} + \alpha -1} ( \beta + \frac{\Delta^{2}}{2} )^{-\frac{d}{2} -\alpha +1} \exp(-z) (\beta + \frac{\Delta^{2}}{2})^{-1} dz \
= ( \beta + \frac{\Delta^{2}}{2} )^{-\frac{d}{2} -\alpha} \int_{0}^{\infty} z^{(\frac{d}{2} + \alpha) -1} \exp(-z) dz.
$$
ガンマ関数の定義より，
$$
p_{Y}(\textbf{y}) \propto \Bigl( \beta + \frac{\Delta^{2}}{2} \Bigr)^{-\frac{d}{2} -\alpha} \Gamma \Bigl( \frac{d}{2} + \alpha \Bigr) \tag{18}
$$

$(17)$の$u$に依存しない項も考慮して，

p_{Y}(\textbf{y}) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} \frac{1}{(2\pi)^{\frac{d}{2}}}  \frac{1}{\sqrt{\det(\Sigma)}} \Bigl( \beta + \frac{\Delta^{2}}{2} \Bigr)^{-\frac{d}{2} -\alpha}  \\
= \frac{\Gamma \Bigl( \frac{d}{2} + \alpha \Bigr)}{\Gamma(\alpha)}\frac{\beta^{\alpha}}{(2\pi)^{\frac{d}{2}}} \frac{1}{\sqrt{\det(\Sigma)}} \Bigl( \beta + \frac{\Delta^{2}}{2} \Bigr)^{-\frac{d}{2} -\alpha} \Bigl( \frac{1}{\beta} \Bigr)^{\frac{d}{2} + \alpha} \beta^{-\frac{d}{2}-\alpha} \\
= \frac{\Gamma \Bigl( \frac{d}{2} + \alpha \Bigr)}{\Gamma(\alpha)}\frac{1}{(2 \beta \pi)^{\frac{d}{2}}} \frac{1}{\sqrt{\det(\Sigma)}} \Bigl( 1 + \frac{\Delta^{2}}{2 \beta} \Bigr)^{-\frac{d}{2} -\alpha}. \tag{19}

ここで，$\alpha = \beta = \frac{\nu}{2}$，$p = d$とおくと，
$$
p_{Y}(\textbf{y}) = \frac{\Gamma \Bigl( \frac{\nu+p}{2} \Bigr)}{\Gamma \Bigl( \frac{\nu}{2} \Bigr)}\frac{1}{(\nu \pi)^{\frac{p}{2}}} \frac{1}{\sqrt{\det(\Sigma)}} \Bigl( 1 + \frac{\Delta^{2}}{\nu} \Bigr)^{-\frac{(\nu+p)}{2}}, \tag{20}
$$
となり，$(1)$のt分布の定義と一致します．$\Box$

実践

Pythonによる乱数発生の実装

$(2)$式がそのまま乱数の生成方法なので，これをpythonで実装します．

# -*- coding: utf-8 -*-
#!/usr/bin/python

import numpy as np
import matplotlib.pyplot as plt

#パラメーターをセットする．
N = 5000
d = 10
df = 4

mean = np.zeros(d)
cov = np.eye(d)

#ガンマ分布からの乱数生成
V = np.random.gamma(shape=df/2., scale=df/2.,size=N)

#多変量正規分布からの乱数生成
X = np.random.multivariate_normal(mean=mean, cov=cov, size=N)

#Xを変換する．
V = V.reshape((N,1))
denom = np.sqrt(np.tile(V,d))
Y = mean + X / denom


#比較用の多変量正規分布からの乱数を発生させる．
#（疑問:比較用はこんな感じでいいのだろうか？）
cov_ = ((df - 2) / float(df)) * np.corrcoef(Y.T)
X_ = np.random.multivariate_normal(mean=mean, cov=cov_, size=N)

#プロットする．
fig = plt.figure()
ax = fig.add_subplot(111)
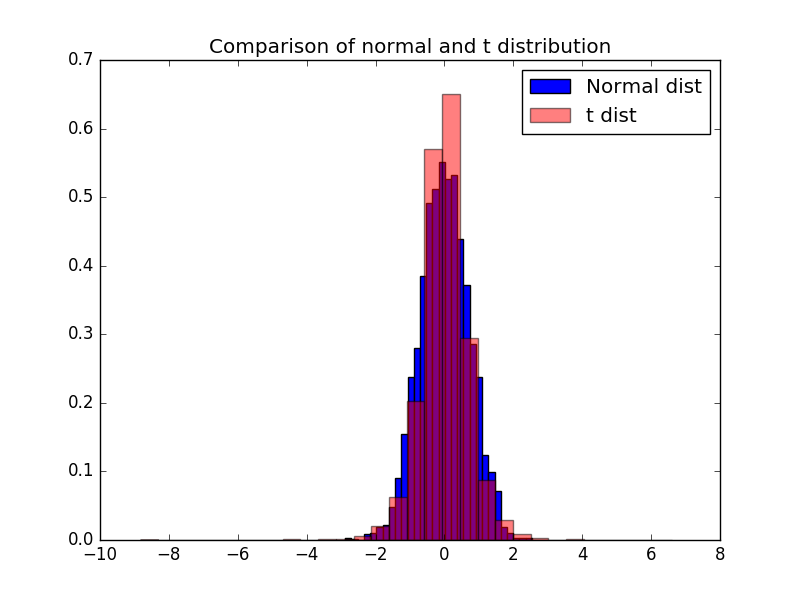
ax.hist(X_[:,0], color="blue", normed=True, label="Normal dist", bins=30)
ax.hist(Y[:,0], color="red", normed=True, label="t dist", bins=30, alpha=0.5)
ax.set_title("Comparison of normal and t distribution")
ax.legend()
fig.show()

fig = plt.figure()
ax = fig.add_subplot(111)
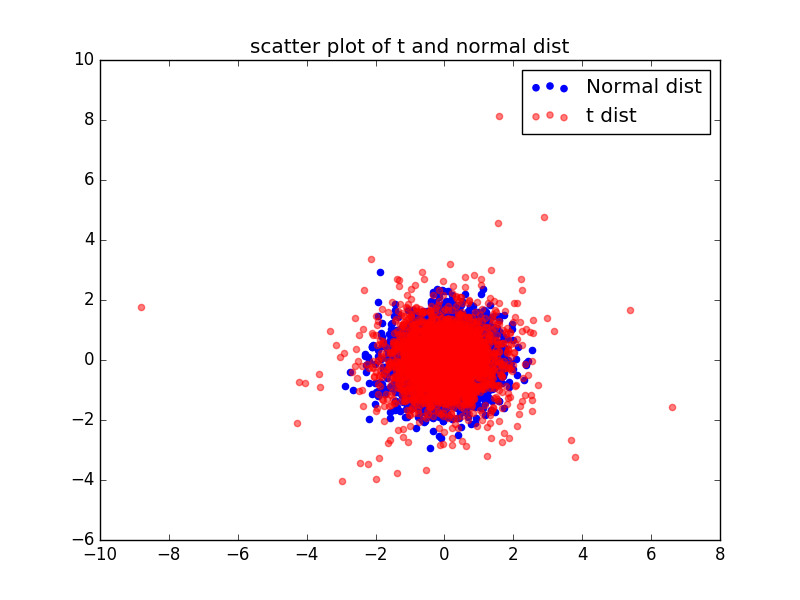
ax.scatter(X_[:,0], X_[:,1],color="blue",label="Normal dist")
ax.scatter(Y[:,0], Y[:,1],color="red",label="t dist",alpha=0.5)
ax.set_title("scatter plot of t and normal dist")
ax.legend()
fig.show()

分散も大きいしt分布っぽいかな？
（一次元ずつ以外の比較もしたかったけど，書き直して力尽きたのでこのくらいで...）

最後に

雰囲気数学マンなので間違っていたら教えてください．
時間があればいろいろな分布のつながりを追ってみたいなあ．