はじめに
『オブジェクト指向における再利用のためのデザインパターン』(通称GoF本)で紹介されているStrategyパターンをPythonのデコレータを使って実装する話です。この方法は『Fluent Python』を読んで出てきたので、自分でもちょっと真似してみました。
Strategyパターンとは
「一連のアルゴリズムを定義し、それぞれをカプセル化して交換可能にします。クライアントはアルゴリズムを個別に呼び出すのではなく、単一のインタフェースを通じて使うアルゴリズムを変えられます。」
というようなことが、GoF本には書いてあった気がします。
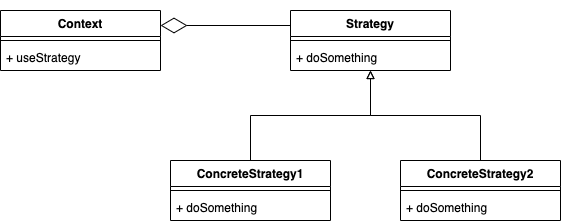
クラス図
- Context:それぞれアルゴリズムを実装したConcreteStrategyに処理を移譲します。
- Strategy:各アルゴリズムを実装するコンポーネントに共通のインタフェースを提供します。
- ConcreteStrategy:Strategyを実装してアルゴリズムを実現します。
Pythonでは
PythonにJavaのようなインタフェースはないので代わりに、abcモジュールの抽象基底クラス(Abstract Base Class; ABC)をStrategyクラスが継承して、そのdoSomethingメソッドにabstractmethodデコレータを付けるというのが正統な気がします。
一方で、ConcreteStrategyクラスがメンバ変数を持たず、Contextから受け取る情報を処理するメソッドを1つだけ持つ場合があります。すると、インタフェースもどきを作って継承して実装するというのはPythonとしては大仰すぎるという話になります。その場合は、ConcreteStrategyのメソッドを関数に取り出して、それを取りまとめることでStrategyパターンを実現する方法が考えられます。
実際にやってみた
1週間前のアドベントカレンダーで作ったロウソク足表示ダッシュボードの記事です。その中で、株価の終値から単純移動平均線(コードのcalc_SMA)を計算した図を載せていました。
単純移動平均線は株価のトレンド、高騰しているのか下落しているのか、を可視化している線です。が、これ以外にも指数平滑移動平均線や線形回帰を利用した手法などがあるので、それも並べて実装したのがcalc_EMAとcalc_LRIです。
from sklearn.linear_model import LinearRegression
trend_calculators = {} # トレンド分析を計算する関数を格納する辞書
def trend_calculator(name):
"""トレンド分析を計算する関数を登録する
デコレータとして使い、nameがキーで関数がバリューの辞書を作る
Args:
name (str): トレンド分析の名前
Returns:
function:
"""
def _trend_calculator(calc_fn):
trend_calculators[name] = calc_fn
return calc_fn
return _trend_calculator
def select_calculator(name):
"""トレンド分析の手法を選択する
Args:
name (str): 手法の名前
Returns:
function: トレンド分析を計算する関数
"""
return trend_calculators[name]
@trend_calculator("simple")
def calc_SMA(df, num):
"""単純移動平均線(Simple Moving Average)を計算する
Args:
df (pandas.DataFrame): 株価情報(日付、始値、終値、高値、安値、出来高)
num (int): 移動平均を取る期間
Returns:
list: dfが持つ日付期間で単純移動平均を計算した値を格納したリスト
"""
averages = []
for i in range(len(df)):
if i >= num-1:
averages.append(df.loc[i-num+1:i,"終値"].sum()/num)
else:
averages.append(None)
return averages
@trend_calculator("exponential")
def calc_EMA(df, num):
"""指数平滑移動平均線(Exponential Moving Average)を計算する
Args:
df (pandas.DataFrame): 株価情報(日付、始値、終値、高値、安値、出来高)
num (int): 移動平均を取る期間
Returns:
list: dfが持つ日付期間で指数平滑移動平均を計算した値を格納したリスト
"""
averages = []
for i in range(len(df)):
if i == num-1:
averages.append(df.loc[i-num+1:i,"終値"].sum()/num)
elif i > num-1:
ema = averages[i-1]+2/(num+1)*(df.loc[i,"終値"]-averages[i-1])
averages.append(ema)
else:
averages.append(None)
return averages
@trend_calculator("regression")
def calc_LRI(df, num):
"""線形回帰値線(Linear Regression Indicator)を計算する
その日からnum-1日前のデータで線形回帰を行い、その日の値を推論した値
Args:
df (pandas.DataFrame): 株価情報(日付、始値、終値、高値、安値、出来高)
num (int): 線形回帰のデータを取る期間
Returns:
list: dfが持つ日付期間で線形回帰値を計算した値を格納したリスト
"""
averages = []
for i in range(len(df)):
if i >= num-1:
model = LinearRegression()
X = [[j] for j in range(num)]
y = df.loc[i-num+1:i,"終値"].to_list()
model.fit(X,y)
averages.append(model.predict([X[-1]])[0])
else:
averages.append(None)
return averages
デコレータのtrend_calculatorがそれぞれのトレンド分析関数を名前と紐づけて登録してくれます。新しい分析関数を追加するのも同じように簡単にできます。クライアントはselect_calculatorを使って好きな分析関数に処理をお願いできます。select_calculatorがクラス図のContextに相当すると言う感じですね。
終わりに
ざっくり説明してコードをペッと貼り付けてしまったので、説明が雑ですがご了承下さい![]()
興味を持った方は『Fluent Python』も読んでみてください![]()
Strategyパターンのstrategyが状態を持つ必要がないなら、関数を使って書けるらしいですよと言う話でした。