書誌情報
著者:Kun Xu, Lingfei Wu, Zhiguo Wang, Yansong Feng, Michael Witbrock, Vadim Sheinin
所属:IBM Research
arXiv: 2018/5/25
概要
- グラフ構造から出力センテンスを生成する graph-to-sequence neural encoder-decoder architecture を提案
- 既存のグラフ情報をシーケンスに落としてから Seq2Seq にかけるアプローチではグラフの情報が失われてしまう
- 入力センテンスの句構造情報を抽出して用いる Tree2Seq [17] や,入力センテンスを木構造として階層的にencode する方法も提案されている[19,20]が,こうしたモデルは適用対象が限定され,グラフ構造一般の問題に適用可能ではない
- bAbI task19, グラフからの最短経路抽出, SQLからの質問文生成タスクにおいて,既存のグラフ構造を考慮した GraphConvolutionNetwork 等を上回るパフォーマンスを示した.
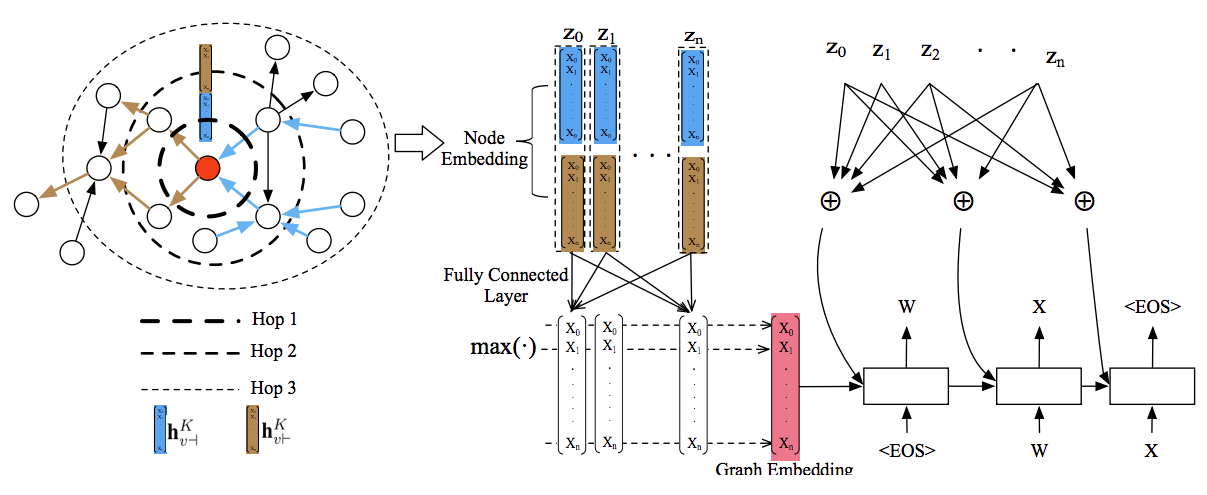
Graph2Seq model
モデルは3つの要素から構成される
1. Node Embedding
- 入力グラフから,各node を表現するベクトルを計算
2. Graph Embedding
- node embedding をまとめて グラフ全体を表現とするベクトルを計算する
3. Attention based decoder
- Graph Embedding を入力とする Attention付きDecoder
- Node embedding に対して各ステップでAttention を計算
Node Embedding Generation
- ノード $v$ のテキスト情報とEmbedding行列 $W_e$ から 特徴ベクトル$a_v$ を作成
- ノード $v$ に隣接するノードを forward neighbors $N_{\vdash}(v)$, backward neighbors $N_{\dashv}(v)$ に分類
- $N_{\vdash}(v)$ : 有向グラフにおいて,ノード $v$ からエッジが出ているノード群
- $N_{\dashv}(v)$ : 有向グラフにおいて, ノード $v$ へとエッジを出しているノード群
- ノード $v$ のforward neighbors の k-1 ステップでの forward representation $h^{k-1}_{u\vdash}, \forall u \in N_{\vdash}(v) $ を一つにまとめたベクトル neighborhood vector $h^k_{N(v)}$ を作成する
- k はイテレーションの回数を示している
- 一つにまとめる操作を $\mathrm{AGGREGATE}^{\vdash}_k$ とよび,いくつかの種類を試す
- ノード $v$ の現在の forward representation $h^{k-1}_{v\vdash}$ と,ステップ3で作成した neighborhood vector $h^k_{N\vdash(v)}$ を Concat する.このConcat したベクトルを非線形な活性化関数を持つ全結合NN に入力して得られた出力をノード $v$ の新たな forward representation $h^k_{v\vdash}$ とする.
- 同様にしてノード $v$ のbackward representation $h^k_{v\dashv}$ を更新する
- ステップ 3~5 を $K$ 回繰り返す. 最後に得られたノード $v$ の forward representation と backward representation を Concat したものを ノード $v$ の表現ベクトル(node embedding)とする
Aggregator Architectures
隣接するノードの表現ベクトルを用いて1つのベクトルを作成する方法(AGGREGATOR)にバリエーションを用意して検証した.
- Mean aggregator : 隣接するノードの表現ベクトルを平均したものを出力する
- LSTM aggregator : LSTM に 隣接するノードの表現ベクトルをランダムな順番で入力し,最後のLSTMセルの隠れ状態を出力とする
- Pooling aggregator : 隣接ノードの表現ベクトルそれぞれを全結合層に入れ,出力ベクトルを各要素毎に max-pooling したものを出力とする
Graph Embedding Generation
node embedding からグラフ全体の情報を表す graph embedding を作成する
Pooling-based Graph Embedding
- node embedding をそれぞれ全結合層に入れ,出力を要素ごとに max-pooling, min-pooling, もしくは averatge-pooling したものを graph embedding とした.実験した結果ときにさはなかったので max-pooling をデフォルトとした
Node-based Graph Embedding
- 入力グラフに,全てのノードから入力を受ける super node $v_s$ を追加
- node embedding の計算の際に同様に $v_s$ のembedding も計算し, それを graph-embedding とした
Attention Based Decoder
- Graph embedding を入力とするRNNモデルで decodeする
- 従来のAttention モデル同様,1ステップ前の decoder隠れ状態と, 各ノードの表現ベクトルから $z_i$ アテンションを計算.計算した attention から $z_i$ を重み付き和したベクトル $c_i$(コンテキスト)を計算し,RNN出力の計算に使用
- ビームサイズ=5
c\_i = \sum^{V}_{j=1}\alpha_{ij}z_j, where \alpha_{ij}=\frac{\mathrm{exp}(e_{ij})}{\sum^{V}_{k=1}\mathrm{exp}(e_{ik})}, e_{ij} = a(s_{i-1}, z_j)
実験結果
bAbI Task 19
- bABi artificial intelligence task:AI の推論能力を測るためのタスク
- Task19(Path Finding)
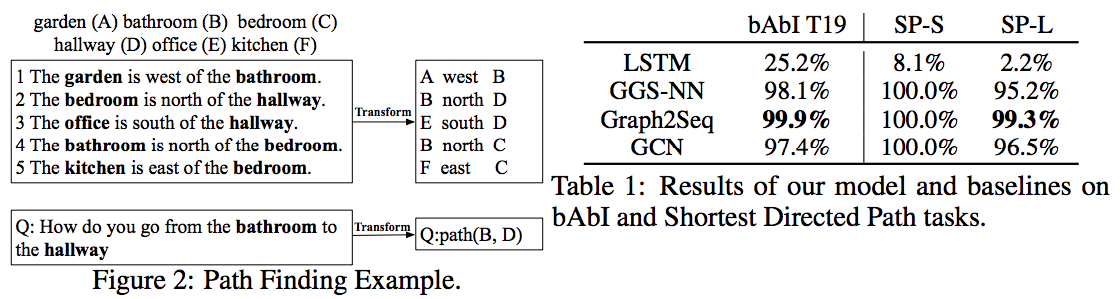
- 自然文で場所の位置関係が与えられ,ある場所から別の場所に行くための経路を答える課題 (Fig2 を参照)
- モデルに合わせてデータを整形
- 入力される場所の相対的な位置関係をグラフ化 (各場所をノード,位置関係をエッジとした)
- 例: A west B -> ノード A から ノード B に向かってエッジ west が張られているグラフ
- タスクは相対的な位置情報から構築されるグラフにおいて,ある2つのノード間の最短経路を求める問題とみなせる
- 質問文が ノード $N_{o1}$ から ノード $N_{o2}$ への最短経路を求める場合 $N_{o1}$, $N_{o2}$ の text attribute を START, END とし,他のノードの text attribute はグラフ内のID とした
- 各エッジはノードに変換し,エッジのテキストをそのノードの text attribute とした.
- エッジもノード化することで node embedding で node 同様に扱う
- 入力される場所の相対的な位置関係をグラフ化 (各場所をノード,位置関係をエッジとした)
- GraphConvolutionNetwork は sequence decoder と組み合わせることで シーケンスを出力させた.
結果
- Graph2Seqモデルが最も高い精度を示した(Table1, bAbIT19 列)
- GCN は無効グラフに対してデザインされており,有効エッジの情報が失われてしまうために Graph2Seqよりも精度が低くなっていると考えられる
Shortest Path Task
- ランダムに生成した有効グラフの中で2つのノードの最短パスを見つけるタスク
- データセットの作成:ランダムにグラフを作成し,その中から2つのノードを選択
- 最短パスは1経路のみであるとする
- Small(node数=5, 最短パス長>=2), Large(node数=100, 最短パス長>=4) の2種類の設定で作成
結果
- Graph2Seqモデルが最も高い精度を示した(Table1, SP-S, SP-L 列)
- GGS_NN は長い距離の依存関係を扱うことが難しいため Large グラフで精度が低下
- GCN は有向グラフを考慮できないため精度が下がる
- 有効性を考慮できないのであればもっと低くなってもおかしくないのでは??
Natural Language Generation Task
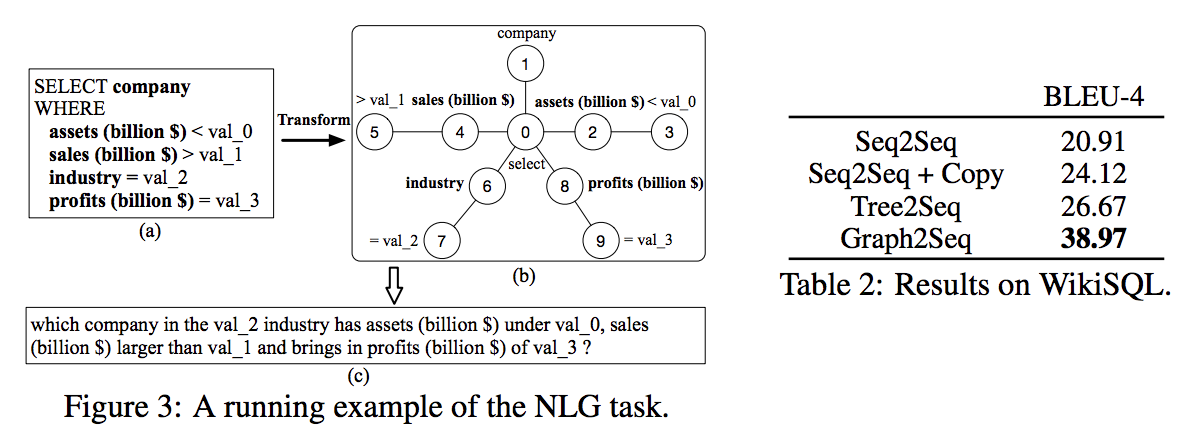
- SQL を 文章に変換するタスク
- graph-to-sequence モデルを意味構造を表現するグラフに対して適用
- WikiSQLデータ・セットを使用
- 87,726 の人手で作成された自然言語質問文と,対応するSQLのデータセット
- SQL を入力として,正しい英語の質問文を生成するタスクとした(本来は逆の用途で作成された)
- BLEU4 スコアで評価
- 各モデルに合わせて入力を加工
- Tree2Seq : SQL を木構造に変換した上で入力
結果
- Graph2Seq が最も高い精度示した (Table2)
- Tree2Seq の tree encoder では子ノードの情報しか統合できず,親ノードの情報が失われてしまうため,精度が低くなったと考えられる
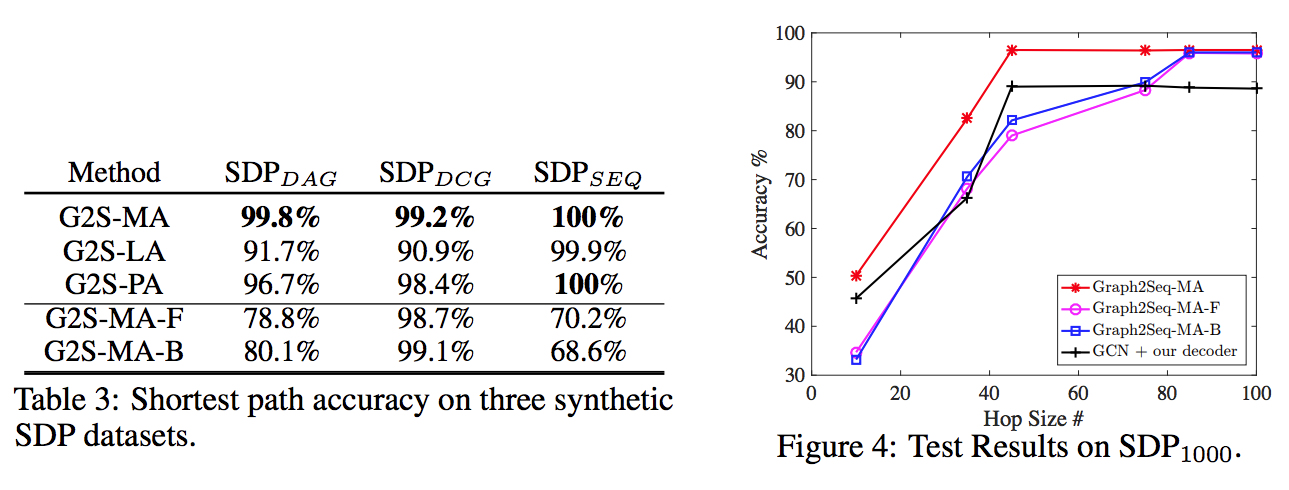
Aggregator と Hop Size について Shortest Path Taskで比較
- Mean Aggregator が最も高いパフォーマンスを示した
- Hopサイズが大きくなるほど精度は向上 (ノード数1000のグラフで実験)
- forward, backward 両方の情報を用いる MA が Hop数に対して高いパフォーマンスを示す
- Graph2Seqでは hop数を大きくすれば全て同じパフォーマンスに収束
- Methodの違い
- MA=mean aggregator, LA=LSTM, PA=Pooling, MA-F=mean aggregator with forward repr only
- 各列の違い
- DAG : directed acyclic graph, グラフ内に循環が存在しない
- DCG : directed cyclic graph, グラフ内に循環が存在
- SEQ : sequence, グラフは一本の線になっている