クリーンコードやクリーンアーキテクチャなどの「クリーン」シリーズでお馴染みのUncle Bobの新刊です。クリーンは書籍タイトルに付きませんでした。
本書は関数型プログラミングに関する書籍ですが、関数型プログラミング言語と聞いて、真っ先に皆が思い浮かべるものではないであろうClojureを取り上げて、一貫してこれとオブジェクト指向プログラミング言語との比較がされています。
これは読み進めていくと、オブジェクト指向言語としてはC++やJavaを用いて、Clojureのコードを対比していくという構図を随所でとっており、これらとできるだけ距離の遠い言語を選びたかったのだな、というのが分かります。Clojureは関数型であり動的型付け言語です。この2つの面で対比されており、本書の半分は静的型付けと動的型付けの話な印象があります。
関数型におけるSOLID
関数型プログラミングとは何か、という観点については『Functional Design』よりも分かりやすく詳細な書籍は多くあるので、感想・考察は省略します。
この書籍で重要なのは、過去Uncle Bobが牽引してきた設計論に関してのアップデート(というかマッピングかも)にあります。
これまでのUncle Bobの著作はオブジェクト指向設計を暗黙のうちに仮定しており、提唱するSOLID原則も(それぞれの元にしたものもオブジェクト指向設計分野の研究だったこともあり)、それを前提にしたものでした。
本作では12章にて、関数型プログラミングでSOLIDの原則を再考するという試みがなされています。(また、16章ではデザインパターンに関しても同様の取り組みをしており、本記事では割愛しますが、こちらも興味深いです。)
単一責任原則(SRP)
単一責任原則はSOLIDの中でも、その曖昧さゆえに多くの批判も受けてきました。
モジュールを変更する理由はたったひとつだけであるべきである
と説明されますが、これだけでは説明不足で、
モジュールはたったひとつのアクターに対して責務を負うべきである。
までを言わないと判然としないところがあります。
『Functional Design』の中でのSRP違反の例は、1つの関数の中に複数の責務が混ざっているぞ、ということを言いたいらしいのですが、この例ではタイプバリデーションとセマンティックバリデーションの曖昧な境界の問題をまた含んでしまうので、良い例ではありません。
(defn validate-customer
[{:keys [id name address credit-limit] :as customer}]
(if (or (nil? id) ;; データの型チェック(必須チェック)
(nil? name)
(nil? address)
(nil? credit-limit))
:invalid
(let [credit-limit (Integer/parseInt credit-limit)]
(if (> credit-limit 50000) ;; 与信額の上限チェック
:invalid
(assoc customer :credit-limit credit-limit)))))
結局のところ、SRPは「凝集度高くしましょうね」ということを言ってるに過ぎないのですが、ずっと上手く説明できていない印象です。
一方でTidy First?でのKent Beckの説明 はわかりやすいです。
- ソフトウェアのコストを下げる → 結合を減らす必要がある
- 結合を減らすのもコストがかかる → トレードオフが大事
- 結合全てを解消できない → 結合しているものは、できるだけひとまとまりになっていて欲しい(凝集)
関数型の観点では、先に紹介したDan NorthのCUPIDで整理されている「Composable」のためにSRPすなわち凝集性は重要です。SRPはオブジェクト指向だけの話ではなく、関数型プログラミングでも同じく重要です。
オープンクローズドの原則(OCP)
OCPはポリモーフィズムそのものを言い表した原則と言えるので、何らかの多態を実現する仕組みがあれば、そこにオブジェクト指向も関数型もありません。
『Functional Design』の例を借りると、以下のようなcopy関数は、標準入力から一行読み込むread-lineや標準出力に一行書き込むprintlnに依存しています。
(defn copy []
(let [line (read-line)]
(if (= line "")
nil
(do
(println line)
(recur)))))
したがって、これをファイルから読み込みにも対応させたいという機能追加要求に対して、この関数を修正して対応するとOCP違反になります。OCP違反の何が不味いかというと、既存コード部分は仕様変わっていないのに、そこを修正すると既存機能に影響ないことまで保証する必要が出てくるためです。
OCPに違反しないようにするためには、動的ディスパッチができればいいのですが、これはサブタイピングを使わなくてもいくつかのやり方があります。最もシンプルなのは、外から実装の詳細を与えてあげる、すなわち1行読み込む関数と1行書き込む関数を引数に追加すれば良いです。
(defn copy [read write]
(let [line (read)]
(if (= line "")
nil
(recur read (do (write line) write)))))
また、Clojureではマルチメソッドという仕組みがあって、こちらは構造的にはオブジェクト指向のポリモーフィズムに近い。
標準入出力以外を読み書きする場合は、別の:device-typeに対応するdefmethodを追加すれば良いです。
;; インタフェース
(defmulti get-line (fn [device] (:device-type device)))
(defmulti put-line (fn [device line] (:device-type device)))
;; インタフェースに対して処理は実装する
(defn copy [device]
(let [line (get-line device)]
(if (= line "")
nil
(do
(put-line device line)
(recur device)))))
;; 実装の詳細
(defmethod get-line :console [device]
(read-line))
(defmethod put-line :console [device line]
(println line))
「拡張に対して開いていて、変更に対して閉じていている」というOCPの原則は、プログラミング言語のパラダイムによらず重要だが、実現の仕方は言語によって異なる、ということです。
リスコフの置換原則(LSP)
リスコフの置換原則については、元の論文がサブタイピングを前提として書かれたものなので、「関数型プログラミングでいうと…」を言うには、まずリスコフ置換原則を汎化する必要があります。が、『Functional Design』においては、まずそれが出来てないので、上手く説明できているとは言い難いです。
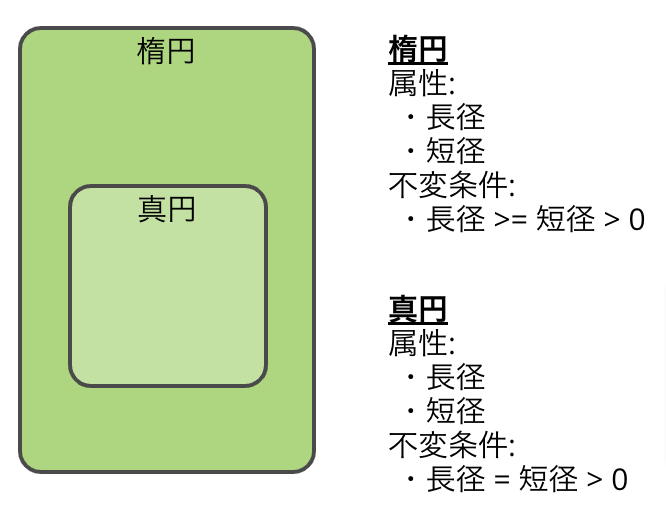
LSPの伝統的な例として、楕円-真円(『Functional Design』では長方形-正方形が例示されています)問題を考えます。Wikipediaにも専用ページがある有名な問題です。
数学的には真円は楕円の特殊型なので、楕円のサブタイプとして真円を考えられます。振る舞いとして面積を算出するメソッドだけであれば、真円も楕円も同じ振る舞いができるので、このサブタイプ関係は問題ありません。リスコフ置換原則を満たしています。
// 説明の都合上、Mutableな操作が可能かつ代数データ型が定義できる必要があるのでTypeScriptで例示
type 楕円 = 真円 | 真円でない楕円
const 面積計算 = (e: 楕円) => e.長径 * e.短径 * Math.PI
次に長径を引き伸ばす振る舞いを追加することを考えます。これは楕円には定義できますが、真円をx軸方向に引き伸ばすと、もうそれは真円ではない、真円の不変条件を満たさないので、リスコフ置換原則違反になります。引数に真円を渡すと、この関数適用した結果は真円の不変条件を満たさないからです。
// ミュータブルな定義
const 長径を引き伸ばす = (e: 楕円, dx: Number) => e.長径 = e.長径 + dx
ですが、「長径を引き伸ばす」をイミュータブルな操作だとすると、矛盾は起こりません。
const 長径を引き伸ばす = (e: 楕円, dx: Number) => new 楕円(e.長径 + dx, e.短径)
真円を引数に「長径を引き伸ばす」を適用すると「真円でない楕円」が返ります。オブジェクトに対する操作をイミュータブルにして、必要なら型が変わってもいい、というのはリスコフ置換原則を保ための1つの設計戦術です。
この時、「長径を引き伸ばす」操作は、結局楕円の定義域全てを受け取って、楕円の値域にマッピングしています。すなわち、イミュータブル版の「長径を引き伸ばす」だけの振る舞いにおいては、楕円 = 真円 | 真円でない楕円という分類は使っていません。
type 長径を引き伸ばす = (e: 楕円, dx: Number) => 楕円
一方で、ミュータブルな定義の方は、この操作が可能なものは「真円でない楕円」だけなので、以下のようになります。
// 楕円全体を渡すと例外が発生する
const 長径を引き伸ばす = (e: 楕円, dx: Number) => {
if (e.長径 === e.短径) throw Error(`真円は水平方向に引き伸ばせない`)
e.長径 = e.長径 + dx
}
// 「真円でない楕円」だけを受け取るようにすれば例外は発生しない
const 長径を引き伸ばす = (e: 真円でない楕円, dx: Number) => {
e.長径 = e.長径 + dx
}
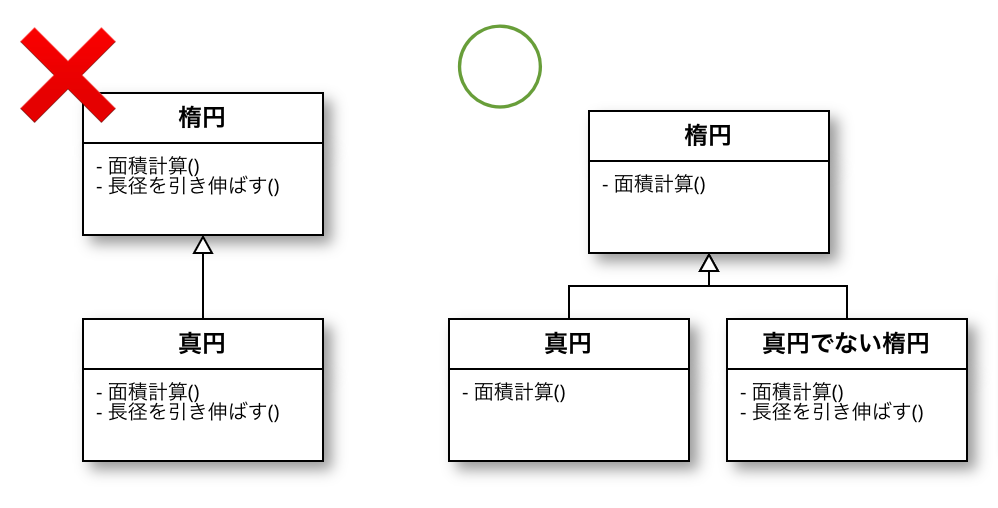
LSPに違反するオブジェクト指向のコードでは、サブタイプのメソッドを呼ぶと例外が発生します。
したがって、型階層を見直す必要があるのですが、結果として代数データ型を使った楕円 = 真円 | 真円でない楕円 と同じ構造になります。すなわち、型階層をLSPに違反しないように構成することは、例外が発生しないように型定義していくことに他なりません。例外を発生させることなく、関数の引数の定義域全てに対応できる性質を全域性と呼びます。
LSPを一般化すると、「振る舞いは、対象の型の定義域に全てに対応しなければならない(全域性を持たなければならない)」といえます。
関数型プログラミングでは、必ずしも全域性を満たさなきゃいけない原則ってわけではありませんが、追加のメリットがあるので、積極的に検討する価値はあります。
インターフェイス分離原則(ISP)
インターフェイス分離原則は、関数が所属するネームスペースとしてインタフェースを使うような言語のために必要な原則であって、元々SOLIDの原則の中でも適用される範囲が狭いものです。
「関数が所属するネームスペースとしてインタフェースを使うような言語」でなければ、関数をどのモジュールに配置するのが適切か、という問題に汎化できるので、単一責任原則(SRP)と等価といえます。
DIP
DIPはUncle Bobがクリーンアーキテクチャを提唱するうえで、そこに直結する概念で、「抽象度の高いモジュールは、自身より抽象度の低いモジュールに依存してはならない」ということを言っているに過ぎません。これに違反すると、OCP違反と同じデメリットが発生します。
抽象度を何と定義するか次第なところもあります。クリーンアーキテクチャの本では、ビジネスロジックの方が抽象度が上であって、データベースとのやりとりやHTTPリクエスト/レスポンスのやりとりは抽象度が低いという前提を置いているので、その元でDIP原則にしたがえば、あの同心円の図になるだろう、ということです。
ということで、DIPはオブジェクト指向前提の話ではなく、どこで抽象と具体を切り分けるか、切り分けた以上、抽象が具体に依存してはならない、ということを意味します。「抽象が具体に依存してはならない」の実現手段は、外から実装の詳細を貰ったり、インターフェイスを介してポリモーフィズムを実現するOCPのセクションで書いたコードと同じになります。
まとめ
『Functiuonal Design』は関数型プログラミングの本として捉えると、他にもっと分かりやすくて良い本はあるよね、となるけれども、SOLID原則やデザインパターンのような、その時代背景から暗黙的にオブジェクト指向を前提としてきた設計原則・プラクティスをより高次の視点から見つめ直すきっかけを与えてくれる本としては貴重なもので、それをUncle Bobが書いたことに大変意義があると評価します。