実は奥が深い無安定マルチバイブレータの発振周波数（より厳密な式を導いてみた）

電子工作や学生実験などで，実装した無安定マルチバイブレータの発振周波数（または発振周期、パルス幅）が理論値と大幅に外れてしまい，実装が上手くいかなかったりレポートの考察で困ったりしたことはありませんか？

私もその中の一人だったのですが，最近趣味にしていた無安定マルチバイブレータの考察において、発振周波数のより厳密な式を導出することができました．

その結果，誤差は大幅に改善し，よく知られている理論式通りの発振周波数になる条件が実はかなり厳しいことが判明したので，忘備録もかねて共有させていただきます．

この式を使えばレポートの考察も捗るかもしれません！！
式の導出もできるだけ詳しく書いてます．

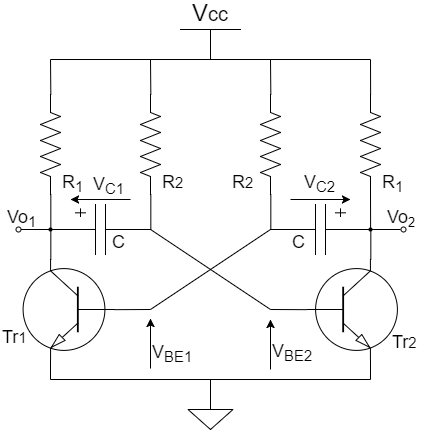
回路図

今回扱う回路の抵抗やコンデンサの値は左右対称で，LEDは使用しないものとします．LEDがある場合でも，簡易式の導出に影響がないのでそのまま使用できます．

※LED有の回路だとコンデンサの漏れ電流がすごく大きな影響を与えるのですが，それについてはいずれ記事として報告したいと考えてるところです．

回路図の作成には，Web上で図の作成ができるdraw.ioを使用しました．とてもおすすめです．

図１．無安定マルチバイブレータ（左右対称，LEDなし）

#結論をあらかじめ
以下に式を示します．これらの式が実際にどれくらいの誤差になるのかを，測定結果として記事の一番最後に示してあります．
注意：スマートフォンでは数式が途切れて表示される場合がありますが，数式部を横スクロールすることで全体を見ることができます(横画面推奨)．

理論式_簡易版

図１の発振周波数$f_\mathrm{osc}$及び発振周期$\mathrm{T}$は，
発振周波数：

f_{\mathrm{osc}} = \frac{1}{2CR_2 \cdot \ln{2}} \fallingdotseq \frac{1}{1.386CR_2} \, \mathrm{[Hz]} \tag{A-1}

発振周期：

\mathrm{T} = 2CR_2 \cdot \ln{2} \fallingdotseq 1.386CR_2 \, \mathrm{[sec]} \tag{A-2}

となる．

この式は誤差がすごく大きいのが欠点です．

##理論式_厳密版
図１の発振周期$\mathrm{T}$は，

\begin{align} \left\{ \begin{array}{lll}
V^\mathrm{A}_\mathrm{c1(t=0)}&= (V_\mathrm{cc}-V_{\mathrm{th}}) \left\{ \exp{\left( \frac{1}{2CR_2}\mathrm{T} \right)} - 1 \right\} - V_{\mathrm{th}}+V_\mathrm{CE(SAT)} \tag{B-1} \\
V^\mathrm{B}_\mathrm{c1(t=0)}&= \left( V_\mathrm{cc}- V_\mathrm{BE2(ON)}+ V_\mathrm{th}-V_\mathrm{CE(SAT)} \right) \left\{ 1- \exp{\left( -\frac{1}{2CR_1}\mathrm{T} \right)} \right\}- V_\mathrm{th}+V_\mathrm{CE(SAT)} \\
V^\mathrm{A}_\mathrm{c1(t=0)}&= V^\mathrm{B}_\mathrm{c1(t=0)}
\end{array} \right. \end{align}

の連立方程式を$\mathrm{T}$について解くことで得られる．

但し，$V_{\mathrm{th}}$は，Tr.がOFF状態からON状態に変わるのに必要な$V_\mathrm{BE}$，$V_\mathrm{CE(SAT)}$はコレクタ - エミッタ間飽和電圧，$V_\mathrm{BE2(ON)}$は，Tr.がON状態の時の$V_\mathrm{BE}$である．

この方程式は複雑なので，方程式を解くプログラムを書くなどしないといけないですが，誤差が簡易式と比較して非常に小さいです．
抵抗値に条件を持たせると以下のようになり，Excelなどで簡単に結果が得られます．

##理論式_厳密版（条件を満たす場合）
条件$R_2 >> R_1$を満たすとき，図１の発振周波数$f_\mathrm{osc}$及び発振周期$\mathrm{T}$は，(B-1)式より
発振周波数：

f_\mathrm{osc} \fallingdotseq \left( 2CR_2 \ln{\frac{2V_\mathrm{cc}- V_\mathrm{BE2(ON)}-V_\mathrm{CE(SAT)} }{V_\mathrm{cc}- V_\mathrm{th}}} \right)^{-1} \, \mathrm{[Hz]} \tag{C-1}

発振周期：

\mathrm{T} \fallingdotseq 2CR_2 \ln{\frac{2V_\mathrm{cc}- V_\mathrm{BE2(ON)}-V_\mathrm{CE(SAT)}}{V_\mathrm{cc}- V_\mathrm{th}}} \, \mathrm{[sec]} \tag{C-2}

と近似できる．

但し，$V_{\mathrm{th}}$は，Tr.がOFF状態からON状態に変わるのに必要な$V_\mathrm{BE}$，$V_\mathrm{CE(SAT)}$はコレクタ - エミッタ間飽和電圧，$V_\mathrm{BE2(ON)}$は，Tr.がON状態の時の$V_\mathrm{BE}$である．

この式の誤差は簡易式と比較して小さいですが，抵抗値の条件を満たす必要があります．
条件は$R_2 > 10R_1$位あれば十分です．

#よく知られている理論式の導出をおさらいしてみる
無安定バイブレータの本質は，コンデンサ$C$と抵抗$R$による充放電によって引き起こされる，トランジスタのスイッチング動作です．

※すごく長いので読み飛ばし推奨です．
※本記事では動作原理をめちゃくちゃ省略しています．動作原理の詳細は教科書や詳しいWebサイトをご参照ください．

##導出過程
###前提
まず，図１の回路はすでに発振しており，トランジスタ1（以下Tr.1と略します）がOFF状態からON状態に，Tr.2がON状態からOFF状態に変化した瞬間を考えます．また，この瞬間の時刻を$t=0 , \mathrm{[sec]}$とします．

$t=0$における左側のコンデンサ$C$の電圧$v_\mathrm{c1}$は，$t=0$になる以前，すなわちTr.1がOFFの間に図2で示す経路で充電されるので，

v_\mathrm{c1(t=0)}=V_\mathrm{cc}

となります．但し，Tr.2がON状態の時のベース - エミッタ間電圧 $V_{\mathrm{BE2(ON)}}$ を無視しています．

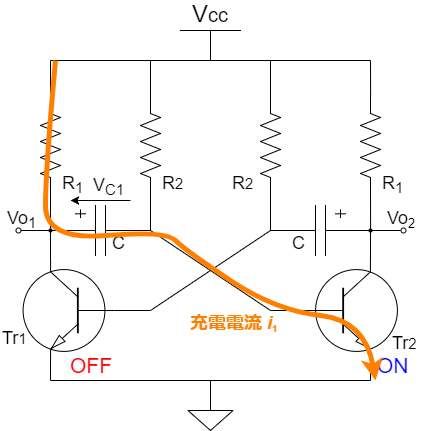
図２．$t=0$以前に左側のコンデンサが$V_\mathrm{cc}$になるまで充電されるの図

さらに，$t=0$以降の左側の出力電圧$v_\mathrm{o1}$は，Tr.1がON状態なので，

v_\mathrm{o1}=0 \; \; \; \;(但し，Tr_1=ON)

となります．その結果，図３に示す経路で左側のコンデンサは放電されます．

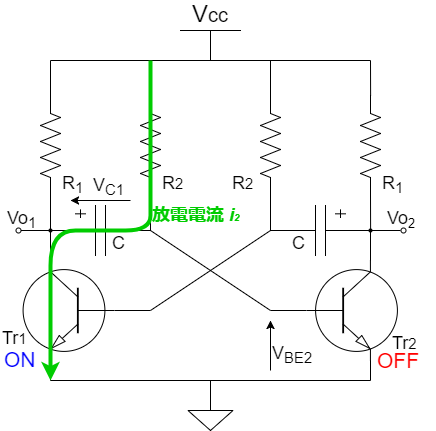
図３．$t=0$以降に左側のコンデンサが放電されるの図

回路方程式を立てる

次に，発振周期を求めるのに必要なベース - エミッタ間電圧 $V_{\mathrm{BE2}}$の時間変化を求めてみます．
図３より，回路方程式を求めます．

\begin{align} \left\{ \begin{array}{lll}
R_2i_2+ \frac{1}{C} \int i_2 \, dt = V_\mathrm{cc} \\
V_\mathrm{BE2(t)}= \frac{1}{C} \int i_2 \, dt
\end{array} \right. \end{align}

より，回路方程式は

CR_2 \frac{dV_\mathrm{BE2(t)}}{dt}+ V_\mathrm{BE2(t)}= V_\mathrm{cc} \tag{1.1} \\
\left( \because \int i_2 \, dt = CV_\mathrm{BE2(t)} \; \Rightarrow \; i_2= C\frac{dV_\mathrm{BE2(t)}}{dt} \right)

という微分方程式になります．
初期条件は

V_\mathrm{BE2(t=0)}= -V_\mathrm{cc} \tag{1.2}

です．

微分方程式を解く

$(1.1), (1.2)$の微分方程式を解いて，$V_\mathrm{BE2(t)}$を求めてみます．
今回は微分方程式を解くのにラプラス変換と逆ラプラス変換を用いてみました．
まずは$(1.1)$を次のように変形します．

\frac{dV_\mathrm{BE2(t)}}{dt}+ \frac{1}{CR_2}V_\mathrm{BE2(t)}= \frac{V_\mathrm{cc}}{CR_2}

$\mathcal{L}[V_\mathrm{BE2(t)}]=X(s)$としてラプラス変換すると，

\begin{align}
[sX(s)- V_\mathrm{BE2(t=0)}]+ \frac{1}{CR_2}X(s) &= \frac{V_\mathrm{cc}}{sCR_2} \\
sX(s)- (-V_\mathrm{cc})+ \frac{1}{CR_2}X(s) &= \frac{V_\mathrm{cc}}{sCR_2} \\
\end{align}

\begin{align}
X(s)&= \frac{ \frac{V_\mathrm{cc} }{CR_2}} {s(s+\frac{1}{CR_2})}- \frac{V_\mathrm{cc}}{s+\frac{1}{CR_2}} \\
\therefore X(s)&= \frac{V_\mathrm{cc}}{s}- \frac{2V_\mathrm{cc}}{s+\frac{1}{CR_2}} \;\;(部分分数分解した)
\end{align}

となります．これを逆ラプラス変換して変形すれば，

V_\mathrm{BE2(t)}= V_\mathrm{cc} \left\{ 1-2\exp{\left(-\frac{1}{CR_2}t\right)} \right\} \tag{1.3}

となり，$V_\mathrm{BE2(t)}$が得られました．
この式から，$V_\mathrm{BE2(t)}$は$-V_\mathrm{cc}$から$V_\mathrm{cc}$へ向かって徐々に変化しようとし，変化の速さは抵抗$R_2$及びコンデンサ$C$に依存することが分かります．

発振周期を求める

$V_\mathrm{BE2(t)}$が得られたので，いよいよ発振周期$\mathrm{T}$を求めます．

まず，Tr.2がOFF状態からON状態になるためには，$V_\mathrm{BE2} \geq 0$である必要があります．
したがって，$V_\mathrm{BE2(t)}$が$-V_\mathrm{cc}$から$0$になるまでの時間を求めれば，それが発振周期の半分$(\equiv \mathrm{T'})$となり，それを２倍すれば発振周期$\mathrm{T}$になります．

早速求めてみましょう．$(1.3)$の$V_\mathrm{BE2(t)}$に0を代入して変形すると，

0= V_\mathrm{cc} \left\{ 1-2\exp{\left(-\frac{1}{CR_2}\mathrm{T'}\right)} \right\} \\
\exp{\left(-\frac{1}{CR_2}\mathrm{T'}\right)}= \frac{1}{2} \\
-\frac{1}{CR_2}\mathrm{T'}= \ln{\frac{1}{2}} \\
\begin{align}
\therefore \mathrm{T'}&= CR_2\ln{2}
\end{align}

と求まります．したがって，発振周波数及び発振周期は，

f_{\mathrm{osc}} = \frac{1}{2CR_2 \cdot \ln{2}} \fallingdotseq \frac{1}{1.386CR_2} \, \mathrm{[Hz]} \tag{A-1}

\mathrm{T} = 2CR_2 \cdot \ln{2} \fallingdotseq 1.386CR_2 \, \mathrm{[sec]} \tag{A-2}

と求まりました！！

この式によると，発振周波数は抵抗$R_2$とコンデンサ$C$のみに依存するみたいです．
しかし，この結果は後ほど打ち砕かれます...

実測してみると...

##電源電圧を変化させてみる
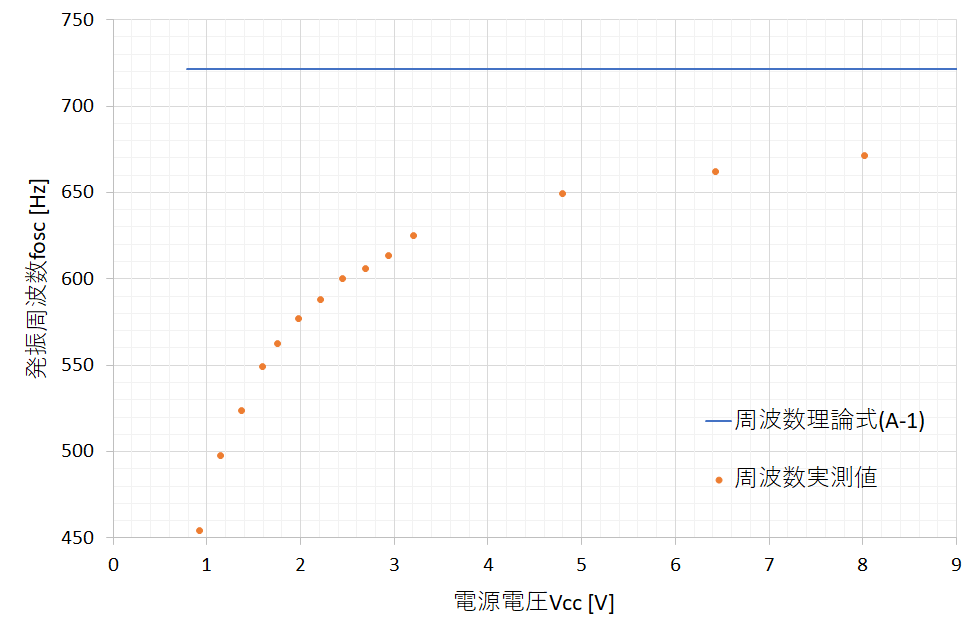
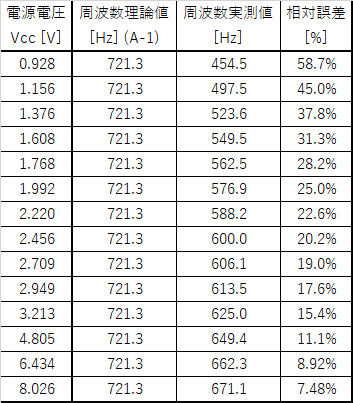
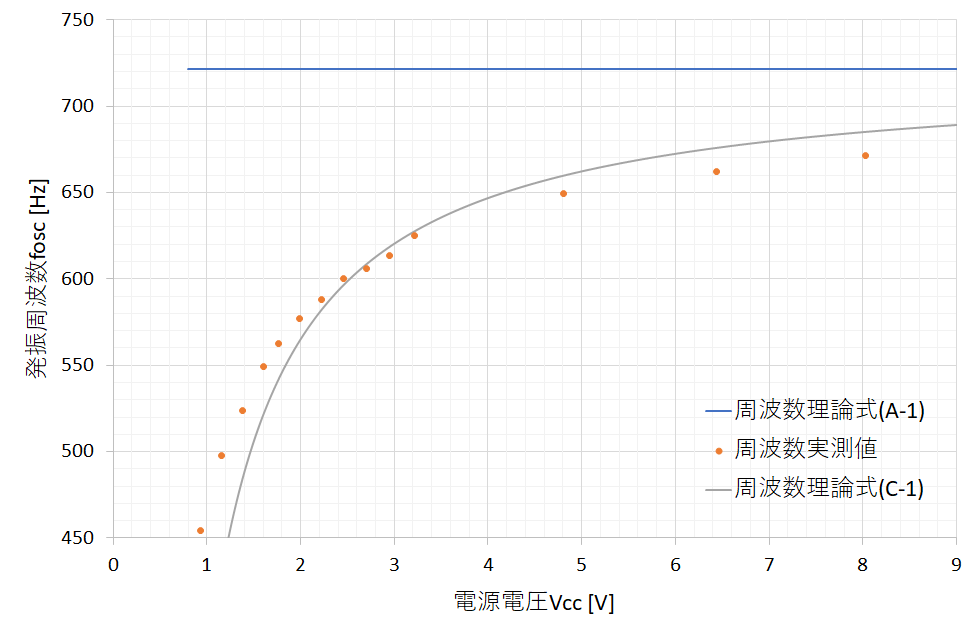
$R_1=1, \mathrm{[k\Omega]}, , R_2=10, \mathrm{[k\Omega]}, , C=0.1, \mathrm{[\mu F]}$（フィルムコンデンサ）, 使用トランジスタ：2SC1815(Y)という条件で，電源電圧を変化させながら発振周波数をアナログオシロで計測しつつ何点かプロットし，理論値と比較してみた結果が図４です．表１にデータも示します．
（ちなみに，$V_\mathrm{cc}$の値がぴったりじゃないのは電圧の可変手段としてショットキーバリアダイオードの電圧降下を利用したからです．電源電圧が時間変動していないことをアナログオシロで監視しつつ実験しました．）

図４．電源電圧を変化させてみた時の発振周波数

表１．電源電圧を変化させてみた時の発振周波数（データ）

この結果を見ると，発振周波数は理論式と全然合わず，しかも電源電圧$V_\mathrm{cc}$に依存していることがわかります．

##抵抗R1を変化させてみる
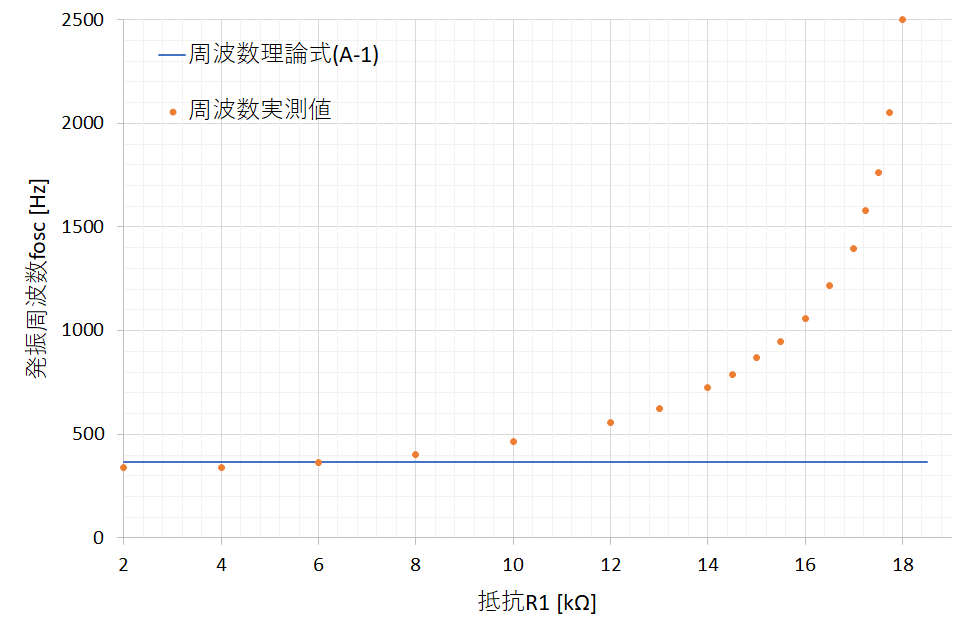
$V_\mathrm{cc}=8.0 , \mathrm{[V]}, , R_2=19.6, \mathrm{[k\Omega]}, , C=0.1, \mathrm{[\mu F]}$（フィルムコンデンサ）, 使用トランジスタ：2SC1815(Y)という条件で，抵抗$R_1$を変化させながら発振周波数をアナログオシロで計測しつつ何点かプロットし，理論値と比較してみた結果が図５です．表２にデータも示します．

図５．抵抗$R_1$を変化させてみた時の発振周波数

表２．抵抗$R_1$を変化させてみた時の発振周波数（データ）

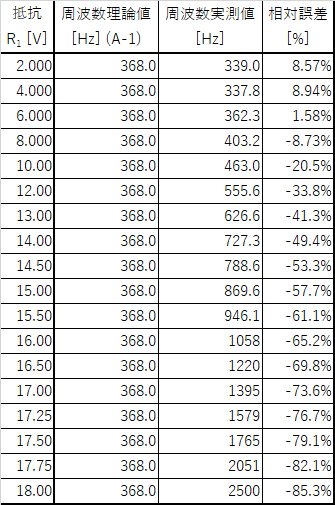
この結果を見ると，発振周波数は理論式と合わない領域が多く，しかも抵抗$R_1$に依存していることがわかります．抵抗$R_1$が$R_2$に近づくにつれどんどん周波数が高くなっていますね．ちなみに$R_1$をこれ以上大きくすると発振が止まってしまいました．

なぜ理論値と実測値が合わないのか

• Tr.2がON状態の時のベース - エミッタ間電圧 $V_{\mathrm{BE2(ON)}}$ を無視したから
  • 一般的に$V_{\mathrm{BE(ON)}}$は$0.7, \mathrm{[V]}$前後と低めですが(2SC1815の場合)，電源電圧$V_\mathrm{cc}$が低くなってくると影響ありそうです．
• コレクタ - エミッタ間飽和電圧$V_\mathrm{CE(SAT)}$を無視したから
  • これはトランジスタが完全にONになっても残ってしまう電圧で，一般的に$0.05, \mathrm{[V]}$前後と非常に小さいですが(2SC1815の場合)，影響がある可能性があります．
• Tr.がOFFからONになるために必要な $V_{\mathrm{BE}} , ( \equiv V_{\mathrm{th}} )$ を$0$として計算したから
  • 実験してみるとわかるのですが，この電圧は$0$ではなく，$V_{\mathrm{BE(ON)}}$よりも少しだけ低い値になります．これも影響してくるかもしれません．
• $t=0$になるまでに，電圧$V_{\mathrm{c1}}$が$V_{\mathrm{cc}}$になるまで十分に充電されると勝手に仮定したから
  • 図２で示している充電が遅かったり，充電できる時間（発振周期の半分）が短かったりすると，条件によっては十分に充電することができないかもしれません．

これを踏まえて改めて導出してみる

方針

感覚的に簡単に説明すると，考慮してなかったものを考慮したうえで，コンデンサの充電と放電による電圧のシーソーが釣り合うような$\mathrm{T}$と$V_\mathrm{c1(t=0)}$を探るというものです．
シーソーの具体的な説明は導出しながら説明します！！

1. $V_{\mathrm{BE2(ON)}}$や$V_{\mathrm{th}}, V_\mathrm{CE(SAT)}$を考慮する．
2. $V_\mathrm{c1(t=0)}$を$V_\mathrm{cc}$と決めつけず，未知数として計算する．
   3. 簡易式を求めた時と同様に，図３の放電経路の回路方程式から$V_\mathrm{c1(t=0)}^A(T)$を求めます．（シーソーの片方）
   4. これまでとは異なり，図２の充電経路の回路方程式から$V_\mathrm{c1(t=0)}^B(T)$を求めます．（シーソーのもう片方）
   5. 最後に$V_\mathrm{c1(t=0)}^A = V_\mathrm{c1(t=0)}^B$とすることで発振周期$\mathrm{T}$が求められる方程式が得られます！！（シーソーを釣り合わせる）

過程

※式の変形過程は簡易式とほとんど一緒なので，どんどん省略します．必要な場合は簡易式の過程を参照してください．

###放電経路の回路方程式
回路方程式は簡易式に$V_\mathrm{CE(SAT)}$を考慮することで，

R_2 \frac{dq(t)}{dt}+ \frac{1}{C}q(t)= V_\mathrm{cc}- V_\mathrm{CE(SAT)} \tag{2.1}

という微分方程式になります．($\because i= \frac{dq}{dt}$)
初期条件は，$-q(t=0)$(コンデンサの初期電荷量)を$CV_\mathrm{cc}$と決めつけず，

-q(t=0)= CV_\mathrm{C1(t=0)}^A \tag{2.2}

とします．初期条件にマイナスがついてるのは回路方程式の経路の影響です．

###放電経路の微分方程式を解く
$\mathcal{L}[q(t)]=\mathrm{Q}(s)$ としてラプラス変換して変形すると，

\mathrm{Q}(s)= \frac{C\left(V_\mathrm{cc}-V_\mathrm{CE(SAT)}\right)}{s}- \frac{C\left(V_\mathrm{cc}-V_\mathrm{CE(SAT)}+V_\mathrm{c1(t=0)}^A\right)}{s+\frac{1}{CR_2}} \tag{2.3}

となります．これを逆ラプラス変換することで，

q(t)= C \left(V_\mathrm{cc}-V_\mathrm{CE(SAT)}\right)- C\left(V_\mathrm{cc}-V_\mathrm{CE(SAT)}+V_\mathrm{c1(t=0)}^A\right)\exp{\left( -\frac{1}{CR_2}t \right)}

\begin{align}
V_\mathrm{BE2(t,V_\mathrm{c1(t=0)})}&= V_\mathrm{CE(SAT)}- \left\{ -\frac{1}{C}q(t) \right\} \\
&= V_\mathrm{cc}- \left(V_\mathrm{cc}-V_\mathrm{CE(SAT)}+V_\mathrm{c1(t=0)}^A\right)\exp{\left( -\frac{1}{CR_2}t \right)}  \tag{2.4}
\end{align}

となり，$V_\mathrm{BE2(t,V_\mathrm{c1(t=0)})}$が得られました．

###シーソーの放電経路側を求める
ここで，先ほどとは異なりTr.2がONになる条件として，$V_\mathrm{BE2(t,V_\mathrm{c1(t=0)})}\geq 0$ではなく,$V_\mathrm{BE2(t,V_\mathrm{c1(t=0)})}\geq V_{\mathrm{th}}$を使います．

$(2.3)$の$V_\mathrm{BE2(t,V_\mathrm{c1(t=0)})}$に$V_{\mathrm{th}}$を代入して変形し，$\mathrm{T=2T'}$を用いれば，

V_\mathrm{c1(t=0)}^A(\mathrm{T})= (V_\mathrm{cc}-V_{\mathrm{th}}) \left\{ \exp{\left( \frac{1}{2CR_2}\mathrm{T} \right)} - 1 \right\} - V_{\mathrm{th}}+V_\mathrm{CE(SAT)} \tag{B-1[のひとつ]}

と求まりました！
この式の物理的意味は，周期をTにしたければ，充電経路でコンデンサの電圧を↑にしてから引き渡してね！みたいな感じです．

##充電経路の回路方程式
今度は簡易式の導出では見なかったことにした図２の充電経路について考えてみます．

放電経路の時と異なる時間を基準にしたいので，$\mathrm{Tr_1}$がON状態からOFF状態に，$\mathrm{Tr_2}$がOFF状態からON状態に変化した瞬間を$t'=0 , \mathrm{[sec]}$とします．

充電経路について回路方程式を立てると，

R_1i_1+ \frac{1}{C} \int i_1 \, dt'+ V_\mathrm{BE2(ON)} = V_\mathrm{cc} \\
V_\mathrm{c1(t)}= \frac{1}{C} \int i_1 \, dt'

より，

CR_1 \frac{dV_\mathrm{c1(t')}}{dt'}+ V_\mathrm{c1(t')}= V_\mathrm{cc}- V_\mathrm{BE2(ON)} \tag{2.5}

という微分方程式になります．
初期条件は

V_\mathrm{c1(t'=0)}^B= V_\mathrm{CE(SAT)}-V_\mathrm{th} \tag{2.6}

です．（これは放電から充電に切り替わった瞬間のコンデンサの電圧です）

###充電経路の微分方程式を解く
$\mathcal{L}[V_\mathrm{c1(t')}]=Y(s)$としてラプラス変換して変形すると，

Y(s)= \frac{V_\mathrm{cc}- V_\mathrm{BE2(ON)}}{s}- \frac{V_\mathrm{cc}- V_\mathrm{BE2(ON)}+ V_\mathrm{th}-V_\mathrm{CE(SAT)} }{s+\frac{1}{CR_1}} \tag{2.7}

となります．（簡易式では$V_\mathrm{cc}$と決めつけたやつです）これを逆ラプラス変換して変形することで，

V_\mathrm{c1(t=0)}^B\mathrm{(T)}= \left( V_\mathrm{cc}- V_\mathrm{BE2(ON)}+ V_\mathrm{th}-V_\mathrm{CE(SAT)} \right) \left\{ 1- \exp{\left( -\frac{1}{CR_1}\mathrm{t'} \right)} \right\}- V_\mathrm{th}+V_\mathrm{CE(SAT)} \tag{2.8}

が得られました．

###シーソーの充電経路側を求める
$t'=\mathrm{T'}$の時にTr.のON,OFFが反転し，その時$t=0$なので，充電側のシーソーの式は，

V_\mathrm{c1(t=0)}^B(\mathrm T)= \left( V_\mathrm{cc}- V_\mathrm{BE2(ON)}+ V_\mathrm{th}-V_\mathrm{CE(SAT)} \right) \left\{ 1- \exp{\left( -\frac{1}{2CR_1}\mathrm{T} \right)} \right\}- V_\mathrm{th}+V_\mathrm{CE(SAT)} \tag{B-1[のひとつ]}

と求まりました！
この値の物理的意味は，周期をTにしてくれたら，コンデンサの電圧を↑まで充電してあげるよ！みたいな感じです．

##理論式を完成させる
最終的に，これまで求めた方程式を用いて以下の連立方程式がたてられます．

\begin{align} \left\{ \begin{array}{lll}
V^\mathrm{A}_\mathrm{c1(t=0)}&= (V_\mathrm{cc}-V_{\mathrm{th}}) \left\{ \exp{\left( \frac{1}{2CR_2}\mathrm{T} \right)} - 1 \right\} - V_{\mathrm{th}}+V_\mathrm{CE(SAT)} \tag{B-1} \\
V^\mathrm{B}_\mathrm{c1(t=0)}&= \left( V_\mathrm{cc}- V_\mathrm{BE2(ON)}+ V_\mathrm{th}-V_\mathrm{CE(SAT)} \right) \left\{ 1- \exp{\left( -\frac{1}{2CR_1}\mathrm{T} \right)} \right\}- V_\mathrm{th}+V_\mathrm{CE(SAT)} \\
V^\mathrm{A}_\mathrm{c1(t=0)}&= V^\mathrm{B}_\mathrm{c1(t=0)}
\end{array} \right. \end{align}

これをTで解けば発振周期が求まり，その逆数を求めることで発振周波数が求まります！
解析解が存在しないので，プログラムを書いて計算させることで求めることになります．
また，この連立方程式がシーソーに相当します．

##簡単化してみる
正直この方程式を解くのは面倒なので，パラメータに条件を付けて簡単化してみます．
$V^\mathrm{B}_\mathrm{c1(t=0)}$は充電回路側に関する辺ですが，

\exp{\left( -\frac{1}{2CR_1}\mathrm{T} \right)} \simeq 0

を満たすことができればコンデンサは十分に充電され，

V_\mathrm{c1(t=0)}= V_\mathrm{cc}- V_\mathrm{BE2(ON)}

となることがわかります．これを$V^\mathrm{A}_\mathrm{c1(t=0)}$に代入して計算すると，

f_\mathrm{osc} \fallingdotseq \left( 2CR_2 \ln{\frac{2V_\mathrm{cc}- V_\mathrm{BE2(ON)}-V_\mathrm{CE(SAT)} }{V_\mathrm{cc}- V_\mathrm{th}}} \right)^{-1} \, \mathrm{[Hz]} \tag{C-1}

\mathrm{T} \fallingdotseq 2CR_2 \ln{\frac{2V_\mathrm{cc}- V_\mathrm{BE2(ON)}-V_\mathrm{CE(SAT)}}{V_\mathrm{cc}- V_\mathrm{th}}} \, \mathrm{[sec]} \tag{C-2}

となり，より厳密な発振周波数を求めることができました！
但し，これには条件が存在し，$R_2 >> R_1$とする必要があります．

プログラム

詳細式(B-1)から発信周波数を求めるC++プログラムの例です．今回はニュートン法を用いています．
本プログラムでは例として抵抗$R_1$を可変パラメータにしているので，他のパラメータを可変にしたい場合は各自で変更してください．

#include <cmath>
#include <stdio.h>

// 式(C-2) を用いた発振周期の計算. ニュートン法の初期周期の決定に使用する.
double calc_t_c_2(double vcc, double vth, double vcesat, double vbeon, double c, double r2) {
    return 2 * c * r2 * std::log((2 * vcc - vbeon - vcesat) / (vcc - vth));
}

// V_{c1}^{A}を計算.
double calc_vc1_a(double vcc, double vth, double vcesat, double c, double r2, double t) {
    return (vcc - vth) * (std::exp(1 / (2 * c * r2) * t) - 1) - vth - vcesat;
}

// V_{c1}^{B}を計算.
double calc_vc1_b(double vcc, double vth, double vcesat, double vbeon, double c, double r1, double t) {
    return (vcc - vbeon + vth - vcesat) * (1 - std::exp(-1 / (2 * c * r1) * t)) - vth - vcesat;
}

// V_{c1}^{A}の微分を計算.
double calc_differential_vc1_a(double vcc, double vth, double c, double r2, double t) {
    return (vcc - vth) / (2 * c * r2) * std::exp(1 / (2 * c * r2) * t);
}

// V_{c1}^{B}の微分を計算.
double calc_differential_vc1_b(double vcc, double vth, double vcesat, double vbeon, double c, double r1, double t) {
    return (vcc - vbeon + vth - vcesat) / (2 * c * r1) * std::exp(-1 / (2 * c * r1) * t);
}

int main()
{
    double vcc = 8.0;       // 電源電圧 [V].
    double r2 = 19.6e3;     // 抵抗R2 [ohm].
    double c = 0.1e-6;      // コンデンサのキャパシタンス [F].
    double vth = 0.68;      // V_{th} [V].
    double vbeon = 0.80;    // V_{BE(ON)} [V].
    double vcesat = 0.10;   // V_{CE(SAT)} [V].
    double eps = 1e-9;      // 等しいとみなす差の最大値.
    int ite_max = 300;      // ニュートン法における最大の繰り返し回数.
    double eta = 0.6;       // 機械学習における学習率てきなやつ.


    for (int k = 1; k <= 18; k++) {
        double r1 = 1.0e3 * k; // 可変パラメータ 抵抗R1 [ohm].
        printf("r1 = %4.1f [kohm] : ", r1 / 1000);

        double t = calc_t_c_2(vcc, vth, vcesat, vbeon, c, r2); // 一番最初の探索位置.
        int ite = 0; // 更新の回数.

        while (1) {
            ite++;
            double vc1_a = calc_vc1_a(vcc, vth, vcesat, c, r2, t); // V_{c1}^{A}を計算.
            double vc1_b = calc_vc1_b(vcc, vth, vcesat, vbeon, c, r1, t);// V_{c1}^{B}を計算.
            double sa = vc1_a - vc1_b;

            if (std::abs(sa) < eps) { // 解が見つかった.
                printf("freq = %7.2f [Hz] (ite = %2d)\n", 1 / t, ite);
                break;
            }
            else if (ite > ite_max) { // 解が見つからないときは打ち切る.
                printf("Not Found\n");
                break;
            }

            double differential_vc1_a = calc_differential_vc1_a(vcc, vth, c, r2, t); // V_{c1}^{A}の微分を計算.
            double differential_vc1_b = calc_differential_vc1_b(vcc, vth, vcesat, vbeon, c, r1, t); // V_{c1}^{B}の微分を計算.
            double sa2 = differential_vc1_a - differential_vc1_b; // 微分した結果の差を計算.
            t = t - (sa / sa2) * eta; // ニュートン法に基づいて次の周期を決定.
        }
    }
}

#検証
##(C-1)の検証
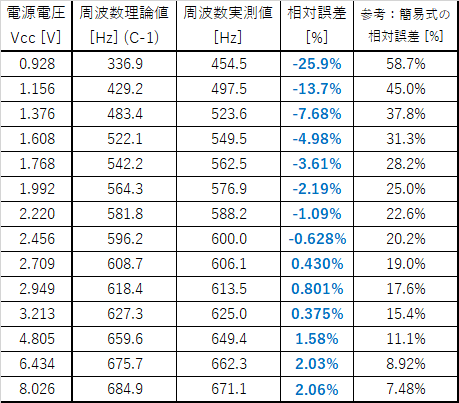
上のほうで実測した，電源電圧を変化させたときの発振周波数のグラフに，式(C-1)から求めた理論式を追加してみたのが図６です．データを表３に示します．
今回は$V_\mathrm{th}=0.70, \mathrm{[V]}$, $V_\mathrm{BE2(ON)}=0.80, \mathrm{[V]}, V_\mathrm{CE(SAT)}=0.05, \mathrm{[V]}$として計算しています．

その結果，求めた詳細式(C-1)は簡易式(A-1)よりも実測値に近い値が得られることがわかります．

図６．電源電圧を変化させてみた時の発振周波数

表３．電源電圧を変化させてみた時の発振周波数（データ）

##(B-1)の検証
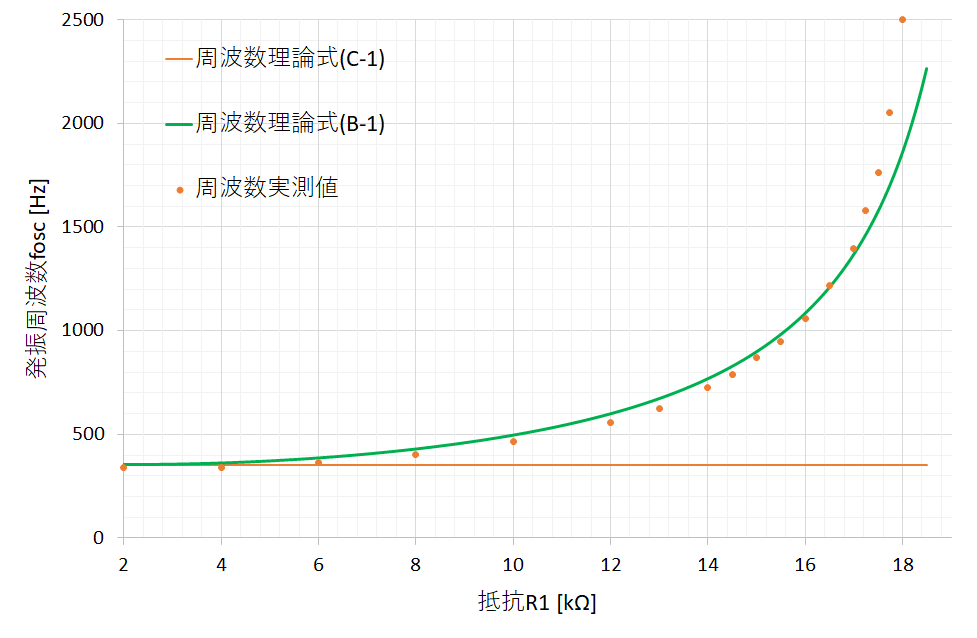
上のほうで実測した，抵抗$R_1$を変化させたときの発振周波数のグラフから簡易式(A-1)を削除して，その後式(C-1)と(B-1)から求めた理論式を追加してみたのが図７です．データを表４に示します．
今回は$V_\mathrm{th}=0.68, \mathrm{[V]}$, $V_\mathrm{BE2(ON)}=0.80, \mathrm{[V]}, V_\mathrm{CE(SAT)}=0.10, \mathrm{[V]}$として計算しています．

その結果，詳細式(B-1)では，抵抗$R_1$が大きいときでも実測値にかなり近い値をとることができることがわかります．また，$R_1$が十分に小さいときは詳細式の簡易版(C-1)でもいい結果が得られました．

また，$R_1$が大きい所では誤差が大きくなりますが，これはパラメータ値($V_\mathrm{th}, V_\mathrm{BE2(ON)}$など)の測定誤差や，まだ考慮してない何かが存在することによるものだと考えています．（確証がない）
ただ，通常$R_1$は$R_2$と比較して十分に小さい領域で発振させるので，あまり気にする必要はないです．

図７．抵抗$R_1$を変化させてみた時の発振周波数

表４．抵抗$R_1$を変化させてみた時の発振周波数（データ）

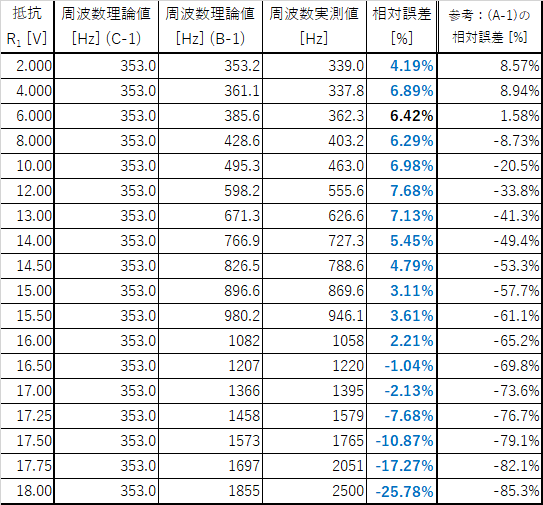
まとめ

$R_2>>R_1$を満たす場合，式$(C-1)$を用いることによって，無安定マルチバイブレータのより正確な発振周波数を求めることができます．
$R_2>>R_1$を満たさない回路の場合は式$(B-1)$を$\mathrm{T}$について解けば求められます．

ただ，それでも誤差は出てくるので回路を組んでから調整するのは必須だと言えそうです．

おまけ

この記事を書くために実験した時の風景や使用したオシロスコープの画像を発掘したので載せておきます．
可変電圧源の代わりにショットキーバリアダイオードの電圧降下を利用したり，アナログオシロをヤフオクで2000円で落札して購入したりと，当時の金欠ぶりを思い出しました...

図８．実験風景

図９．使用したオシロスコープ