1. はじめに
1-1. 本記事の概要と目標
今回はGRU/LSTMで将来の電力需要の予測を行います。
前回の記事を踏まえた内容となっておりますので、
まだご覧頂いていない方はこちらを先にご覧下さい。
前回行ったのは東京電力の公開する電気消費量の実績データにて、
RNN/GRU/LSTMの予測精度の比較、及び前処理による比較です。
前回の予測では特徴量に "月", "日" ,"時", "曜日" に加え、
"天気", "気温", "降水量", "湿度" の8つを用いていました。
しかし完全に未知である将来の予測においては、
上記のような 気象情報も未知のデータになってしまうため、
前回のモデルでは完全に未知な将来の予測ができません でした。
今回の記事における分析のテーマは、
上記の課題を解決するための方法を検討することとなります。
1-2. 課題の整理
まずは前回の課題を整理していきます。
前回の課題としてポイントになるのは、
「特徴量に未来の気象情報が含まれていること」 です。
これに対して考えられる対策として、以下の3つを軸に考えます。
・手元のデータの末尾に対する予測を入力とするループ予測
・そもそも特徴量に気象情報を用いないモデル構築
・一部の特徴量を別のモデルで予測する2重予測
以下、各手法について考えたことをまとめます。
1-2-1. ループ予測について
まず1つ目のループ型の予測についてです。
モデルの構築には以下のページを参考にしていますので、
作成のイメージなどはこちらをご確認下さい。
例として、4月末日のデータ(説明8:目的1)を入力とした場合、
出力も同様の形(説明8:目的1)で5月1日のデータを出力します。
そのうち説明変数のみを取り出してまた入力として再利用することで、
どんな期間でも予測した値を出力することが可能になります。
その際の目的変数を別で格納することで、予測値の確認も可能です。
しかしこの手法の場合、"天気"の予測が非常に難しく、
それに伴い"湿度", "降水量"の予測も困難 となります。
今回はまず最初にそちらを実装していきますが、
あくまでも手法の一つとして精度を確認する目的で行います。
1-2-2. 気象情報を用いないモデル構築について
次に2つ目は 気象情報を用いずに行う予測 です。
言い換えると、日時のみを説明変数にして行う電気需要予測です。
やはり気象情報自体は予測が困難なものなので、
初めからそれを無しにして直接予測を行おうという考えです。
しかし 純粋に様々な情報を失ったモデルになってしまう ため、
精度が大幅に下がってしまうことは予想できると思います。
こちらも比較の対象として試験的に実装していきます。
1-2-3. 説明変数を別モデルで予測する2重予測について
次に考えたのが、辛うじて 予測ができそうな"気温"のみ
別で構築したモデルにて予測を行い、それを特徴量とする 手法です。
こちらは気温の予測に対する精度も結果に影響するため、
非常に手間は掛かりそうですが、最終的な精度は期待できそうです。
またこの手法に加えて、"気温"が予測可能だと考える場合、
日時と気温の5つを説明変数にしてループ予測ができそう なので、
こちらも併せて実装していきます。
2. 実装
使用するデータセットは前回と同様です。
df = pd.read_csv("./data/df_ver1.csv")
df
今回の学習/予測に使うモデルとしては、
前回記事にて 精度が安定し、学習も早かったGRU を使います。
unit=256, dropout=0.2のスタックモデルです。
またモデル構築の際にコードを記載します。
そして検討する手法についてですが、
上記項目の内容を踏まえ、以下の4つで行います。
1.全ての説明変数(8個)に対してループ予測
2.目的変数のみを直接予測
3.気温を予測するモデルを別に構築
4.日時と気温の説明変数(5個)に対してループ予測
2-1. 全ての説明変数(8個)に対してループ予測
まずは前回の内容を引き継いだ全ての説明変数に対して、
手元のデータの最後の時刻に対する予測を入力として、
繰り返し予測を行う手法 について実装していきます。
2-1-1. 前処理
import pandas as pd
import datetime as dt
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_percentage_error
from keras.models import Sequential
from keras.layers import Dense, LSTM, SimpleRNN, GRU
from keras.layers import Dropout
from tensorflow.keras.callbacks import EarlyStopping
#使用しない特徴量を落として、目的変数の"kw"を後ろに移動
kw = df["kw"]
df = df.iloc[:,4:]
df["kw"] = kw
#処理を軽くするためarray型に
data = df.values
#参照する時刻を6件に設定
timesteps = 6
#全体の約17%をtestデータとして分割
#2021/4/30 23時のデータまでをtrainに
train_size = 29183
train = data[:train_size, :]
#テストデータの最初の予測で5月1日0時を予測するため
test = data[train_size-timesteps:, :]
ここまでで必要なモジュールのインポート、
訓練データとテストデータの分割までを行っています。
今回は4月末までのデータが手元にあるという想定のため、
テストデータでは最初の予測する値が5月1日の0時になるように
test = data[train_size-timesteps:, :]としています。
from sklearn.preprocessing import MinMaxScaler
#スケーリング
mms = MinMaxScaler()
train = mms.fit_transform(train)
test = mms.transform(test)
#特徴量全てについて予測するためデータ全てをyにする
x_train = train[:, :-1]
y_train = train[:, :]
x_test = test[:, :-1]
y_test = test[:, :]
#trainについてデータ変換
data_x = []
for i in range(x_train.shape[0]-timesteps):
timedelta_x = []
for j in range(x_train.shape[1]):
timedelta_x.append(x_train[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_train = np.array(data_x)
y_train = y_train[6:, :]
#testについてデータ変換
data_x = []
for i in range(x_test.shape[0]-timesteps):
timedelta_x = []
for j in range(x_test.shape[1]):
timedelta_x.append(x_test[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_test = np.array(data_x)
y_test = y_test[6:, :]
x_train.shape, y_train.shape, x_test.shape, y_test.shape
ここで前回同様に訓練データを3次元に変換しています。
今回は全ての特徴量に対して予測を行うので、
y_train, y_testは特徴量全てを入れています。
この時点での各データのshapeは以下の通りです。
((29177, 6, 8), (29177, 9), (5880, 6, 8), (5880, 9))
2-1-2. 予測
%%time
neuron = 256
actfunc = "tanh"
dropout = 0.2
epochs = 300
model = Sequential()
model.add(GRU(neuron, activation=actfunc, batch_input_shape=(None, timesteps, x_train.shape[2]), return_sequences=True))
model.add(Dropout(dropout))
model.add(GRU(neuron, activation="relu"))
modeladd(Dropout(dropout))
model.add(Dense(y_train.shape[1], activation="linear"))
model.compile(loss="mean_squared_error", optimizer="adam")
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0.0, patience=5)
history = model.fit(x_train, y_train, batch_size=128, epochs=epochs, validation_split=0.2, callbacks=[early_stopping])
モデルは前述の通りGRUのスタックモデルです。
最後の出力はy_train.shape[1]としています。
学習の過程をプロットします。
plt.figure(figsize=(15,8))
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='valid Loss')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epochs')
plt.legend(loc='upper right')
plt.show()
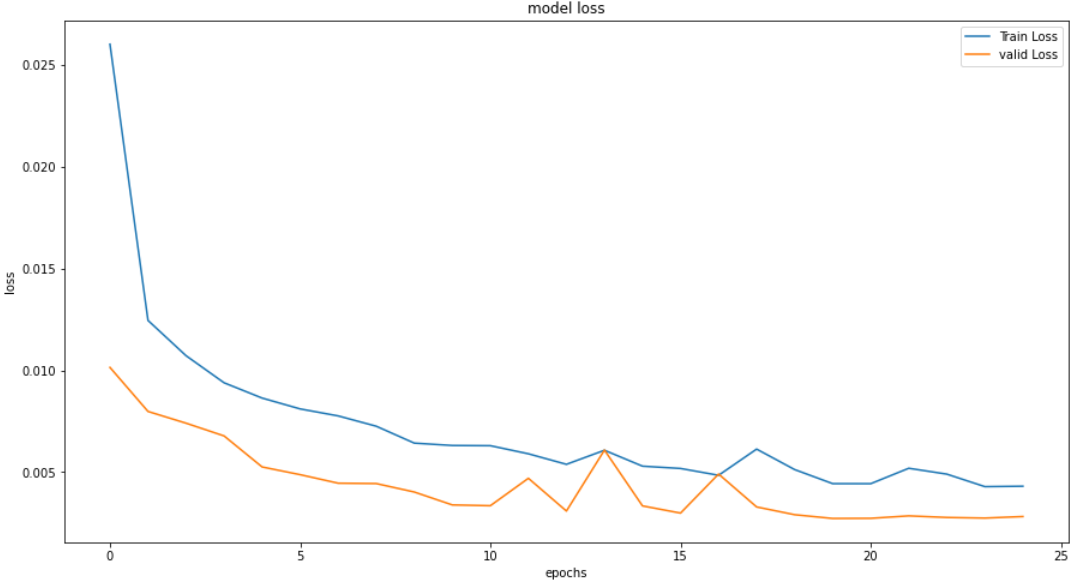
25エポックで学習時間は1,488秒でした。
実際に最初の予測を確認してみます。
#1個目の予測データと正解(2行目)を比較
res = model.predict(x_test[0].reshape(1,timesteps,8))
res = np.concatenate([res, y_test[0].reshape(1,9)], 0)
pd.DataFrame(mms.inverse_transform(res))

上の行が予測した値で、下の行が正解の値です。
まさかの4月25日1時頃にタイムスリップしていました。
この先の予測がとても不安ではありますが、
これを繰り返して1か月先の5月末までを予測してみます。
%%time
input_data = x_test[0]
y_test_pred = []
n_iter = 744 #翌月1か月分を予測(24*31)
for i in range(n_iter):
pred = model.predict(input_data.reshape(1,6,8), verbose=0) #最初は5/1 00:00を予測
pred[:,:4] = x_test[i+1][-1, :4] #日時と曜日データを正しいデータに置き換え
next_input = np.concatenate([input_data, pred[:,:-1].reshape(1,8)])[1:,:] #次の入力データを定義
input_data = next_input
y_test_pred.append(pred) #予測を結果として保存
y_test_pred = np.array(y_test_pred).reshape(n_iter, y_test.shape[1])
先ほどのタイムスリップの実例でも分かったように、
予測値では日時のデータですら正しく出力されていません。
そのため 前の出力を新しい入力として受け取る際に、
正しい日時のデータと入れ替える 作業を挟んでいます。
(気象情報とは違い日時のデータは予め作成できるため)
ではこちらも前回と同様に精度を出力してみます。
y_test_pred = mms.inverse_transform(y_test_pred)[:, -1]
y_t = mms.inverse_transform(y_test[:n_iter])[:, -1]
RMSE = np.sqrt(mean_squared_error(y_t, y_test_pred))
MAE = mean_absolute_error(y_t, y_test_pred)
MAPE = mean_absolute_percentage_error(y_t, y_test_pred)
# 指標出力
print('RMSE:')
print(RMSE)
print('MAE:')
print(MAE)
print('MAPE:')
print(MAPE)
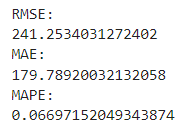
もっととんでもない結果になるかとも思いましたが、
説明変数の"kw"は「平均:3,238、標準偏差:667」 であるため、
思っていたほど悪くない数値でした。
最後に1か月分の予測をプロットしておきます。

少し見づらいかも知れませんが、黄色が予測値です。
中盤においてはそれほど悪くない精度のように見えます。
2-2. 目的変数のみを直接予測
次に行うのは目的変数のみ予測するモデル構築です。
予測が困難な気象情報は取り扱わない手法 となっています。
2-2-1. 前処理
kw = df["kw"]
df = df.iloc[:,4:8]
df["kw"] = kw
data = df.values
timesteps = 6
train_size = 29183
train = data[:train_size, :]
test = data[train_size-timesteps:, :]
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
train = mms.fit_transform(train)
test = mms.transform(test)
x_train = train[:, :-1]
y_train = train[:, -1].reshape(-1,1)
x_test = test[:, :-1]
y_test = test[:, -1].reshape(-1,1)
data_x = []
for i in range(x_train.shape[0]-timesteps):
timedelta_x = []
for j in range(x_train.shape[1]):
timedelta_x.append(x_train[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_train = np.array(data_x)
y_train = y_train[6:]
data_x = []
for i in range(x_test.shape[0]-timesteps):
timedelta_x = []
for j in range(x_test.shape[1]):
timedelta_x.append(x_test[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_test = np.array(data_x)
y_test = y_test[6:]
x_train.shape, y_train.shape, x_test.shape, y_test.shape
ここの処理は先ほどとほとんど同じで、
この時点でのshapeは以下のようになっています。
((29177, 6, 4), (29177, 1), (5880, 6, 4), (5880, 1))
変更点としては序盤にカラムを指定したdf = df.iloc[:,4:8]と、
終盤のy_train = y_train[6:]の辺りかと思います。
2-2-2. 予測
上記データで学習を行い、精度を見ていきます。
モデルの構築は先ほどと同じなので割愛します。

学習は19エポックで時間は436秒でした。
pred = model.predict(x_test)
pred = np.concatenate([test[timesteps:, :-1], pred], 1)
y_test_pred = mms.inverse_transform(pred)[:744, -1]
y_t = np.concatenate([test[timesteps:, :-1], y_test], 1)
y_t = mms.inverse_transform(y_t)[:744, -1]
RMSE = np.sqrt(mean_squared_error(y_t, y_test_pred))
MAE = mean_absolute_error(y_t, y_test_pred)
MAPE = mean_absolute_percentage_error(y_t, y_test_pred)
# 指標出力
print('RMSE:')
print(RMSE)
print('MAE:')
print(MAE)
print('MAPE:')
print(MAPE)

RMSEは134まで大幅に改善した結果となりました。
情報が少なくても周期性のあるデータは案外予測できるようです。
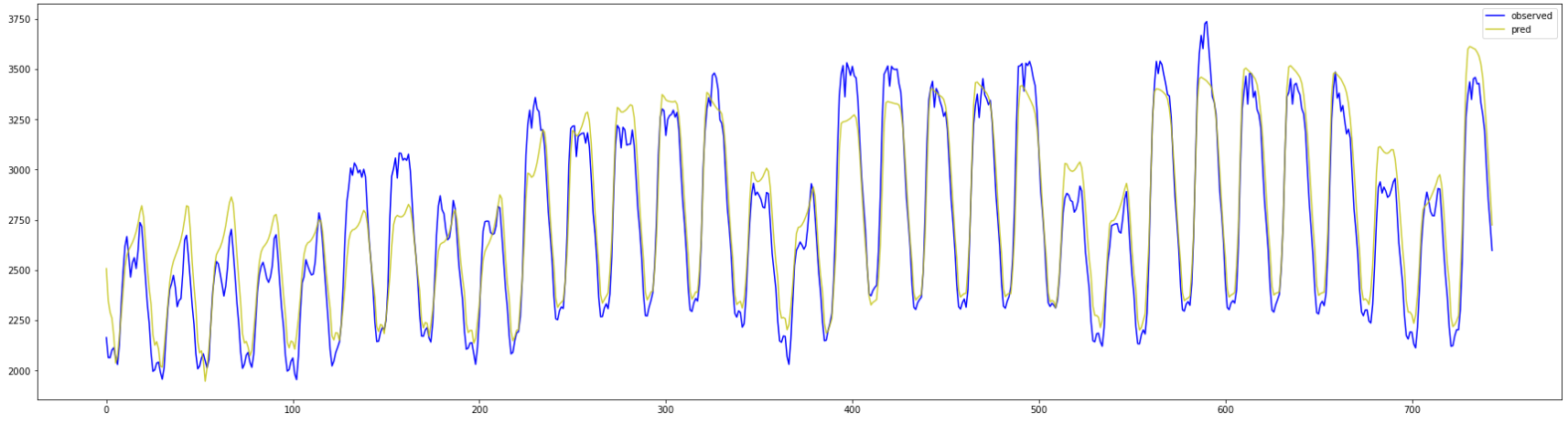
確実に先ほどのデータよりはうまく予測もできています。
2-3. 気温を予測するモデルを別に構築
つぎは 気温のみ別のモデルで一度予測したのち、
その予測した値を説明変数として予測を行う手法 です。
2-3-1. 前処理
kw = df["kw"]
df = df.iloc[:,4:9]
df["kw"] = kw
data = df.values
timesteps = 6
train_size = 29183
train = data[:train_size, :]
test = data[train_size-timesteps:, :]
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
train = mms.fit_transform(train)
test = mms.transform(test)
x_train = train[:, :-1]
y_train = train[:, -1].reshape(-1,1)
x_test = test[:, :-1]
y_test = test[:, -1].reshape(-1,1)
data_x = []
for i in range(x_train.shape[0]-timesteps):
timedelta_x = []
for j in range(x_train.shape[1]):
timedelta_x.append(x_train[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_train = np.array(data_x)
y_train = y_train[6:]
data_x = []
for i in range(x_test.shape[0]-timesteps):
timedelta_x = []
for j in range(x_test.shape[1]):
timedelta_x.append(x_test[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_test = np.array(data_x)
y_test = y_test[6:]
#気温を予測するためのデータセット
x_train_temp = x_train[:, :, :-1]
y_train_temp = train[6:, -2].reshape(-1,1)
x_test_temp = x_test[:, :, :-1]
y_test_temp = test[6:, -2].reshape(-1,1)
#以下を出力して確認
x_train.shape, y_train.shape, x_test.shape, y_test.shape
x_train_temp.shape, y_train_temp.shape, x_test_temp.shape, y_test_temp.shape
今回も前処理はほとんど同じになりますが、
df = df.iloc[:,4:9]で特徴量に気温を入れて、
最後に別でデータセットを作成している点が異なります。
このときのデータのshapeは以下のようになっています。
下の行が気温を予測するためのデータセットです。
((29177, 6, 5), (29177, 1), (5880, 6, 5), (5880, 1))
((29177, 6, 4), (29177, 1), (5880, 6, 4), (5880, 1))
2-3-2. メインのモデルで学習
%%time
neuron = 256
actfunc = "tanh"
dropout = 0.2
epochs = 300
model = Sequential()
model.add(GRU(neuron, activation=actfunc, batch_input_shape=(None, timesteps, x_train.shape[2]), return_sequences=True))
model.add(Dropout(dropout))
model.add(GRU(neuron, activation="relu"))
model.add(Dropout(dropout))
model.add(Dense(y_train.shape[1], activation="linear"))
model.compile(loss="mean_squared_error", optimizer="adam")
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0.0, patience=5)
history = model.fit(x_train, y_train, batch_size=128, epochs=epochs, validation_split=0.2, callbacks=[early_stopping])
まずは"kw"を予測するためのメインモデルを学習します。
こちらのデータでも予測の経過を確認します。

学習は12エポックの278秒でした。
次に気温を予測するモデルを構築します。
%%time
neuron = 256
actfunc = "tanh"
dropout = 0.2
epochs = 300
model_temp = Sequential()
model_temp.add(GRU(neuron, activation=actfunc, batch_input_shape=(None, timesteps, x_train_temp.shape[2]), return_sequences=True))
model_temp.add(Dropout(dropout))
model_temp.add(GRU(neuron, activation="relu"))
model_temp.add(Dropout(dropout))
model_temp.add(Dense(y_train_temp.shape[1], activation="linear"))
model_temp.compile(loss="mean_squared_error", optimizer="adam")
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0.0, patience=5)
history_temp = model_temp.fit(x_train_temp, y_train_temp, batch_size=128, epochs=epochs, validation_split=0.2, callbacks=[early_stopping])
ではこのモデルで 翌1か月の気温を予測し、
データセットに再度変換してからメインモデルで予測 します。
データセットに変換する際に先頭6行の目的変数は除かれるため、
参照する行数を738行(744-timesteps行)に調整しています。
pred = model_temp.predict(x_test_temp)
pred = np.concatenate([test[timesteps:, :-2], pred], 1)
data_x = []
for i in range(pred.shape[0]-timesteps):
timedelta_x = []
for j in range(pred.shape[1]):
timedelta_x.append(pred[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_test_2 = np.array(data_x)
pred = model.predict(x_test_2)
pred = np.concatenate([test[timesteps*2:, :-1], pred], 1)
y_test_pred_2 = mms.inverse_transform(pred)[:738,-1]
y_t = np.concatenate([test[timesteps*2:, :-1], y_test[timesteps:, :]], 1)
y_t = mms.inverse_transform(y_t)[:738,-1]
RMSE_2 = np.sqrt(mean_squared_error(y_t, y_test_pred_2))
MAE_2 = mean_absolute_error(y_t, y_test_pred_2)
MAPE_2 = mean_absolute_percentage_error(y_t, y_test_pred_2)
# 指標出力
print('RMSE:')
print(RMSE_2)
print('MAE:')
print(MAE_2)
print('MAPE:')
print(MAPE_2)

最終的な結果は更に改善されており、
MAEについては100を切る 精度となりました。
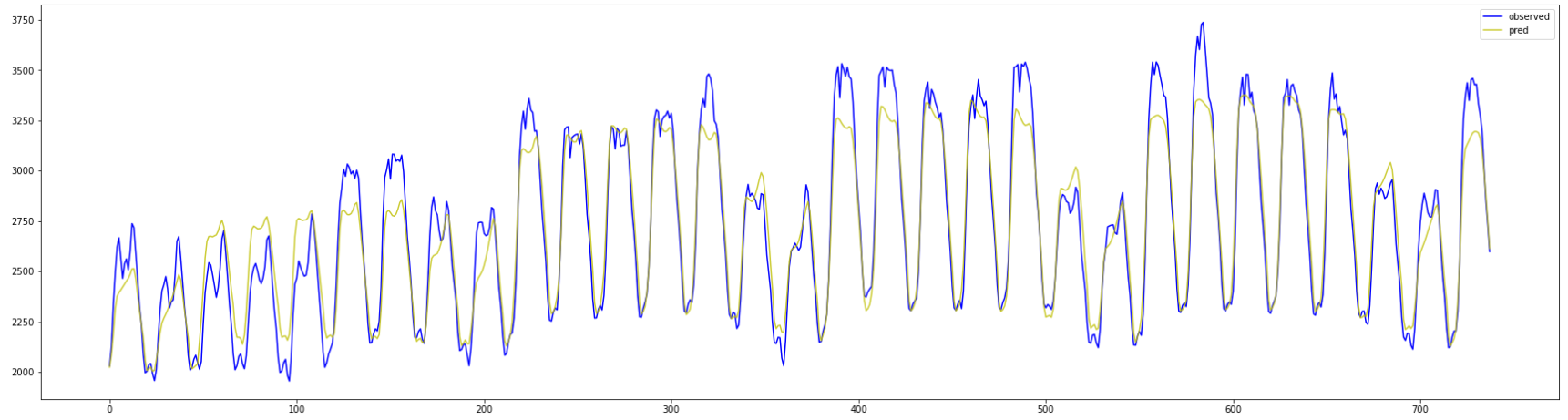
1か月分のプロットも、上手い具合に日毎の流れに沿っています。
2-4. 日時と気温を特徴量(5個)に対して繰り返し予測
最後は ループ予測の特徴量に日時と気温を用いる予測 です。
気温が予測可能ならこちらもある程度の精度は出そうです。
kw = df["kw"]
df = df.iloc[:,4:9]
df["kw"] = kw
data = df.values
timesteps = 6
train_size = 29183
train = data[:train_size, :]
test = data[train_size-timesteps:, :]
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler()
train = mms.fit_transform(train)
test = mms.transform(test)
x_train = train[:, :-1]
y_train = train[:, :]
x_test = test[:, :-1]
y_test = test[:, :]
data_x = []
for i in range(x_train.shape[0]-timesteps):
timedelta_x = []
for j in range(x_train.shape[1]):
timedelta_x.append(x_train[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_train = np.array(data_x)
y_train = y_train[6:, :]
data_x = []
for i in range(x_test.shape[0]-timesteps):
timedelta_x = []
for j in range(x_test.shape[1]):
timedelta_x.append(x_test[i:i+timesteps, j])
timedelta_x = np.array(timedelta_x)
timedelta_x = timedelta_x.transpose()
data_x.append(timedelta_x)
x_test = np.array(data_x)
y_test = y_test[6:, :]
x_train.shape, y_train.shape, x_test.shape, y_test.shape
こちらも前述のループ予測とほぼ同様ですが、
df = df.iloc[:,4:9]で気温を説明変数に含め、
y_train = train[:, :]のところで特徴全てを予測対象にしています。

エポック数は21回で学習時間は389秒でした。
#1個目の予測データと正解(2行目)を比較
res = model.predict(x_test[0].reshape(1,timesteps,5))
res = np.concatenate([res, y_test[0].reshape(1,6)], 0)
pd.DataFrame(mms.inverse_transform(res))
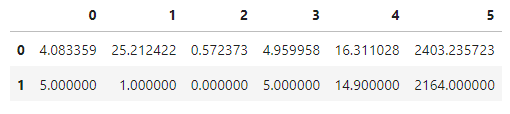
最初の予測と正解データを確認してみると、
やはり4月25日1時頃として予測されているようです。
%%time
input_data = x_test[0]
y_test_pred = []
n_iter = 744 #翌月1か月分を予測(24*31)
for i in range(n_iter):
pred = model.predict(input_data.reshape(1,timesteps,x_test.shape[2]), verbose=0) #最初は5/1 00:00を予測
pred[:,:4] = x_test[i+1][-1, :4] #日時と曜日データを正しいデータに置き換え
next_input = np.concatenate([input_data, pred[:,:-1].reshape(1,x_test.shape[2])])[1:,:] #次の入力データを定義
input_data = next_input
y_test_pred.append(pred) #予測データを結果として保存
y_test_pred = np.array(y_test_pred).reshape(n_iter, y_test.shape[1])
このモデルでも1か月分のデータについて予測を行います。
for文の中身は最初のモデルと全く同じです。
y_test_pred = mms.inverse_transform(y_test_pred)[:, -1]
y_t = mms.inverse_transform(y_test[:n_iter])[:, -1]
RMSE = np.sqrt(mean_squared_error(y_t, y_test_pred))
MAE = mean_absolute_error(y_t, y_test_pred)
MAPE = mean_absolute_percentage_error(y_t, y_test_pred)
# 指標出力
print('RMSE:')
print(RMSE)
print('MAE:')
print(MAE)
print('MAPE:')
print(MAPE)

結果はあまりよくありませんでした。
連続の予測だと少しずつズレが生じるのかも知れません。

所々上下の振れ幅がずれている様子が見て取れます。
やはり連続的な数値予測は少し難しそうですね。
3. 結果の確認
3-1. 前回の方法による予測精度
ここで比較のベンチマークの1つとして、
前回の方法で同期間を予測した際の結果を見ておきます。
この方法は本来分かるはずのない未来の気象情報を
特徴量に入れている非現実的な予測方法です。

精度はRMSEが144.85、MAEが93.09でした。
気温を別で予測したモデルと比較すると、
RMSEは悪化、MAEとMAPEは改善 されています。

上下の振れ幅でいくつか大きく外していますが、
全体的に精度の高い予測がされているように見えます。
やはり正確な気象情報があると予測の精度は上がるようです。
3-2. 結果の比較
以下に全モデルの結果を一覧で示します。
少し見づらいですが、黄色のプロットが予測値です。

未知の値を説明変数に用いる非現実的な手法を除き、
気温の予測値を用いるモデルの精度が最も良い 結果となりました。
時点で精度の良いモデルは気象情報を用いず、
直接目的変数である電力消費量を予測するモデルでした。
他のループ予測2つは精度があまり良くありませんでした。
予測を繰り返すうちに次第にズレが大きくなるためだと考えられます。
4. 考察と課題
4-1. 分析の考察
今回は主に4つのモデルについて比較検討を行いました。
結果的には "未知の特徴量を用いずに直接予測する"、
または "一部の予測可能な値を予測するモデルを別で構築する"、
などの手法による精度が良いという結果になりました。
予測値を次の入力値として受け取るループ予測については、
予測を繰り返すたびに精度のズレが重なるため、
期間が長ければ長いほど精度は悪化することが予想できます。
4-2. 今後の課題
今後の課題としては以下の4つが挙げられます。
・LSTMとの比較
・timesteps(参照する前期間)による比較
・湿度や降水量も予測するモデルを構築
・より長期間に対する予測を比較
実際の業務では年間の予算を試算するためなどに、
1年間や4半期の需要を予測するケースなどもあるかと思います。
その場合もやはり値を直接LSTMなどで予測したり、
一部特徴量を別モデルで予測する手法が良さそうです。
しかし今回扱った電気需要は季節性を持つ変動です。
リアルタイムに情報と値が変動する株価のようなものは、
値をループで予測するモデルの検討も必要かも知れません。
4-3. 所感
前回の記事の内容ではモデルの構築のみ経験しましたが、
今回は方法を変更して未知期間の予測を行いました。
正直なところ前回の記事の時点ではまだ理解が曖昧で、
コードを見返しても課題の多い内容だと感じました。
今回の記事もまだ理解の足りていないところがあるかと思います。
もし誤植を見つけた方がいればコメントお願いします。
4-4. さいごに
最後まで記事を読んで下さりありがとうございました。
ぜひお気軽にコメントなどよろしくお願い致します。
参考ページ