この記事は、正規分布の説明と利用方法を記載しています。
読者は、次の問題がわかる人を前提にしています。
Q.「平均60点で標準偏差15点の算数のテストがあったとき、偏差値60だった人は何点をとっていますか?」
A. 正解は「75点」
二項分布
成功確率 p の事象を n 回試行したときの成功回数 r の分布を r ~ B(n, p) と書く.
成功回数が r となる確率 Pr[r ] は,
n 回の試行で r 回成功する 場合の数が nCr 通りで, r 回成功し n-r 回失敗するので,
$$
\begin{align}
$P_r[r]={}_n C _r p^r (1-p)^{n-r}
\end{align}
$$
となる.また、確率分布の平均と分散は
$$
\begin{align}
\mbox{平均: } \bar{x} &= np & \\
\mbox{分散: } s^2 &= np(1 - p) & \\
\end{align}
$$
である.
例題
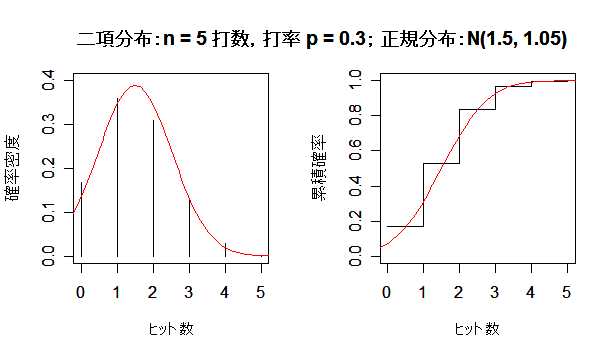
A 選手は 3 割バッターである.ある試合で 5 回打席に立ったときときのヒット数の分布を求める.
この場合,p=0.3,n=5である.
$$
\begin{align}
\mbox{5打数ノーヒットの確率:} & \mbox{ヒットが出ない確率は,1-0.3=0.7なので,求める確率は} & \\
P_r[0] &=0.7^5 &=0.16807\\
\mbox{5打数1安打の確率:}P_r[1] &= {}_5 C _1p(1-p)^4 & =5×0.3×0.7^4=1.5×0.2401 =0.36015 \\
\mbox{5打数2安打の確率:}P_r[2] &= {}_5 C _2 p^2(1-p)^3 & =(5×4)/(2×1)×0.3^2×0.7^3 =0.3087 \\
\mbox{5打数3安打の確率:}P_r[3] &= {}_5 C _3 p^3(1-p)^2 & =(5×4×3)/(3×2×1)×0.3^3×0.7^2=10×0.027×0.49 =0.1323 \\
\mbox{5打数4安打の確率:}P_r[4] &= {}_5 C _4 p^4(1-p) & =5×0.34×0.7=3.5×0.0081 =0.02835 \\
\mbox{5打数5安打の確率:} P_r[5] &= p^5 & =0.35 =0.00243 \\
\end{align}
$$
これより,ヒット数の分布は以下の表のように書ける.
| ヒット数 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 確率 | 0.16807 | 0.36015 | 0.3087 | 0.1323 | 0.02835 | 0.00243 |
の形で表現される.
このとき,確率分布の平均と分散は,
$$
\begin{align}
\mbox{平均: } \bar{x} &= x_1p_1 + x_2p_2 + \cdots + x_np_n = \sum_{i=1}^{n}{x_ip_i} & \\
\mbox{分散: } s^2 &= (x_1 - \bar{x})^2p_1 + (x_2 - \bar{x})^2p_2 + \cdots + (x_n - \bar{x})^2p_n = \sum_{i=1}^{n}(x_i - \bar{x})^2p_i
\end{align}
$$
と定義される.
これより,ヒット数の平均と分散は,
$$
\begin{align}
\mbox{平均: } \bar{x} &= 0\cdot0.16807+1\cdot0.36015+2\cdot0.3087+3\cdot0.1323+4\cdot0.02805+5\cdot0.00243 & \\ &= 1.5 \\
\mbox{分散: } s^2 &= (0-1.5)^2\cdot0.16807+(1-1.5)^2\cdot0.36015+(2-1.5)^2\cdot0.3087+(3-1.5)^2\cdot0.1323+(4-1.5)^2\cdot0.02805+(5-1.5)^2\cdot0.00243 & \\ &= 1.05
\end{align}
$$
と計算される.
実は,成功確率 p の事象を n 回行ったときの二項分布 B(n,p) の平均と分散は
$$
\begin{align}
\mbox{平均: } \bar{x} &= np & \\ &= 5\cdot0.3 & \\ &= 1.5 \\
\mbox{分散: } s^2 &= np(1 - p) & \\ &= 5\cdot0.3\cdot0.7 & \\ &= 1.05 \\
\end{align}
$$
となることがわかる.
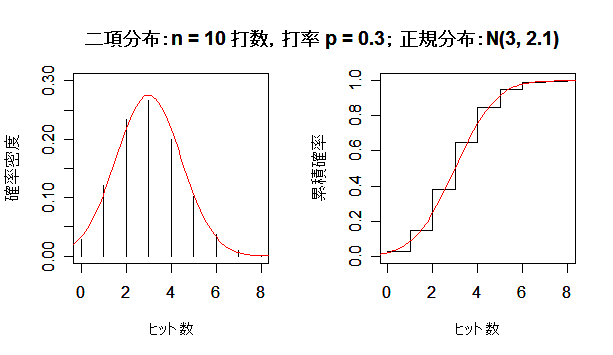
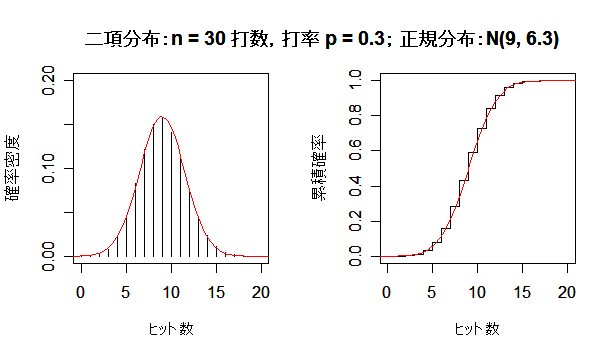
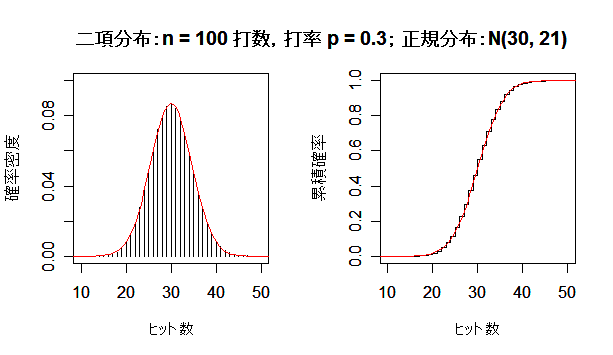
二項分布が正規分布に近づく様子
成功確率 p の二項分布は,試行回数 n を増やしていくと,平均 np,分散 np(1 - p) の正規分布 に近づく.左図が確率分布(密度)で,右図が累積分布である.
t分布
標本nが小さい(n<30)とき母集団を推定するときは、
t分布を用いて、自由度は n-1 として計算する
二項分布の応用
視聴率調査
問い①
ある番組の視聴率とは、無作為に抽出された世帯を標本として調査し、視聴率としている.
n 世帯を無作為に抽出して、視聴率の標準偏差を 1% 以下にするには、n は最低でもいくらでなければならないか?
解答
「抽出された n 世帯のうち、その番組を見ている世帯の数」を X
「抽出された n 世帯のうち、その番組を見ている世帯の割合」を X/n = p^ (ハット:推定値)
とする.
X は確率変数で二項分布B(n, p)に従うので、
X の平均は np
X の分散は np(1-p) となる.
このとき X/n についての平均と分散も、すでに定まっている.
平均については、確率変数 X がいっせいに 1/n 倍されるので
$$
\mbox{(X/n の平均)} = \frac{1}{n} × np = p
$$
分散については、
$$
\mbox{(確率変数の分散の定義)}=\sum_{i=1}^n (\mbox{}X_i\mbox{のとりうる値} - \mbox{平均})^2 \times \mbox{(その値をとる確率)}
$$
の定義を眺めると、Xのとりうる値すべて と 平均(期待値) が 1/n 倍され、その差を2乗したものなので
$$
\mbox{(X/n の分散)}=\frac{1}{n^2} × np(1-p) = \frac{p(1-p)}{n}
$$
である.
( 余談だが、別の表現では「すべての世帯(実際は不明)」を n 世帯 ごとに小分けして調査していくと、 確率変数としての p^ は二項分布に従う。ともいえる )
分散から標準偏差を求めることができるので
$$
(\hat{p}\mbox{の標準偏差})=\sqrt{\frac{p(1-p)}{n}}
$$
このとき、標準偏差を1%以下にするには
$$
\sqrt{\frac{p(1-p)}{n}}\leqq0.01 \\
\mbox{すなわち} \\
n \geqq 10000p(1-p)
$$
となる n を探す。
p(1-p)の最大値は 1/4 (p=1/2のとき)※なので
※p(1-p) は (0, 0)と(1, 0)を通る上に凸な2次曲線. かつpは0から1の範囲をとりうる.→ p(1-p)の最大値は1/4
$$
\begin{align}
n & \geqq 10000 \times \frac{1}{4} \\
n & \geqq 2500 \cdots \mbox{(答え)}
\end{align}
$$
問い②
100 世帯を無作為に抽出して調査すると、ある番組を見ていたのは 20 世帯だった.
「全世帯のうち、その番組を見ていた世帯」の割合を p とするとき、
p の95%信頼区間の視聴率は 何%~何% か?
また、1000 世帯を調査して、その番組を見ていた世帯が 200 世帯だった場合はどうか?
解答
「抽出された n 世帯のうち、その番組を見ている世帯の数」を X とすると
X は確率変数で二項分布B(n, p)に従う.
(中心極限定理により平均値の周辺に質量が多く分布する)
また、 n が十分に大きいとき、X の確率密度は正規分布に近似する(ド・モアブル=ラプラスの定理)
(正規分布へ近似はn>30が目安。 n のサイズが小さいときは t分布として解く)
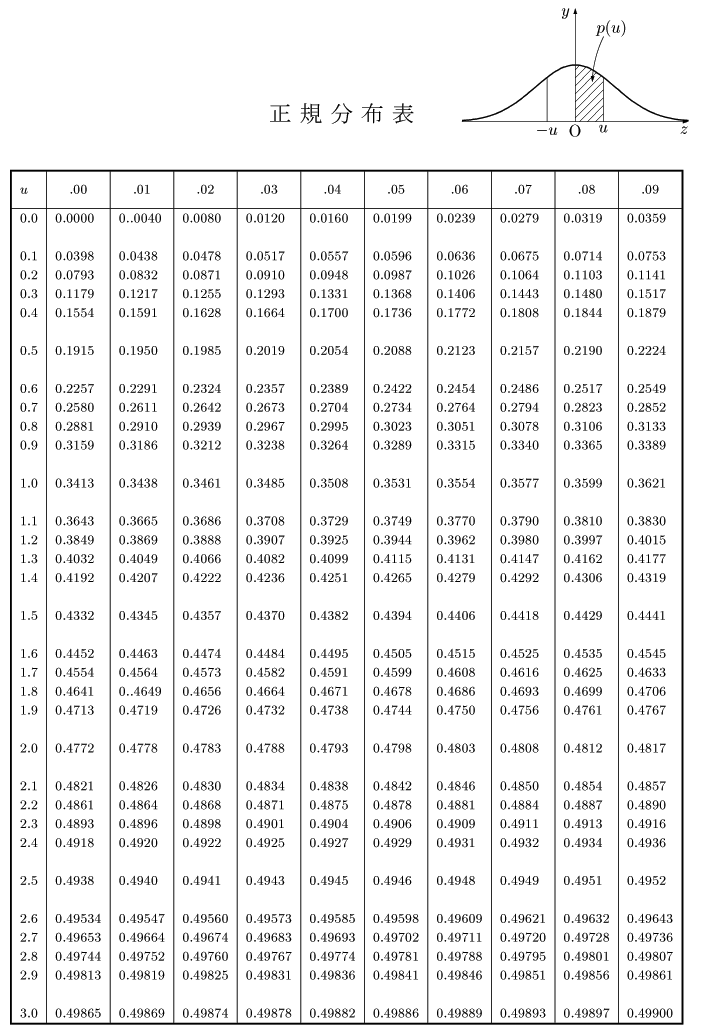
X の確率密度の標準偏差を σ とすると、正規分布表より |z|=1.96 のとき確率分布の95%を占めるので
$$
\hat{p}-1.96×\sigma \leqq p \leqq \hat{p}+1.96×\sigma \\
\mbox{すなわち} \\
\hat{p}-1.96×\sqrt{\frac{p(1-p)}{n}} \leqq p \leqq \hat{p}+1.96×\sqrt{\frac{p(1-p)}{n}} \\
p\mbox{と}\hat{p}\mbox{は近いはずなので}p\mbox{を}\hat{p}\mbox{で置き換えると} \\
\hat{p}-1.96×\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \leqq p \leqq \hat{p}+1.96×\sqrt{\frac{\hat{p}(1-\hat{p}}{n}} \\
$$
n = 100, p^=0.2 なので
$$
0.2-1.96×\sqrt{\frac{0.2(1-0.2))}{100}} \leqq p \leqq 0.2+1.96×\sqrt{\frac{0.2(1-0.2)}{100}} \\
0.1216 \leqq p \leqq 0.2784 \\
\cdots \mbox{(答え)}
$$
1000 世帯を調査して、その番組を見ていた世帯が 200 世帯だった場合、
n = 1000, p^=0.2 なので
$$
0.1752 \leqq p \leqq 0.2247
$$
『精度が高まり、誤差の範囲が縮まった』……(答え)
(一般にn を大きくすると精度が高まり誤差の範囲が縮まる)
なお、答えの計算にはpythonを使用
# 確率分布の下限と上限を返す関数
import math
def get_error_min_max(n, p_, z=1.96):
sigma = math.sqrt(p_*(1-p_)/n)
min_ = p_-z*sigma
max_ = p_+z*sigma
return 'min: {}, max: {}'.format(min_, max_)
# 100 世帯を調査して 20 世帯が番組を見ていたとき、 95% 信頼区間の下限と上限
# ⇛ n=1000, p^=0.2, z=1.96のとき
print(get_error_min_max(n=100, p_=0.2, z=1.96))
# 1000 世帯を調査して 20 世帯が番組を見ていたとき、 95% 信頼区間の下限と上限
# n = 1000 p^=0.2 z=1.96のとき
print(get_error_min_max(n=1000, p_=0.2, z=1.96))
選挙の開票途中で「当確」
投票者数10万人の選挙で候補者A, Bが争う.
開票数が 10000 のとき A は5050票 B は4950票であった。
問い①
候補者A, Bの最終得票率 p_a, p_b を信頼区間 95%で表わせ。
解答
現在の得票率をそれぞれ p_a^, p_b^ とすると
p_a^ = 5050 / 10000 = 0.505
p_b^ = 4950 / 10000 = 0.495
となり最終得票率もこれに近いと推定する。
最終得票率 p は95%の確からしさで
$$
\hat{p} \pm 1.96×\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}
$$
の範囲に入ると推定できるため
print(get_error_min_max(n=10000, p_=0.505, z=1.96))
print(get_error_min_max(n=10000, p_=0.495, z=1.96))
# min: 0.49520049001225064, max: 0.5147995099877494
# min: 0.48520049001225063, max: 0.5047995099877494
問い②
候補者A に当選確実を出すには、開票数がいくつを超えたときか?
(※95%以上の確からしさをもつ予測を以て当選確実とする)
解答
P_a^ の下限が 50%を超えたとき、
95%の確からしさで候補者 A が当選確実といえるので、
(候補者が3人なら (P_a^ の下限) > (P_b^ の上限) かつ (P_a^ の下限) < (P_c^ の上限)かな?)
$$
\hat{p_a} - 1.96×\sqrt{\frac{\hat{p_a}(1-\hat{p_a})}{n}} \geqq 0.5
$$
となる n を探す。p_a^ = 0.505 なので、
$$
\begin{align}
0.505 - 1.96×\sqrt{\frac{0.505(1-0.505)}{n}} &\geqq 0.5 \\
-0.9799×\sqrt{\frac{1}{n}} &\geqq -0.005 \\
\sqrt{\frac{1}{n}} &\geqq 0.00510256 \\
\frac{1}{n} &\geqq 0.000025 \\
n &\geqq 40000 \cdots \mbox{(答え)} \\
\end{align}
$$
正確には
n = 38413 のとき0.50000005 < p_a^
print(get_error_min_max(40000, .505))
print(get_error_min_max(40000, .495))
# min: 0.5001002450061253, max: 0.5098997549938747
# min: 0.4901002450061253, max: 0.4998997549938747
print(get_error_min_max(38413, .505))
# min: 0.5000000547734237, max: 0.5099999452265763