6-4b 精度分析ノード:回帰[出力タブ]
1.ノードの目的
予測精度を出力します。名義型やフラグ型予測モデルの場合には、以下の記事のように一致行列やAUC、精度を出力します。
SPSS Modeler ノードリファレンス 6-4a 精度分析 - Qiita
数値型の予測モデル（回帰）の場合には二乗平均平方根誤差 (RMSE)や絶対平均誤差(MAE)のモデルの精度指標を出力します。この記事では数値型の予測モデルの場合の使い方を説明します。
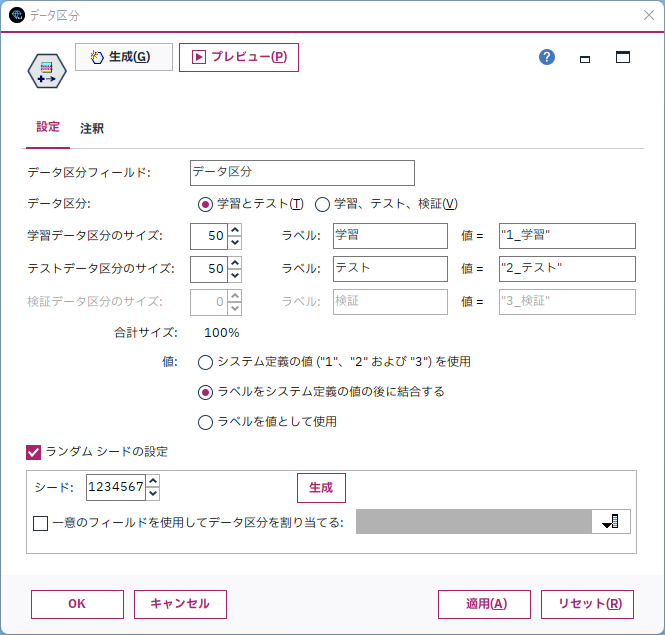
精度確認する際に、[データ分割]ノードと共に利用します。
2.解説動画（60秒）
TBD
3.クイックスタート
サンプルストリーム
- テスト環境
- Modeler 18.4
- Windows 11 64bit
以下の線形回帰の記事で作ったデータを使います。
利用データ
右クリックでリンク先を保存してください。
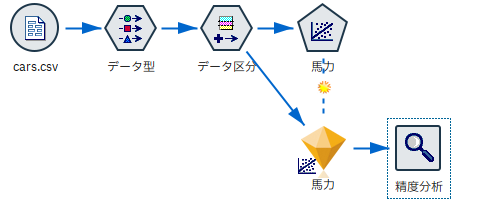
[可変長ファイル]に[データ型]、[データ区分]、[線形回帰]を接続します。
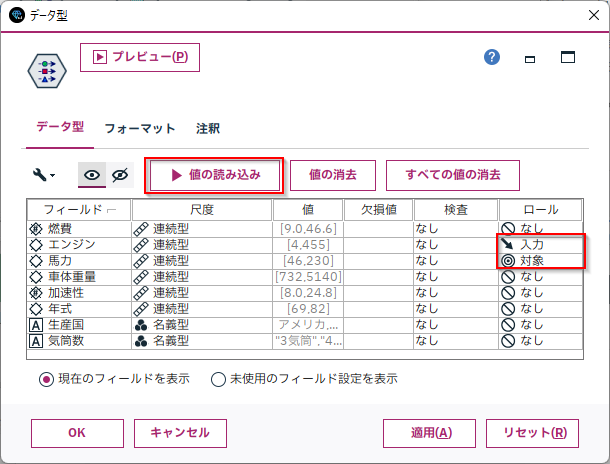
[データ型]で[値の読み込み]ボタンを押した後に、予測の[ロール]を設定します。今回はエンジンから馬力を予測する単回帰モデルを作ります。
[データ区分]には何も設定をしません。
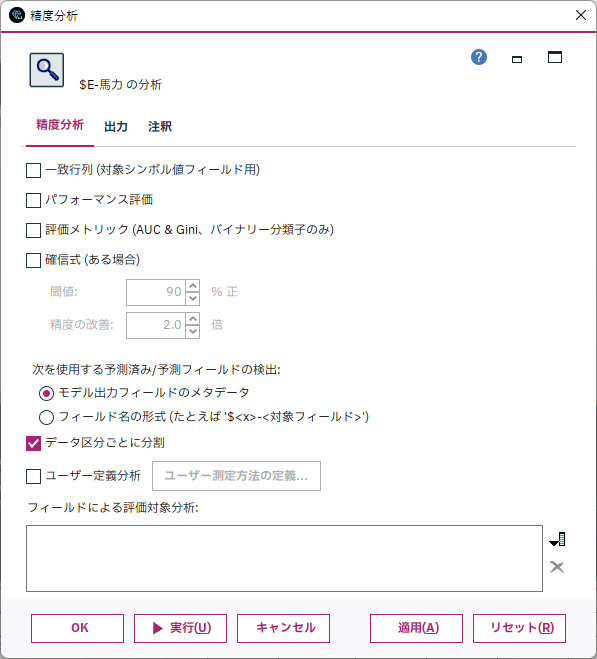
[線形回帰]を実行します。出来上がったモデルナゲットに[精度分析]を接続します。
[精度分析]には何も設定をしません。
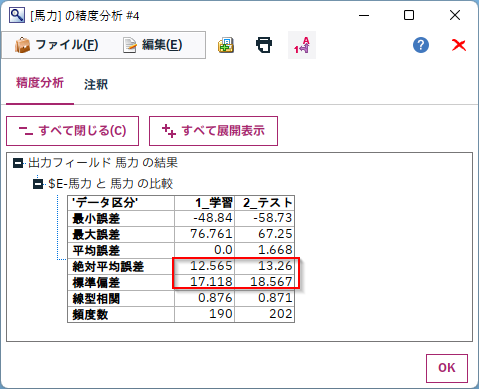
以下の精度指標が学習とテストに分けて表示されます。
精度分析:回帰の指標
| 指標 | 指標の意味 | 読み方 |
|---|---|---|
| 最小誤差 | 実測値と予測値の差の最小値 | 大きな外れ値がないか。 過小評価されている傾向がないか |
| 最大誤差 | 実測値と予測値の差の最大値 | 大きな外れ値がないか。 過大評価されている傾向がないか |
| 平均誤差 | 実測値と予測値の差の平均 | 小さいほど実測値と予測値は一致。 ただし、＋、－が相殺されるため、ゼロでも実測値と予測値が一致しているとは判断できない。 線形回帰モデルで学習データの場合はゼロになる。 |
| 絶対平均誤差(Mean Absolute Error) | 実測値と予測値の差の絶対値の平均 | 小さいほど実測値と予測値は一致。 ＋、－の相殺を防ぐため実測値と予測値の差の絶対値の平均をとっている ゼロは実測値と予測値の一致を意味 |
| 二乗平均平方根誤差(標準偏差)(Root Mean Squared Error) | 実測値と予測値の差の平均からのばらつき | 小さいほど実測値と予測値は一致。 ＋、－の相殺を防ぐため実測値と予測値の差を2乗を平均して平方根をとっている ゼロは実測値と予測値の一致を意味 注)外れ値の影響を受けやすい |
| 線型相関 | 実測値と予測値の相関(線型の関係性 | 予測値が実測値をどれだけ説明できているか) -1から+1の範囲 +1に近い値は強い正の相関、-1に近い値は強い負の相関 絶対値が1に近いほど強い相関を表し、0に近いほど弱い相関を表す 1は実測値と予測値の一致を意味 |
これらの中で、よく参照するのは標準偏差、絶対平均誤差です。
どちらも平均でどのくらいの誤差があるかという指標になります。予測値と同じスケールで誤差の大きさを検討することが可能です。
標準偏差というのは、わかりにくいのですが、二乗平均平方根誤差 (RMSE)のことです。
線形回帰については以下の記事で解説されています。
SPSS Modeler ノードリファレンス 5-1 線型回帰
4.TIPS:平均絶対パーセント誤差MAPE
回帰の指標には上であげたもの以外にもあり、値の範囲が大きい回帰であれば、平均絶対パーセント誤差（MAPE）を使うことがあります。
例えば、お店の売上を予測した場合に平均100万円という誤差があったとして、売上300万円の店Aと売上3000万の店Bではそもそもの売上規模に違いがあるため、その誤差が許容できるのかどうか判断は困難です。
その場合、誤差を目的変数のパーセントで割った数値の方が誤差の判断には適切かもしれません。上の例なら、店Aで30％、店Bで3％の誤差となります。
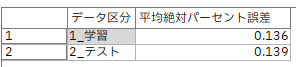
これらを平均した平均絶対パーセント誤差（MAPE）という指標があります。
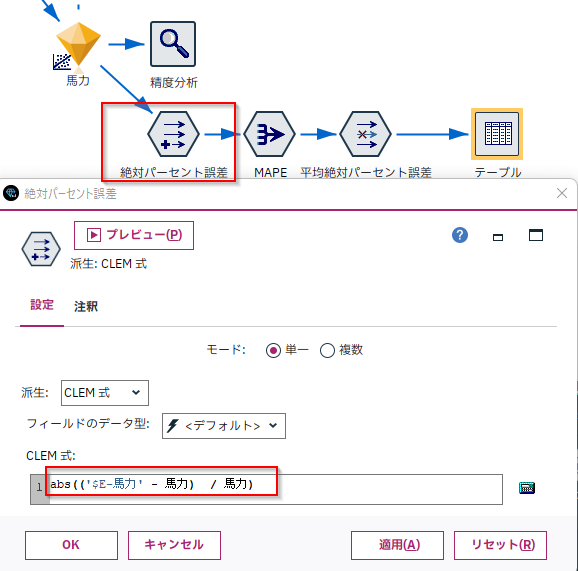
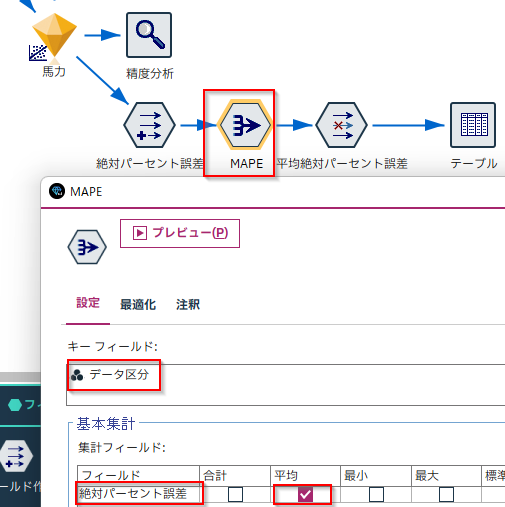
精度分析ノードでは自動計算されませんので、計算する必要があります。
フィールド作成ノードで絶対パーセント誤差を算出し、
集計ノードでその平均をとりMAPEを計算します。
以下のような結果が得られます。
5.参考情報
ノードのヘルプ
SPSS Modeler ノードリファレンス目次
SPSS Modelerの回帰モデル評価のための精度分析ノードを、pythonに書き換える - Qiita
MAPE(平均絶対パーセント誤差、平均絶対誤差率)とは ~Wikipedia翻訳~ - Qiita