SPSS Modelerの線形回帰ノードをPythonのscikit-learnとstatsmodelsで書き換えてみます。
以下の@416nishimaki さんの記事でModelerでの使い方は解説されていますので、この内容をscikitlearnとstatsmodelsで行ってみます。
SPSS Modeler ノードリファレンス 5-1 線型回帰 - Qiita
pythonで線形回帰のモデルをつくるにはscikit-learnとstatsmodelsの二つのパッケージがありました。
それぞれで作ってみたいと思います。
1m.単回帰分析Modeler
Modelerでは以下のようにロールで説明変数(入力)と目的変数(対象)を定義します。
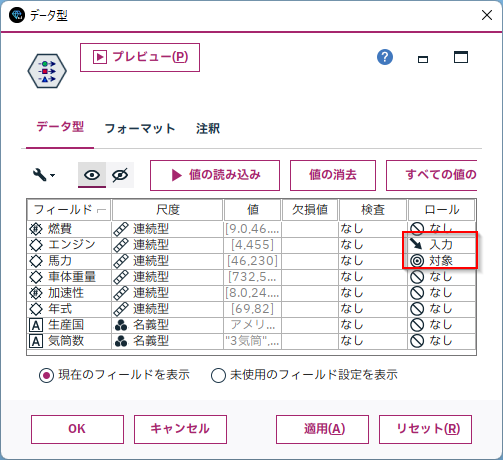
そして、モデル作成は「線形回帰ノード」を接続して実行します。なお、「エキスパート」タブの「出力」設定で各「詳細出力のオプション」にチェックを付けておくとモデルに様々な指標を出力してくれます。
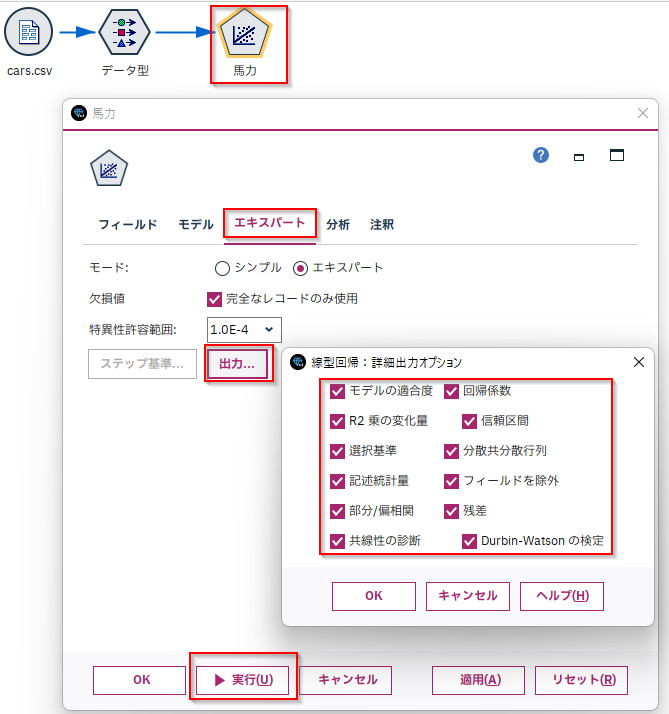
できたモデルの要約タブの「精度分析」をみると係数と切片が書かれています。
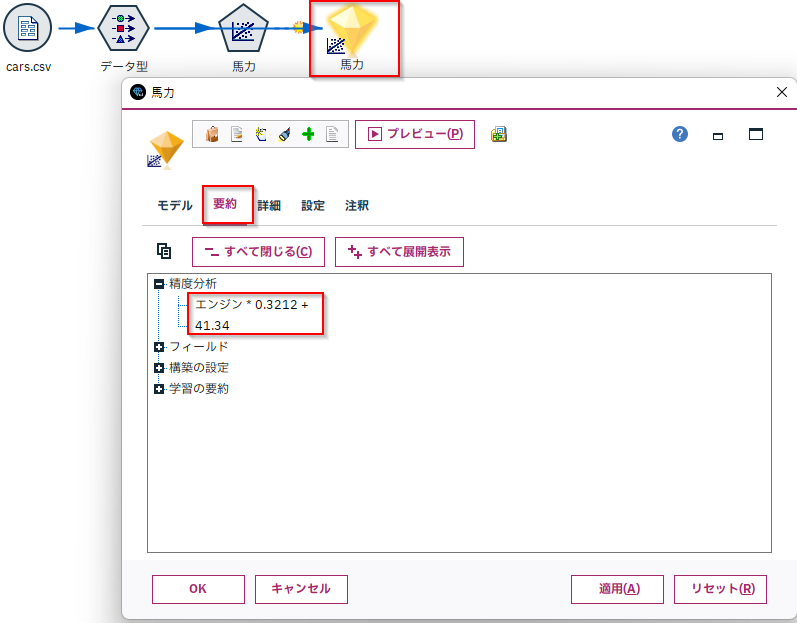
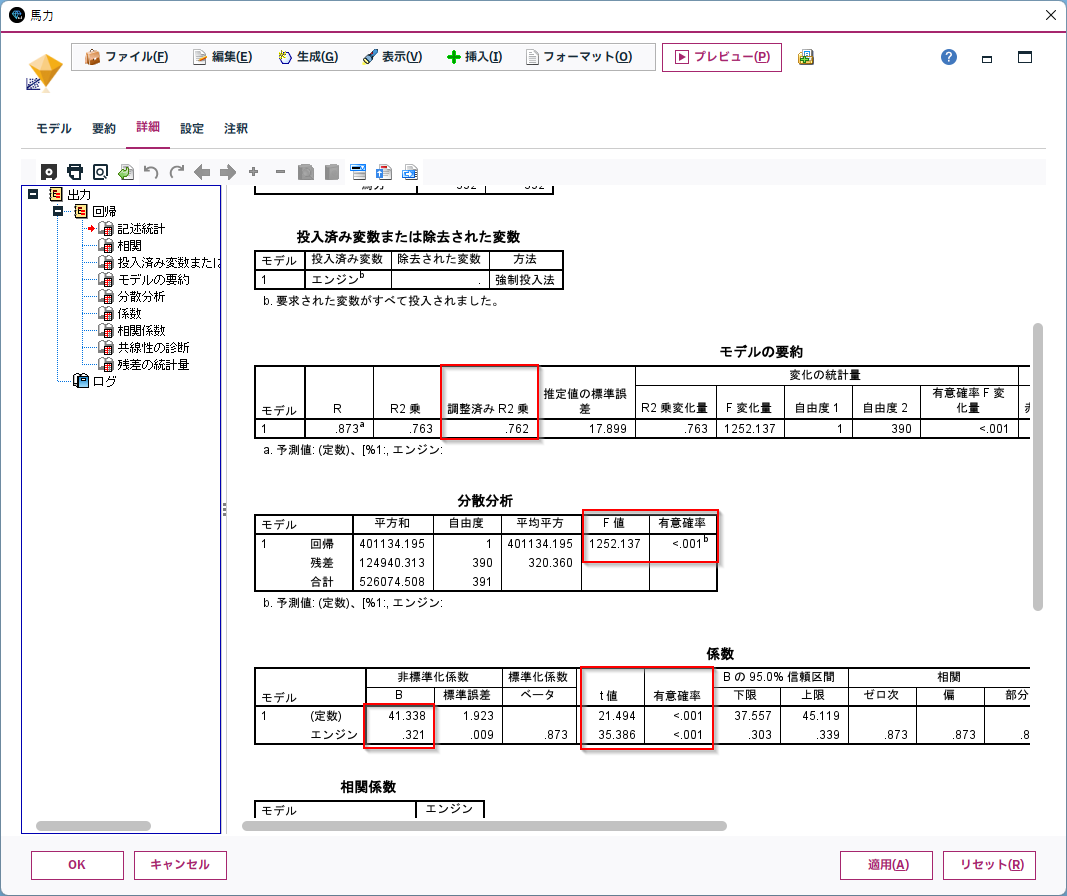
「詳細」タブをみると、さまざまなモデルの様々な指標がまとめられています。
係数(coef)切片(constのcoef)はもちろん、調整済みR2乗(Adj. R-squared)、F値の検定(Prob (F-statistic))、説明変数のt値の検定(P>|t|)などの詳細な情報が取れます。
1sk.単回帰分析scikit-learn
scikit-learnでは、まず、元のDataFrameから説明変数と目的変数に絞り込んだDataFrameや配列を準備します。
# 説明変数
X = df[['エンジン']]
# 目的変数
Y = df['馬力']
モデルは以下のように作ります。fitで計算が走ります。
# 線形回帰のモデルを作成
lr = LinearRegression()
lr.fit(X, Y)
回帰式の係数と切片はcoef_とinterept_に入ります。
#回帰式の係数と切片を出力
print('coefficient = ', lr.coef_[0])
print('intercept = ', lr.intercept_)
coefficient = 0.32119242933373704
intercept = 41.33771174883606
指標としては、R2乗値を得ることができます。scoreに、説明変数と目的変数を改めて与えます。
# R2乗値を出力
print('r^2 = ', lr.score(X,Y))
r^2 = 0.7625045295579075
その他の指標はsklearn.metricsにある以下の指標を得ることができます。R2乗はこちらでも計算できます。
調整済みR2乗値、p値、F値、VIFなどの統計的な指標がないのが特徴といえると思います。発想が機械学習なために、当たりの良さの指標がメインなのだと思います。
R² score, the coefficient of determination
Mean absolute error
Mean squared error
Mean squared logarithmic error
Mean absolute percentage error
Median absolute error
Max error
Explained variance score
Mean Poisson, Gamma, and Tweedie deviances
Pinball loss
D² score
D² Tweedie score
D² pinball score
D² absolute error score
- 参照:3.3. Metrics and scoring: quantifying the quality of predictions — scikit-learn 1.1.1 documentation
ここではR2乗値と平均二乗誤差(MSE)を計算してみます。
predictでスコアリング結果Y_predを得て、学習データの目的変数Yと比較して計算します。
#モデルの評価
Y_pred = lr.predict(X) # 学習データに対する目的変数を予測
# R2乗値を出力
from sklearn.metrics import r2_score
print('r^2 data: ', r2_score(Y, Y_pred))
# 平均二乗誤差を出力
from sklearn.metrics import mean_squared_error
print('MSE data: ', mean_squared_error(Y, Y_pred))
r^2 data: 0.7625045295579075
MSE data: 318.72528745575494
1st.単回帰分析statsmodels
statsmodelsでも、まず、元のDataFrameから説明変数と目的変数に絞り込んだDataFrameや配列を準備します。
# 説明変数
X = df[['エンジン']]
# 目的変数
Y = df['馬力']
X = sm.add_constant(X)
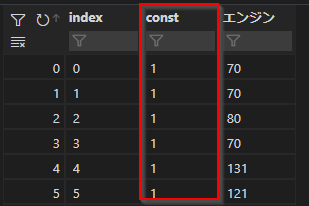
やや、特殊なのはadd_constantで定数列を追加するところです。以下のように「1」が入った「const」という列が追加されます。
モデルは以下のように作ります。fitで計算が走ります。
OLS(Ordinary Least Squares regression)は最小二乗回帰という意味です。
# 線形回帰のモデルを作成
model = sm.OLS(Y, X)
res = model.fit()
モデル内容の詳細はsummaryで得られます。
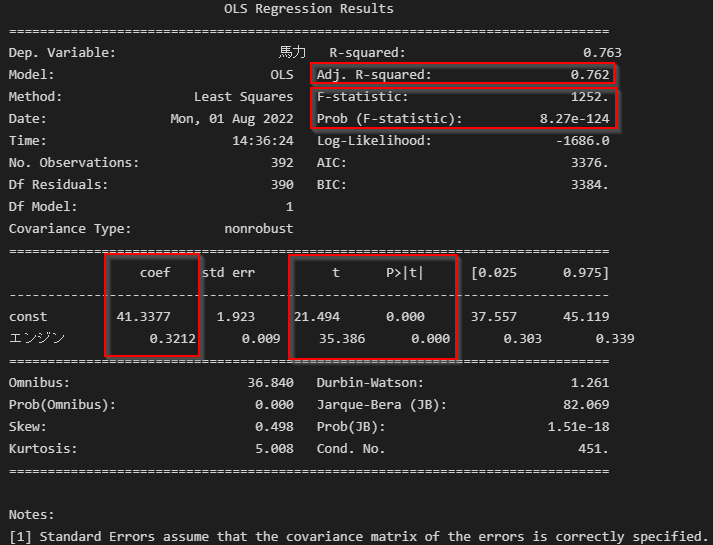
係数(coef)切片(constのcoef)はもちろん、Modelerと同様に、調整済みR2乗(Adj. R-squared)、F値の検定(Prob (F-statistic))、説明変数のt値の検定(P>|t|)などの詳細な情報が取れます。
#モデルの内容/評価の表示
print(res.summary())
- 参考
- 【簡単】Pythonのstatsmodelsで重回帰分析を行う方法 | ジコログ
- statsmodelsによる線形回帰 入門 - Qiita
1m.重回帰分析Modeler
Modelerでは以下のようにロールで説明変数(入力)と目的変数(対象)を定義します。
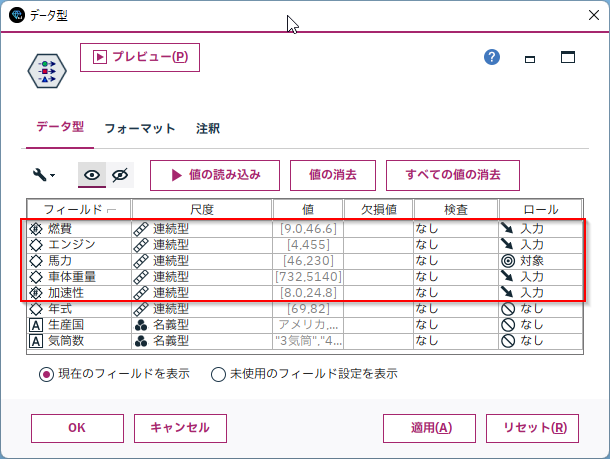
作成の仕方は単回帰と同じです。
できたモデルの要約タブの「精度分析」をみると係数と切片が書かれています。
「詳細」タブをみると、さまざまなモデルの様々な指標がまとめられています。
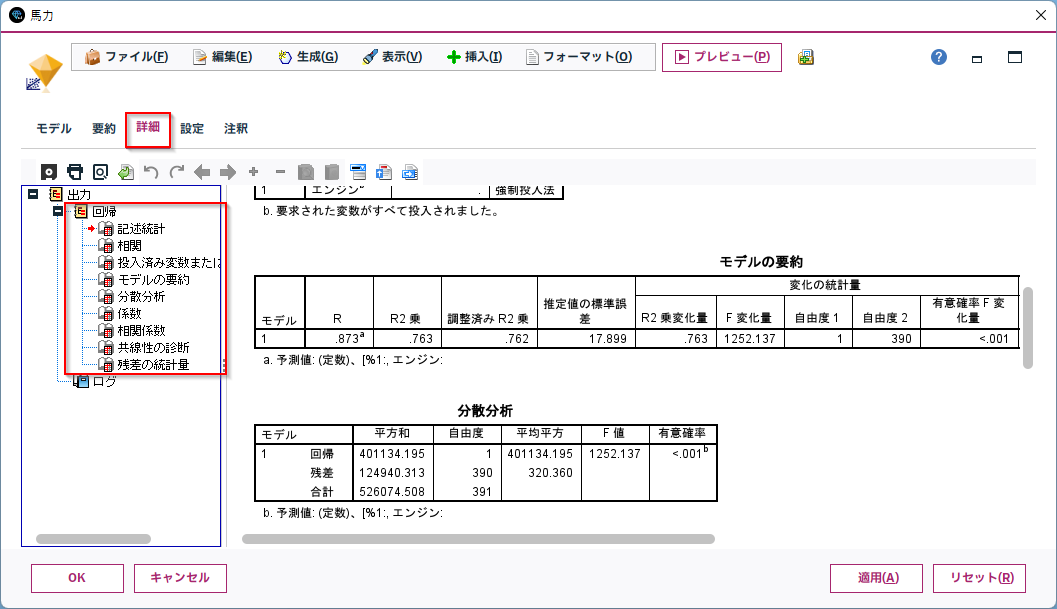
標準化係数で複数の説明変数の影響の大きさを比較したり、
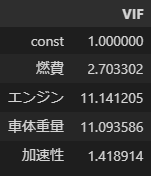
VIFで多重共線性を確認することもできます。

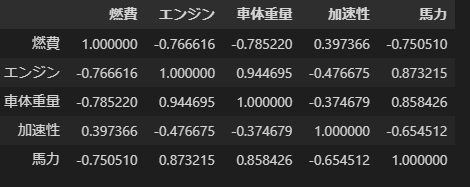
また、多重共線性のある変数の組み合わせを探すために、変数同士の相関係数行列もでています。
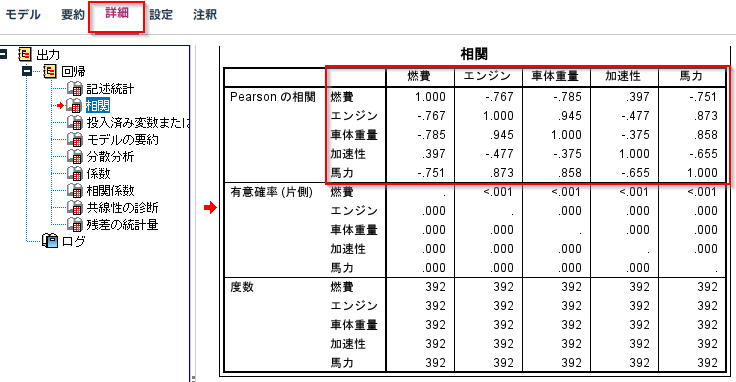
2sk.重回帰分析scikit-learn
scikit-learnでは、説明変数の指定が
X = df[['燃費', 'エンジン', '車体重量', '加速性']]
のように、ちがうだけであとは単回帰と同じです。
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 説明変数
X = df[['燃費', 'エンジン', '車体重量', '加速性']]
# 目的変数
Y = df['馬力']
# 線形回帰のモデルを作成
lr = LinearRegression()
lr.fit(X, Y)
#回帰式の係数と切片を出力
print('coefficient = ', lr.coef_)
print('intercept = ', lr.intercept_)
# R2乗値を出力
print('r^2 = ', lr.score(X,Y))
#モデルの評価
Y_pred = lr.predict(X) # 学習データに対する目的変数を予測
# R2乗値を出力
from sklearn.metrics import r2_score
print('r^2 data: ', r2_score(Y, Y_pred))
# 平均二乗誤差を出力
from sklearn.metrics import mean_squared_error
print('MSE data: ', mean_squared_error(Y, Y_pred))
coefficient = [-0.43655748 0.05634613 0.02204664 -4.86622564]
intercept = 112.74898151587317
r^2 = 0.8714973704899913
r^2 data: 0.8714973704899913
MSE data: 172.45397334592232
2st.重回帰分析statsmodels
statsmodelsでも、説明変数の指定が
X = df[['燃費', 'エンジン', '車体重量', '加速性']]
のように、ちがうだけであとは単回帰と同じです。
# 説明変数
X = df[['燃費', 'エンジン', '車体重量', '加速性']]
# 目的変数
Y = df['馬力']
X = sm.add_constant(X)
# 線形回帰のモデルを作成
model = sm.OLS(Y, X)
res = model.fit()
#モデルの内容/評価の表示
print(res.summary())
Output exceeds the size limit. Open the full output data in a text editor
OLS Regression Results
==============================================================================
Dep. Variable: 馬力 R-squared: 0.871
Model: OLS Adj. R-squared: 0.870
Method: Least Squares F-statistic: 656.2
Date: Tue, 26 Jul 2022 Prob (F-statistic): 6.37e-171
Time: 10:42:24 Log-Likelihood: -1565.6
No. Observations: 392 AIC: 3141.
Df Residuals: 387 BIC: 3161.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 112.7490 7.830 14.400 0.000 97.355 128.143
燃費 -0.4366 0.139 -3.145 0.002 -0.709 -0.164
エンジン 0.0563 0.022 2.519 0.012 0.012 0.100
車体重量 0.0220 0.003 8.355 0.000 0.017 0.027
加速性 -4.8662 0.298 -16.312 0.000 -5.453 -4.280
==============================================================================
Omnibus: 90.350 Durbin-Watson: 1.469
Prob(Omnibus): 0.000 Jarque-Bera (JB): 535.323
Skew: 0.821 Prob(JB): 5.70e-117
Kurtosis: 8.484 Cond. No. 3.59e+04
==============================================================================
...
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.59e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
2st-1.重回帰分析statsmodels 標準化係数
以下のModelerのように標準化係数を求める場合は、説明変数、目的変数を標準化してからモデルを作ります。
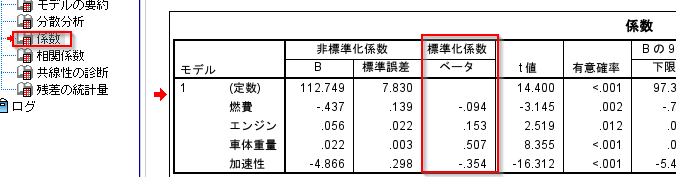
以下ではStandardScalerを使って各データを標準化してから線形回帰を行います。
import numpy as np
from sklearn.preprocessing import StandardScaler
# 標準化
scaler = StandardScaler()
df2 = df[['燃費', 'エンジン', '車体重量', '加速性','馬力']]
scaler.fit(np.array(df2))
df_std = scaler.transform(np.array(df2))
df_std = pd.DataFrame(df_std, columns=df2.columns)
# 説明変数
X = df_std[['燃費', 'エンジン', '車体重量', '加速性']]
# 目的変数
Y = df_std['馬力']
X = sm.add_constant(X)
# 線形回帰のモデルを作成
model = sm.OLS(Y, X)
res = model.fit()
#モデルの内容/評価の表示
print(res.summary())
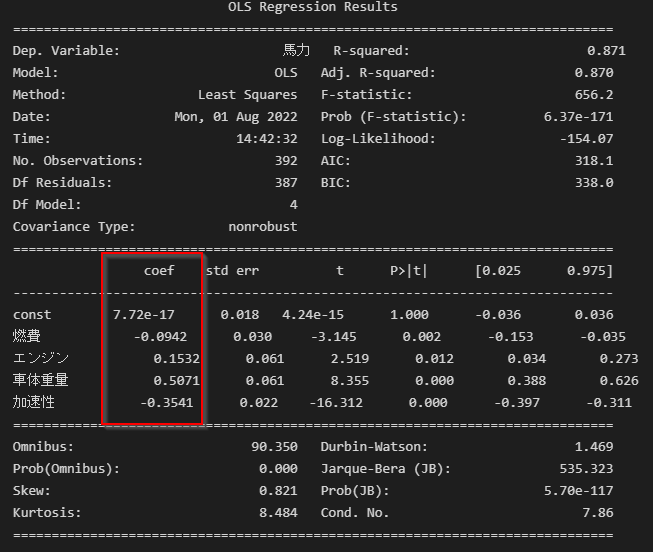
coefが標準化された係数になっています。
2st-2.重回帰分析statsmodels VIF
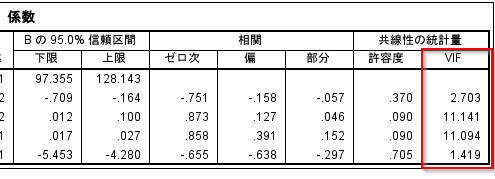
Modelerでは、多重共線性の発生指標のVIFもよく確認すると思います。
Pythonではstatsmodels.stats.outliers_influence.variance_inflation_factorで同じものが作れます。
#VIFの算出
from statsmodels.stats.outliers_influence import variance_inflation_factor as vif
num_cols = model.exog.shape[1] # 説明変数の列数
vifs = [vif(model.exog, i) for i in range(0, num_cols)]
pd.DataFrame(vifs, index=model.exog_names, columns=['VIF'])
2st-3.重回帰分析statsmodels 相関係数行列
Modelerでは以下のように変数同士の相関係数行列も出力されていました。これは多重共線性のある説明変数の組み合わせを探すのに便利です。
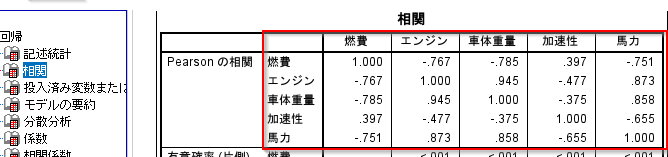
Pythonではcorrで同じものが作れます。
df[['燃費', 'エンジン', '車体重量', '加速性','馬力']].corr(method='pearson')
- 参考
- Python(StatsModels) で重回帰分析を理解し、分析の精度を上げる方法 | たぬハック
- statsmodels.stats.outliers_influence.variance_inflation_factor — statsmodels
3.主な指標
線形回帰でよくみる指標とそれがパッケージで算出できるかをまとめました。
| 指標 | Modeler線形回帰 | sklearn | statsmodels | |
|---|---|---|---|---|
| 性能 | 調整済みR2値 | 〇 | 〇 | 〇 |
| AIC | 〇 | × | 〇 | |
| BIC | 〇 | × | 〇 | |
| MSE | 〇精度分析ノード | 〇 | 〇 | |
| 検定 | F値 | 〇 | × | 〇 |
| t値 | 〇 | × | 〇 | |
| その他 | VIF(多重共線性) | 〇 | × | 〇 |
| Durbin-Watson(自己回帰) | 〇 | × | 〇 |
4. おまけ:変数選択
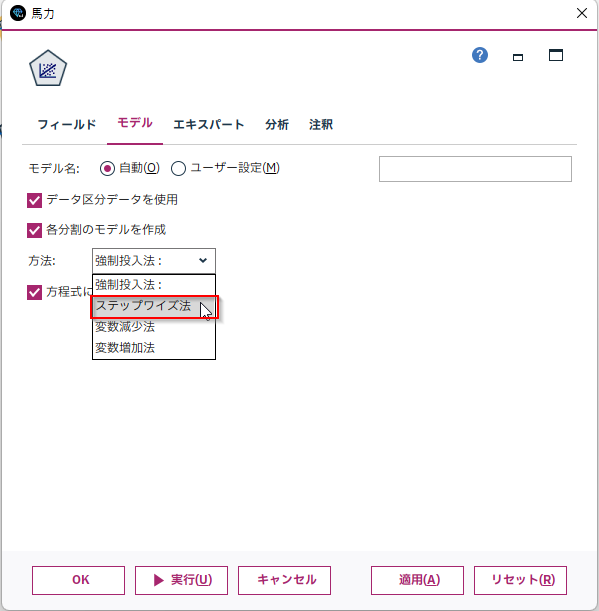
Modelerで変数選択をするときにはステップワイズで行うことがポピュラーですが、sklearnもstatsmodelsにも実装されていません。
以下のように、自分でステップワイズを実装する例があります。ちなみに以下はAICを基準にしていますが、Modelerの線形回帰ノードではF値が基準になっています。
pythonのstatsmodelsを使った重回帰分析で溶解度予測:AICによるモデル選択 | 化学の新しいカタチ
Pythonの世界だと、ラッソ回帰で変数選択をすることがポピュラーのようです。
AI Academy | ラッソ回帰とリッジ回帰
statsmodels.regression.linear_model.OLS.fit_regularized — statsmodels
Modelerでラッソ回帰をつくるにはGLEノードを使います。
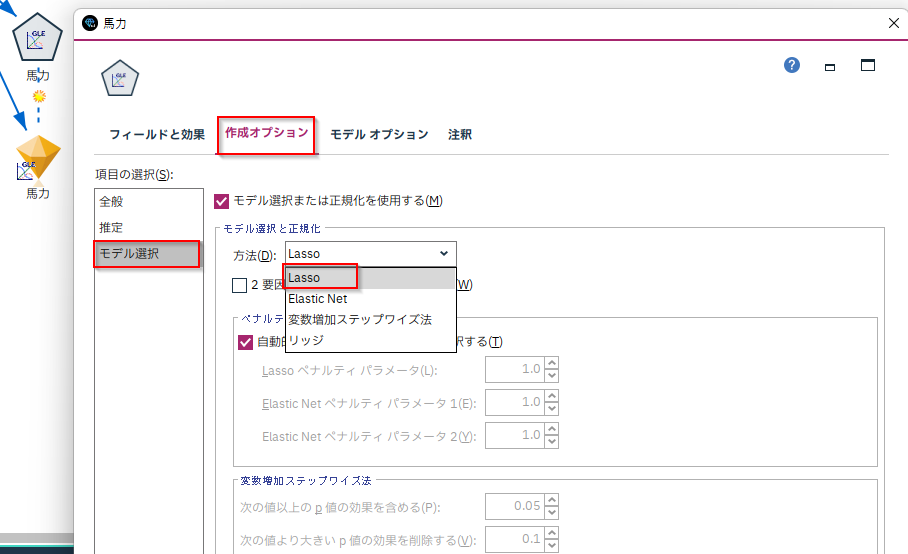
5. サンプル
サンプルは以下に置きました。
ストリーム
notebook
データ
■テスト環境
Modeler 18.4
Windows 10 64bit
Python 3.8.10
pandas 1.4.1
sklearn 1.1.1
statsmodels 0.13.2