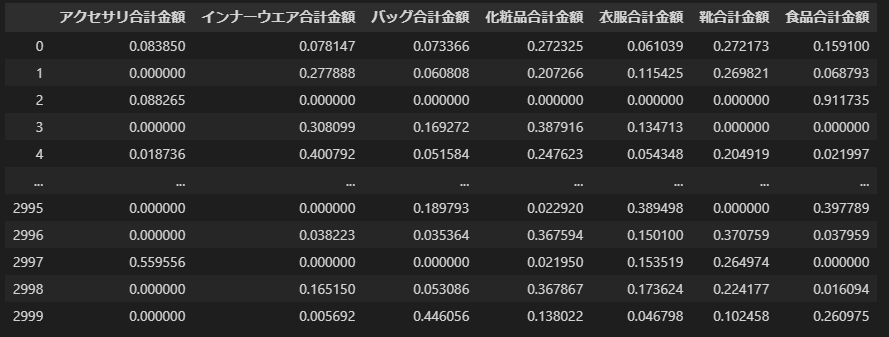
SPSS ModelerのK-MeansノードをPythonのscikit-learnで書き換えてみます。
以下の記事でModelerでの使い方は解説していますので、この内容をscikitlearnで行ってみます。
SPSS Modeler ノードリファレンス 5−18 K-Means(クラスター) - Qiita
1m.K-Meansの事前加工処理 Modeler
Modelerでは以下の事前処理を自動でやってくれます。
| 尺度 | スケーリング、ダミー変数化 | NULLの処理 |
|---|---|---|
| 連続型 | min-maxの0-1のスケーリング | 0.5で置換 |
| フラグ型 | 0,1へのダミー変数化 | 0.5で置換 |
| カテゴリ型 | one-hotで0,1へダミー変数化した上で重みをかける(デフォルトは√1/2) | 0.5で置換した上で重みをかける |
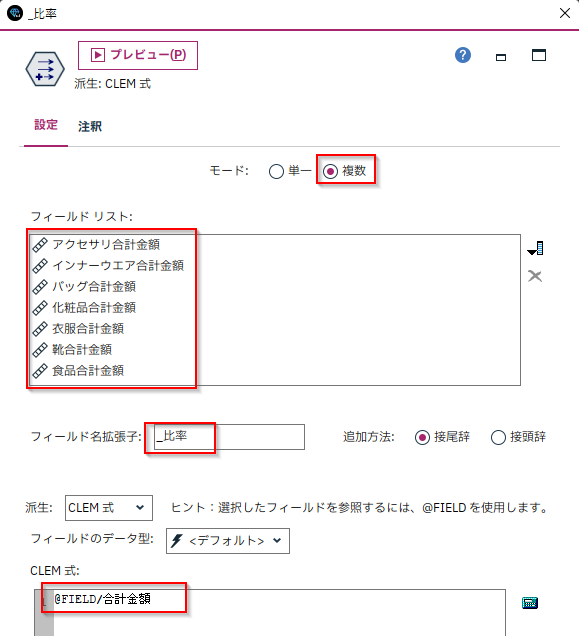
1p.K-Meansの事前加工処理 sklean
scikit-learnのK-Meansはフラグ型やカテゴリ型はダミー変数化が必要です。
欠損値は0.5への変換をします。
フラグ型
フラグ型はget_dummiesをつかってダミー変数化します。
drop_first=Trueをつけて1列にします。
dummy_na=TrueでNULLを識別できるようにします。
dtype=floatにしておきます。NULLを0.5に置き換えるためです。
df_km_gender = pd.get_dummies(df_km[['性別']], columns=[
'性別'], drop_first=True, dummy_na=True, dtype=float)
性別_nanにフラグが立っていれば0.5にします。
df_km_gender[df_km_gender['性別_nan'] != 0] = 0.5
df_km_gender = df_km_gender.drop(['性別_nan'], axis=1)
カテゴリ型
カテゴリ型はもうちょっと複雑になります。
まず、get_dummiesをつかってone-hotでダミー変数化します。
フラグ型と異なり、drop_first=Falseにします。これはフラグが立つカテゴリとフラグが立たないカテゴリで距離を変えないためです。例えば北区、東区、西区の3カテゴリがあったときに、西区のフラグはつくらないで北区=0,東区=0で表すと、北区と西区の距離は1になり、北区と東区の距離は√2になります。そのため西区のフラグもつくります。こうすると、北区と西区の距離も√2になり、すべてが等間隔になります。
しかしながら、例えば、「北区」=1、「西区」=1という2つのフラグとした場合、この2つのデータのユークリッド距離は√2になり1を超えてしまいます。
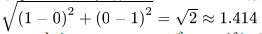
そのために、√1/2の重みをかけて以下のように2つのデータ間の距離を1にしています。
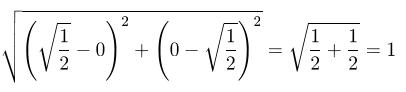
それがdummy_weight = np.sqrt(1/2)になります。
dummy_na=TrueでNULLを識別できるようにします。
dtype=floatにしておきます。NULLを0.5*dummy_weightに置き換えるためです。
dummy_weight = np.sqrt(1/2)
df_km_dist = pd.get_dummies(df_km[['地区']], columns=[
'地区'], dummy_na=True, dtype=float).mul(dummy_weight)
地区_nanにフラグが立っていれば0.5*dummy_weightにします。
df_km_dist[df_km_dist['地区_nan'] != 0] = 0.5*dummy_weight
df_km_dist = df_km_dist.drop(['地区_nan'], axis=1)
数値型
数値型のデータは各変数の尺度の影響をなくすために、MinMaxScalerで0-1の間の数値にスケーリングします。
mm = preprocessing.MinMaxScaler()
df_km_num = df_km[['アクセサリ合計金額', 'インナーウエア合計金額', 'バッグ合計金額', '化粧品合計金額',
'衣服合計金額', '靴合計金額', '食品合計金額']]
df_km_std = pd.DataFrame(mm.fit_transform(
df_km_num), columns=df_km_num.columns)
そしてnullは0.5に変換します
df_km_std = df_km_std.fillna(0.5)
最終的に、これらを結合します。
X = pd.concat([df_km_std,
df_km_gender,
df_km_dist], axis=1)
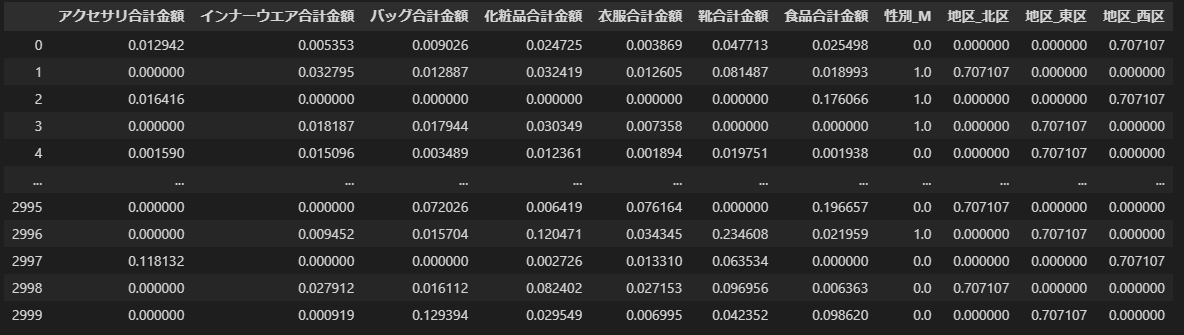
そして以下のようなデータに加工されました。フラグ型と数値型は0-1にスケーリングされ、カテゴリ型は0-0.707107にスケーリングされています。
- 参考
- 【Python】scikit-learnによる正規化/標準化/スケーリングの実装方法 |
- 【機械学習】クラスタリングをPythonで実装する|k-means | Smart-Hint
2m.K-Meansモデルの作成 Modeler
以下のようにロールで[データ型]タブでクラスタモデルに投入するフィールドを確定し、
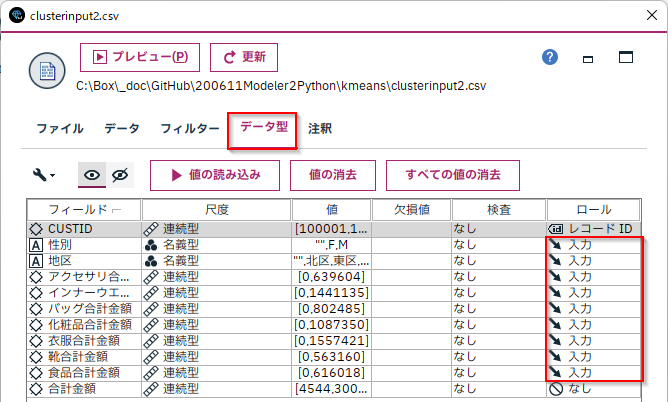
[K-Means]を接続して、実行するだけで「クラスター数」で指定した数にデータをクラスタリングします。
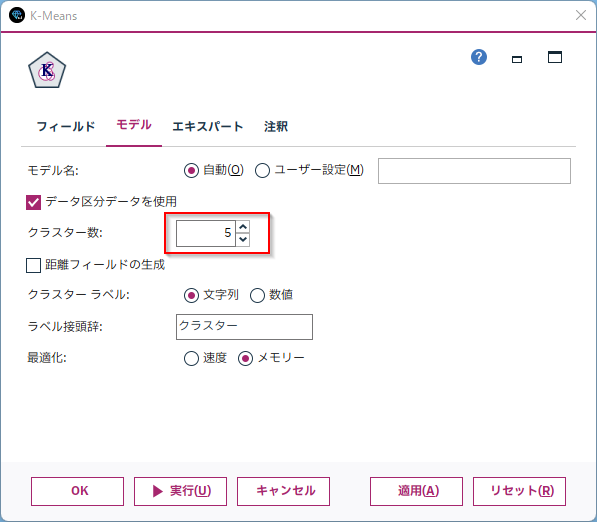
ちなみにエキスパートタブでは「最大反復数」、「収束基準」、「ダミー変数の調整値」を変更可能です。
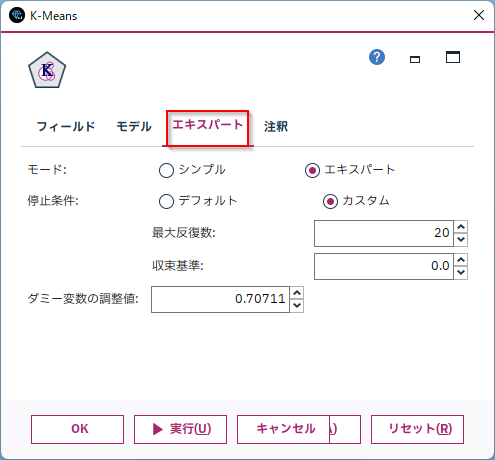
なお、Modelerでは初期のクラスタ中心を入力データ順に決めています。そのため、入力データの順序が変わると、結果が変わる可能性があります。
最初のレコードを使っていると書いてしまいましたが、以下の記事によるともっと賢い方法をつかって初期のクラスタ中心が離れるようにしているということでした。ただ、入力の順序には影響をうけていて、入力の順序を変えなければクラスタは毎回同じように作成されます。
How does the K-mean cluster node select initial records for clustering?
質問
K 平均クラスター ノードはどのようにクラスター化の初期レコードを選択しますか?疑似乱数ジェネレーターが使用されていますか?また、k-means アルゴリズムの初期サンプルを作成するためのシード値はどのように設定されていますか?ドキュメント (IBM Modeler Algorithms' Guide for Version 18.1.1) では、最初のレコードは最初のクラスターを作成するために使用されますが、その後のクラスターはどのように作成されるかがわかります。たとえば、5 の k-means が指定されている場合、最初の 5 つのレコードを使用して初期クラスターの重心を作成しますか?答え
K-Means では、最初の重心がデータ ポイントからランダムに選択されます。最初の重心が選択されると、アルゴリズムはデータセット全体で (ユークリッド距離に関して) 最も遠いレコードを探します。この点が第 2 重心になります。次に、レコードごとに、アルゴリズムはレコードと 2 つの重心の間の距離を計算し、2 つの最短距離を維持します。この値を d としましょう。 d 値が最も高いレコードが 3 番目の重心になります。すべてのセントロイドが初期化されるまで、以下同様です。
2p.K-Meansモデルの作成 sklearn
KMeansをつかってモデルを作成します。
| KMeansのパラメター | 内容 |
|---|---|
| n_clusters | 作成するクラスタ数を指定します。ここではModelerのデフォルト同様に5を設定しています。 |
| init=X[:5] |
|
| max_iter=20 | 最大反復数 |
| tol=0 | 収束基準 |
# モデルの作成
from sklearn.cluster import KMeans
# kmeansのモデルを作成
k=5
km = KMeans(n_clusters=k, max_iter=20 ,tol=0,n_init=1, init=X[:5])
km.fit(X)
# データが属するクラスターのラベルを取得
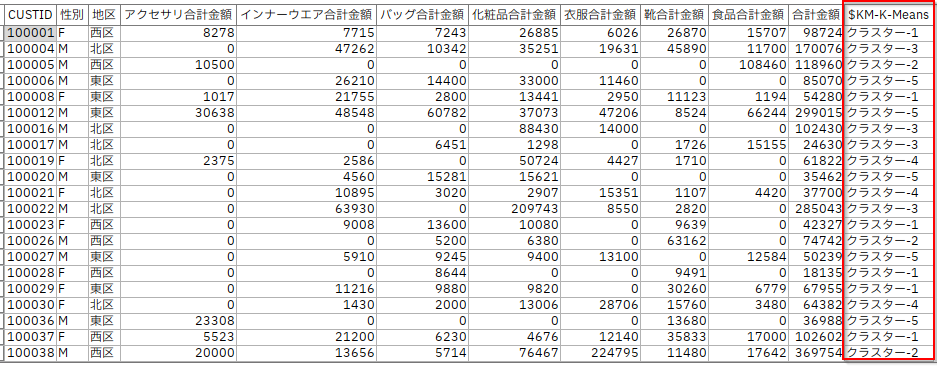
df_km['$KM-K-Kmeans']=km.predict(X)
df_km
結果は以下のように得られました。~~Modelerと同じ設定をしたつもりでしたが、~~Modelerは初期クラスタ中心をインテリジェントに選んでいますので、似たような傾向はみられるものの、結果は一致しませんでした。
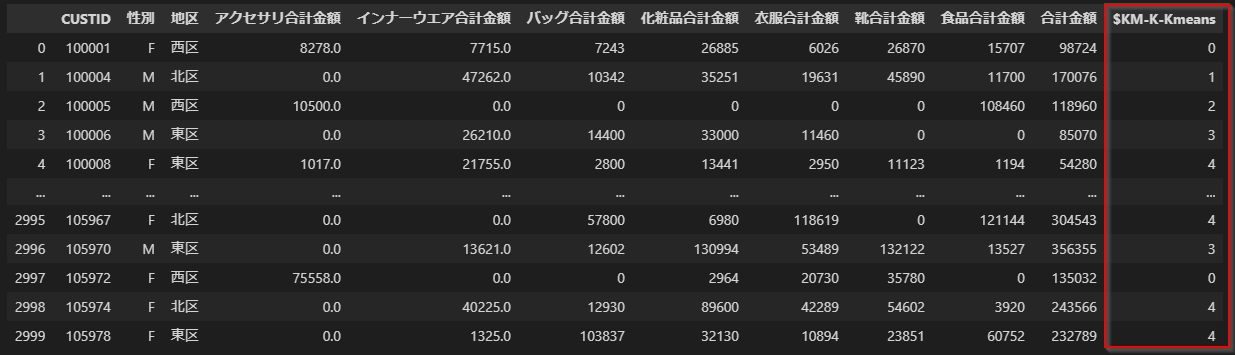
なお、sklearnのパラメーターには、Modelerにはない面白そうなものがありました。
| KMeansのパラメター | 内容 |
|---|---|
| init=‘k-means++’ | 初期クラスター中心を賢く選ぶサンプリング方法。k-meansは初期クラスター中心の影響を強く受けるので、賢く選んでくれるのは便利です。Modelerも賢く選んでいますが別の方法のようです |
| n_init | 初期クラスターを選ぶ回数。複数回トライして一番良いものを初期クラスターにします。 |
| algorithm | 一般的なlloydというアルゴリズムのほかにelkanというアルゴリズムも選ぶことができます |
ただ、今回のデータではこれらを使ってもあまり変わりませんでした。
- 参考
- sklearn.cluster.KMeans — scikit-learn 1.1.2 documentation
3m.クラスターの評価 Modeler
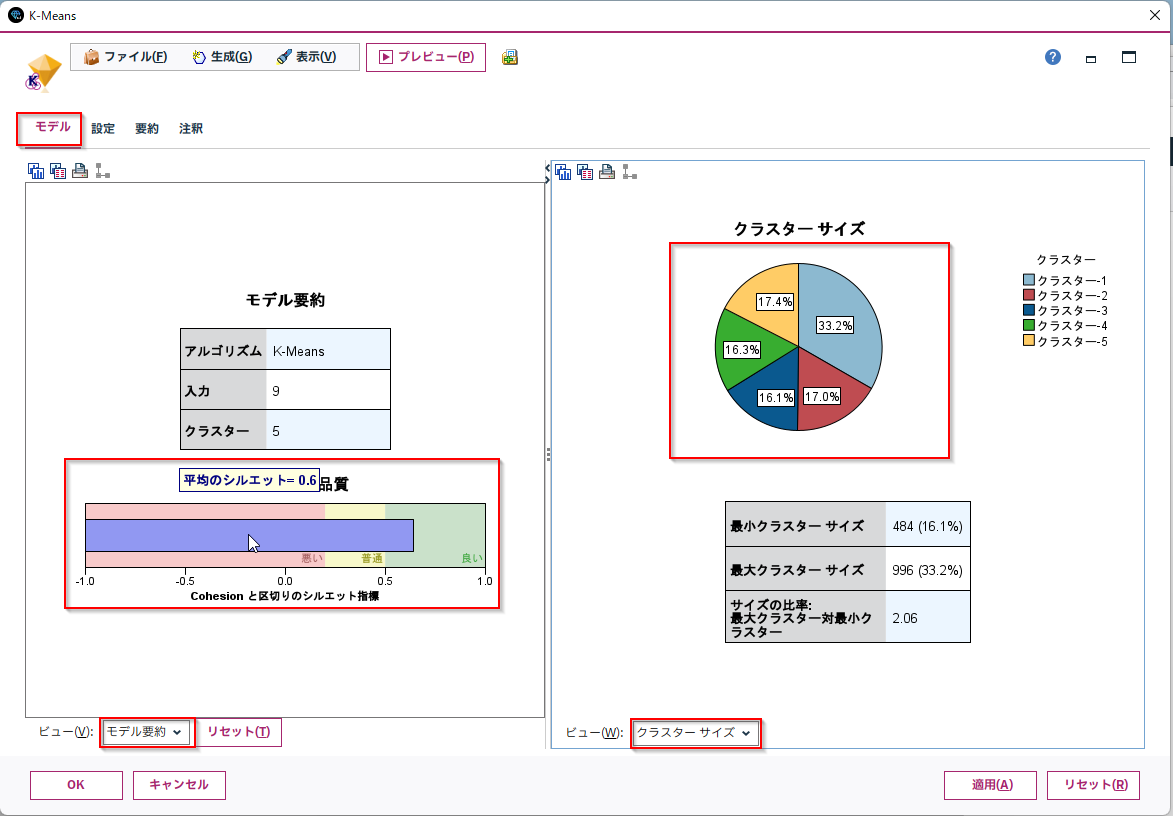
シルエット係数の平均値やクラスターサイズ
「モデル要約」のシルエット係数の平均値や「クラスターサイズ」などが確認できます。
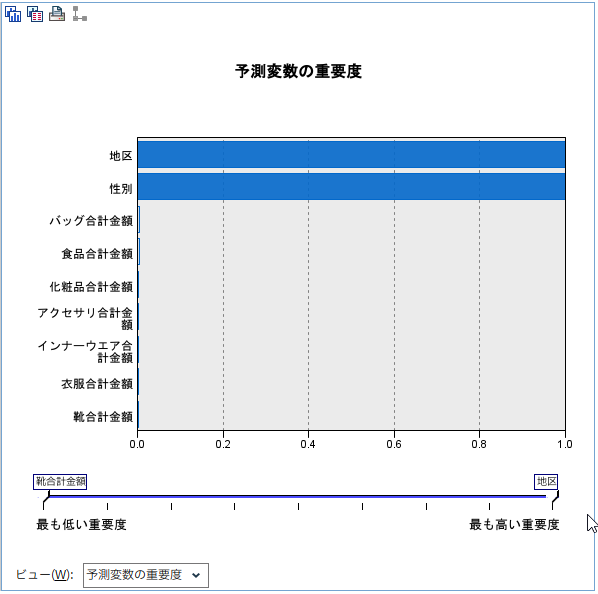
予測変数の重要度
「予測変数の重要度」説明変数の重要度が確認できます。
3p.クラスターの評価 sklean
シルエット係数の平均値
シルエット係数の平均値はfrom sklearn.metrics import silhouette_samplesで計算可能です。
from sklearn.metrics import silhouette_samples
silhouette_vals = silhouette_samples(X, df_km['$KM-K-Kmeans'])
print("シルエット係数平均: {:.2f}".format(silhouette_vals.mean()))
シルエット係数平均: 0.70
- 参考
- k-meansの最適なクラスター数を調べる方法 - Qiita
https://qiita.com/deaikei/items/11a10fde5bb47a2cf2c2#%E3%82%B7%E3%83%AB%E3%82%A8%E3%83%83%E3%83%88%E5%88%86%E6%9E%90%E3%81%A8%E3%81%AF
クラスターサイズ
クラスターサイズの確認はgroupbyなどで計算できます。
df_tmp=df_km[['$KM-K-Kmeans']].groupby('$KM-K-Kmeans').size()
df_size=pd.concat([df_tmp,df_tmp/df_tmp.sum()],axis=1)
df_size.columns=['度数','割合']
print(df_size)
print("最小のクラスターサイズ")
print(df_size.sort_values('度数').head(1))
print("最大のクラスターサイズ")
print(df_size.sort_values('度数',ascending=False).head(1))
print("サイズの比率:{:.2f}".format(df_size['度数'].min()/df_size['度数'].max()))
度数 割合
$KM-K-Kmeans
0 465 0.155000
1 482 0.160667
2 514 0.171333
3 524 0.174667
4 509 0.169667
5 470 0.156667
6 36 0.012000
最小のクラスターサイズ
度数 割合
$KM-K-Kmeans
6 36 0.012
最大のクラスターサイズ
度数 割合
$KM-K-Kmeans
3 524 0.174667
サイズの比率:0.07
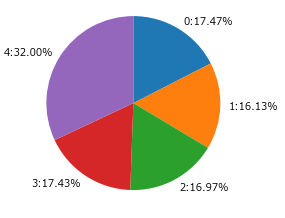
円グラフは以下で書けます。
ラベルにはクラスター番号と%を表示しています。
import matplotlib.pyplot as plt
%matplotlib inline
#文字化け対策
plt.rcParams['font.family'] = 'Meiryo'
fig = plt.figure()
fig.patch.set_facecolor('white')
#円グラフ作成
a=plt.pie(df_size['度数'], labels=["{:}:{:.2%}".format(i,df_size.loc[i]['割合']) for i in df_size.index], counterclock=False, startangle=90)
予測変数の重要度
Modelerで便利な説明変数の重要度についてはPythonではなさそうです。計算するライブラリーを発見できませんでした。
クラスタリングに効いた変数がわからないのは、変数選択をするにあたってかなり不便です。
4m.購入比率をもとにしたクラスターの作成 Modeler
金額ではなく、購入比率にすることで他者との比較をしやすくしてから、クラスタリングを作ることはよくあります。
顧客毎の合計金額から部門別に按分した7つの比率フィールドが作られました。

これを元にしてクラスターを作成します。クラスター作成手順は変わりません。
4p.購入比率をもとにしたクラスターの作成 sklearn
pandasの購入比率は.div(df_km1['合計金額'], axis=0)で計算できます。0-1.0の比率になったのでスケーリングは不要です。
#比率を計算
df_km_num1 = df_km1[['アクセサリ合計金額', 'インナーウエア合計金額', 'バッグ合計金額', '化粧品合計金額',
'衣服合計金額', '靴合計金額', '食品合計金額']].div(df_km1['合計金額'], axis=0).astype('float')
#数値列のnullは0.5に変換
df_km_std1 = df_km_std1.fillna(0.5)
これを元にしてクラスターを作成します。クラスター作成手順は変わりません。
5m.クラスターの解釈 Modeler
絶対分布グラフ
クラスタービューの「絶対分布」をみると各クラスターで商品購入比率の多い層の特徴を把握できます。
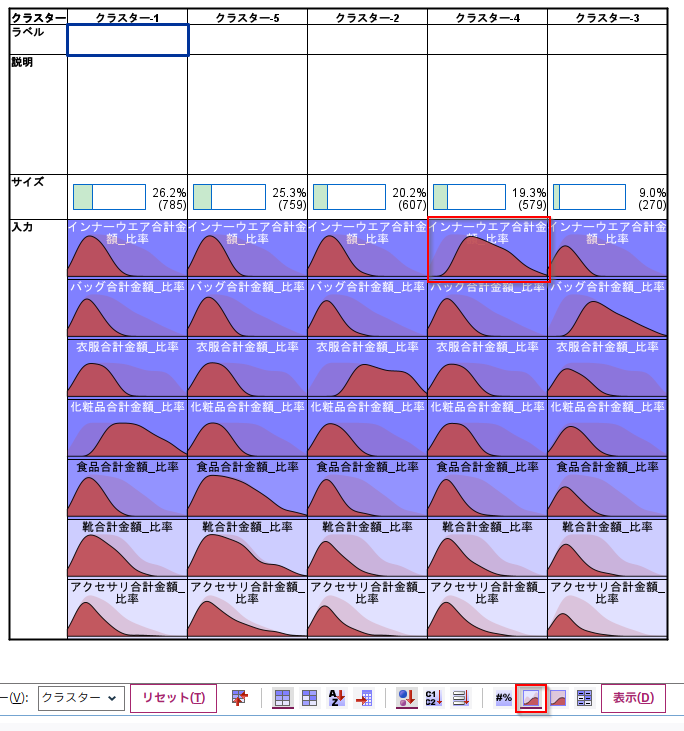
相対分布グラフ
クラスタービューの「相対分布」をみるとクラスター間での特徴をより強調して確認することができます。
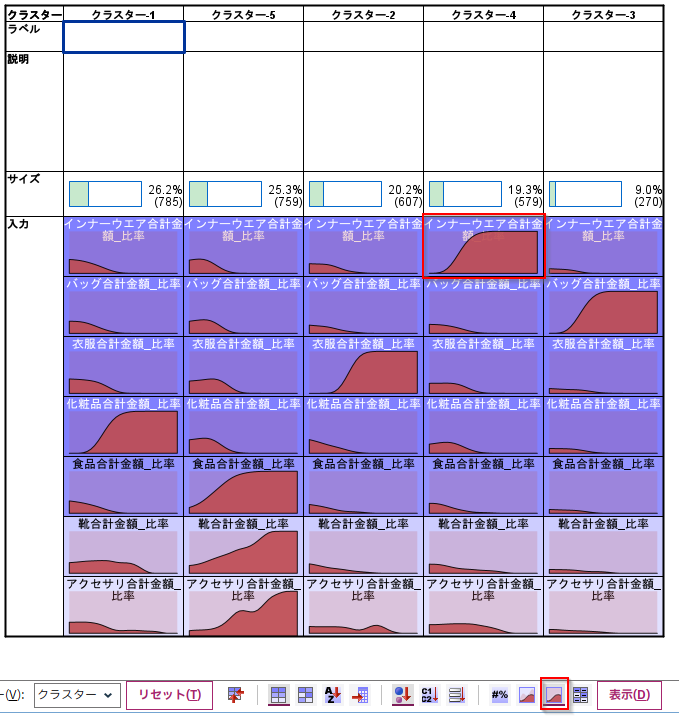
箱ひげ図
また、クラスタの比較の機能を使うと箱ひげ図で各クラスター間の値のばらつきも確認できます。
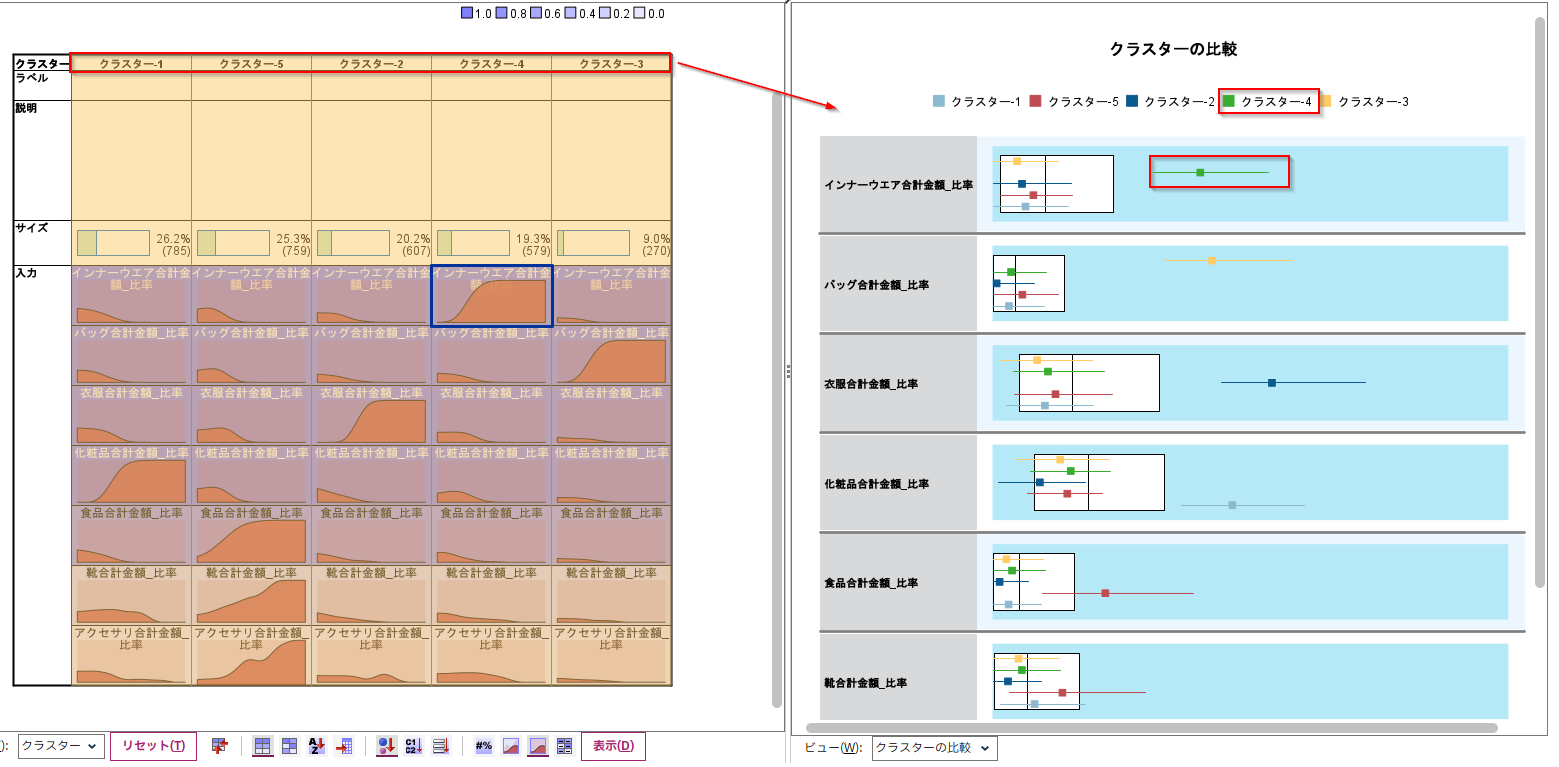
5p.クラスターの解釈 sklearn
専用のグラフなどは用意されていないのでmatplotlibなどで作る必要があります。
「絶対分布」のグラフを作ってみます。
クラスターサイズ・グラフ
まずクラスターサイズのグラフを作ります。
subplotsでncols=k分の列を作ります。
barhで各クラスター毎にdf_size.loc[j]['割合']のグラフを作ります。
fig, axes = plt.subplots(ncols=k, figsize=(
20, 1.5), sharex=True, constrained_layout=True)
fig.suptitle('サイズ')
for j in range(k):
axes[j].set_title("{:}: {:.2%}({:})".format(
j, df_size.loc[j]['割合'], df_size.loc[j]['度数']))
#横棒グラフ
axes[j].barh(y=[''], width=df_size.loc[j]['割合'])
axes[j].set_xlim([0, 1])
plt.show()
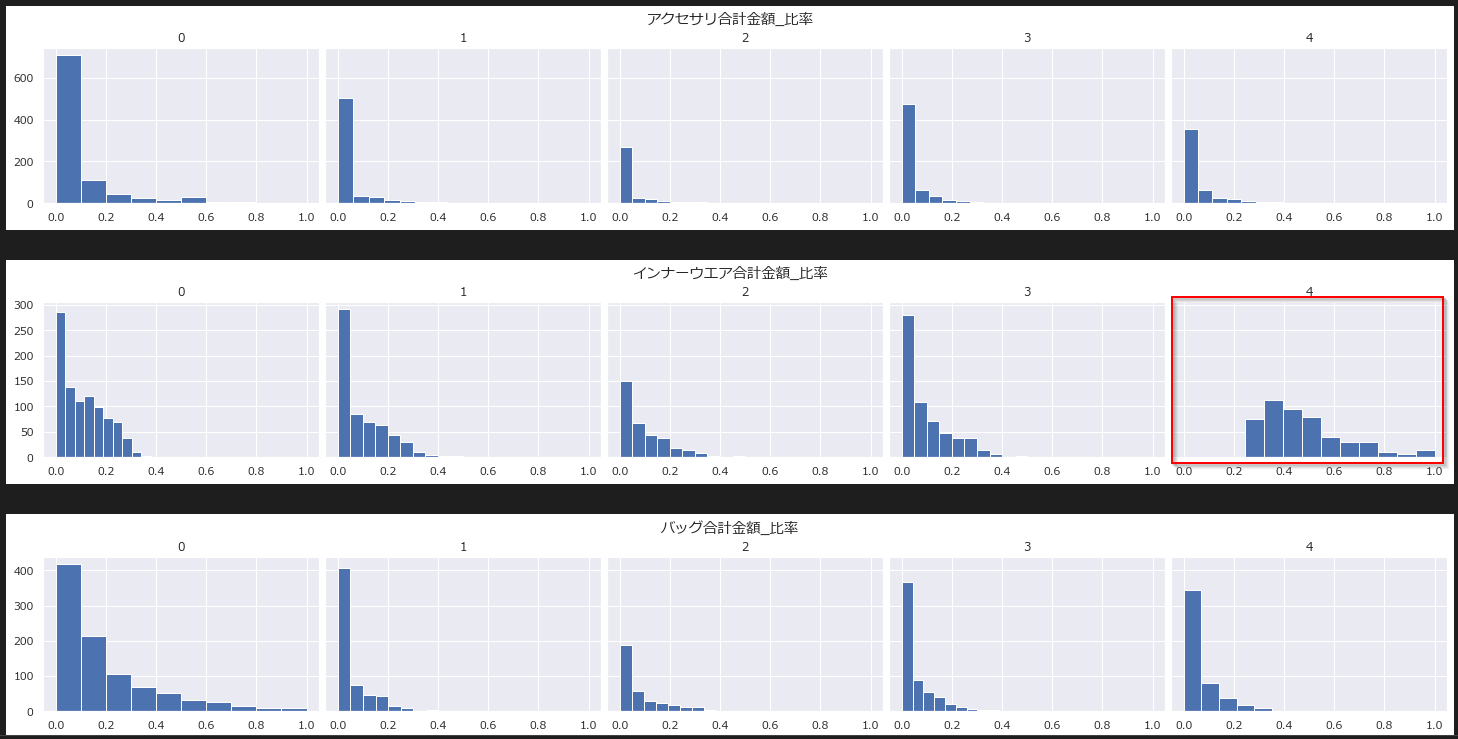
絶対分布グラフ
絶対分布を作ります。
subplotsでncols=k分の列を作ります。sharex=True, sharey=Trueでx,yの範囲を共通化します。
カテゴリ型は以下で棒グラフ化します。sort_indexを入れないと多い順になってしまいます。
df_km[df_km['$KM-K-Kmeans'] == j][col].value_counts().sort_index().plot.bar(ax=axes[j])
数値型は以下でヒストグラムを作ります。
axes[j].hist(data, bins=n_bins, label=col)
for i, col in enumerate(xlist):
fig, axes = plt.subplots(ncols=k, figsize=(
20, 3), sharex=True, sharey=True, constrained_layout=True)
fig.suptitle(col)
y_max = len(df_km[col])
for j in range(k):
axes[j].set_title(str(j))
#カテゴリ型は棒グラフ表示
if df_km[col].dtype.name == 'category':
df_km[df_km['$KM-K-Kmeans'] == j][col].value_counts().sort_index().plot.bar(ax=axes[j])
axes[j].set_ylim([0, y_max])
#数値型はヒストグラム表示
elif re.sub(r'[0-9]+', '', df_km[col].dtype.name) in ['int', 'float']:
data = df_km[df_km['$KM-K-Kmeans'] == j][col]
axes[j].hist(data, bins=n_bins, label=col)
クラスター4はインナーウェアの購入比率が高いことがわかります。
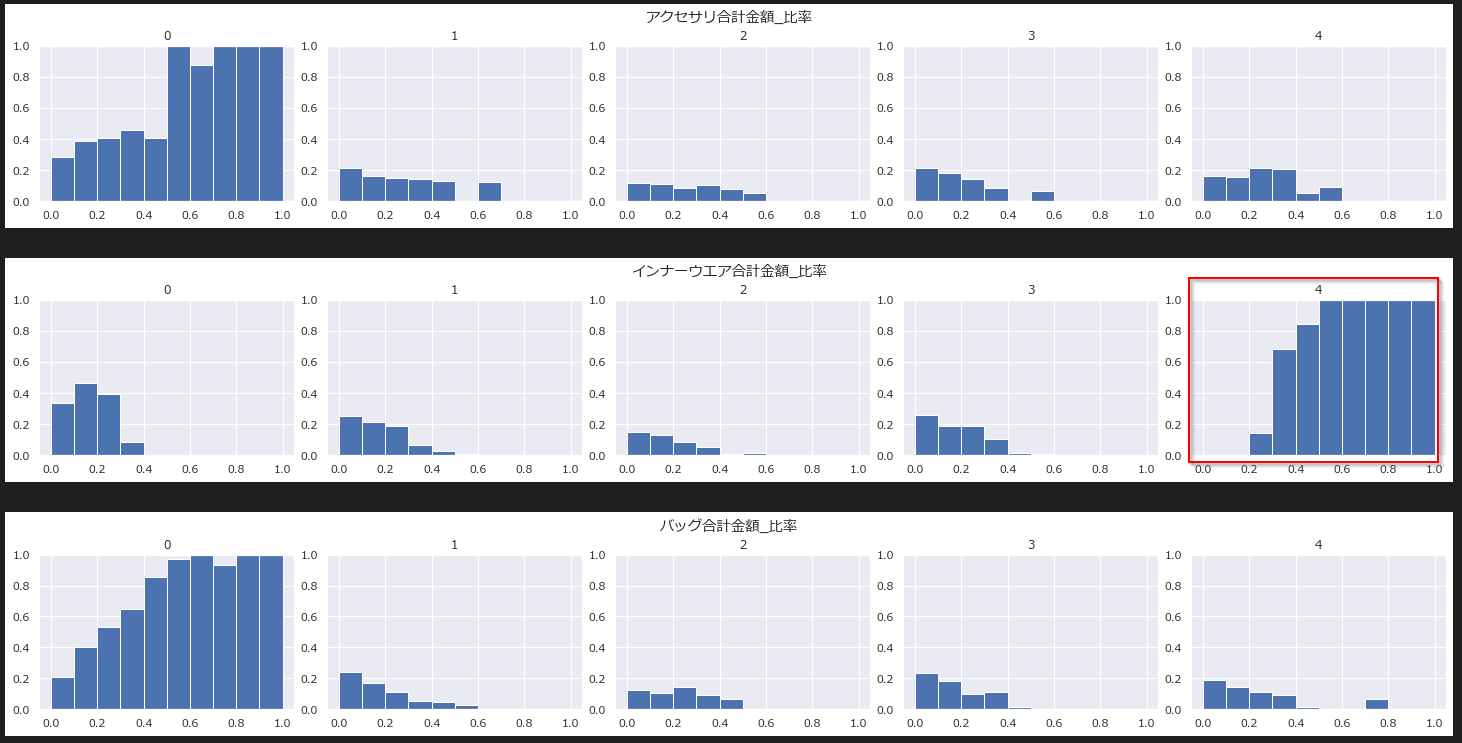
相対分布グラフ
相対分布を作ります。こういう相対度数のヒストグラムをつくるメソッドは用意されていなかったので、weightで、度数を調整する必要がありました。
まず、histでビニングせずに、その列内での全件をつかったビニングを行います。各クラスターに対して、histでビニングしてしまうとクラスター毎にビン間隔が変わってしまうのと、重みの計算ができないという問題があるためです。
df_tmp['bin'], fixed_bins = pd.cut(
df_km[col], n_bins, labels=False, retbins=True)
次に各ビンとクラスター毎の相対度数から重みを計算します。
例えば、50000円代というビンがあり、そのビンには全部で100名いて、クラスター1に10名、クラスター2に90名いたとすると、クラスター1は0.1、クラスター2は0.9の相対度数となります。これをさらに一人当たりのweightにするために、クラスター1は0.1/10、クラスター2は0.9/90として、一人一人に案分しています。
cluster_weights = df_tmp.groupby(['bin', '\$KM-K-Kmeans']).size()/df_tmp.groupby(
['bin']).size()/df_tmp.groupby(['bin', '\$KM-K-Kmeans']).size()
histでヒストグラムを作ります。全件をつかったビニングでつくったbinを指定し、各クラスター毎に割り振ったweightを指定しています。
axes[j].hist(data, bins=fixed_bins, label=col, weights=weights)
for i, col in enumerate(xlist):
y_max = len(df_km[col])
if re.sub(r'[0-9]+', '', df_km[col].dtype.name) in ['int', 'float']:
fig, axes = plt.subplots(ncols=k, figsize=(
20, 3), constrained_layout=True)
fig.suptitle(col)
df_tmp = df_km[['$KM-K-Kmeans', col]].copy()
#あらかじめ全件でのビニングを行う
df_tmp['bin'], fixed_bins = pd.cut(
df_km[col], n_bins, labels=False, retbins=True)
#各ビンに対するクラスターの相対度数を計算
cluster_weights = df_tmp.groupby(['bin', '$KM-K-Kmeans']).size()/df_tmp.groupby(
['bin']).size()/df_tmp.groupby(['bin', '$KM-K-Kmeans']).size()
cluster_weights.name = 'weight'
df_tmp = df_tmp.merge(cluster_weights, on=['bin', '$KM-K-Kmeans'])
for j in range(k):
axes[j].set_title(str(j))
data = df_tmp[df_tmp['$KM-K-Kmeans'] == j][col]
weights = df_tmp[df_tmp['$KM-K-Kmeans'] == j]['weight']
axes[j].hist(data, bins=fixed_bins, label=col, weights=weights)
axes[j].set_ylim([0, 1])
plt.show()
クラスター4はインナーウェアの購入比率が高いことがさらに強調されました。
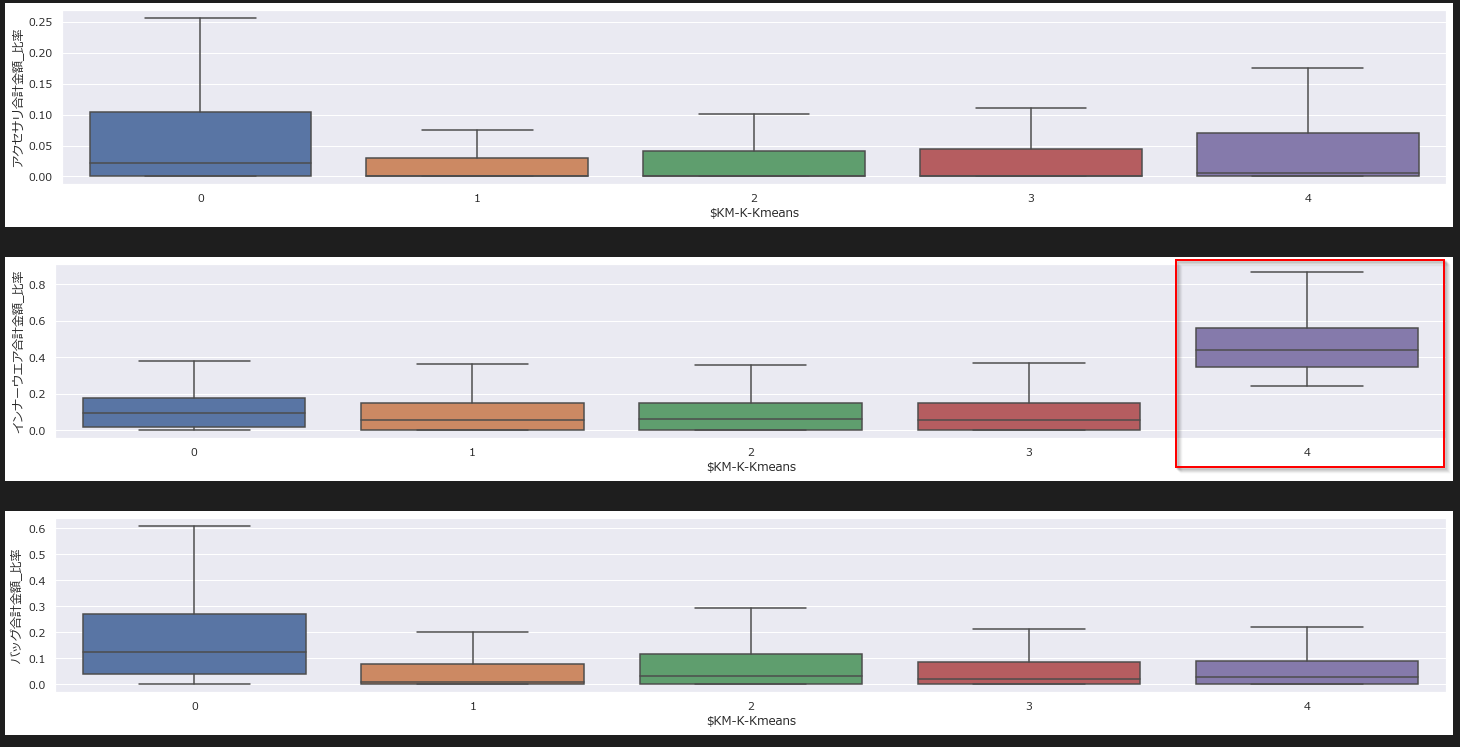
箱ひげ図
箱ひげ図で各クラスター間の値のばらつきを比較します。
seabornで書きました。
sns.set(font='Meiryo')
for i, col in enumerate(xlist):
#数値データは箱ひげ図で比較する
if re.sub(r'[0-9]+', '', df_km[col].dtype.name) in ['int', 'float']:
fig = plt.figure(figsize=(20, 3), constrained_layout=True)
ax = fig.add_subplot(1, 1, 1)
sns.boxplot(x='$KM-K-Kmeans', y=col,
data=df_km, showfliers=False, ax=ax)
plt.show()
箱ひげ図からもクラスター4はインナーウェアの購入比率が高いことがわかりました。
サンプル
サンプルは以下に置きました。
サンプルストリーム
notebook
利用データ
■テスト環境
Modeler 18.4
Windows 10 64bit
Python 3.8.10
pandas 1.4.1
sklearn 1.1.1