はじめに
全方位木DPは、ノード数$N$の木のすべてのノード$i$について$i$を根としたときに知りたい値を$O(N)$で求められるアルゴリズムです。何も知らないと$i$でループし、$i$を根とした場合の探索をして$O(N^2)$なので、全方位木DPによってとても速くなります。
ABC220のF問題を例にして、全方位木DPの気持ちを理解し、実際にACすることを確認します。
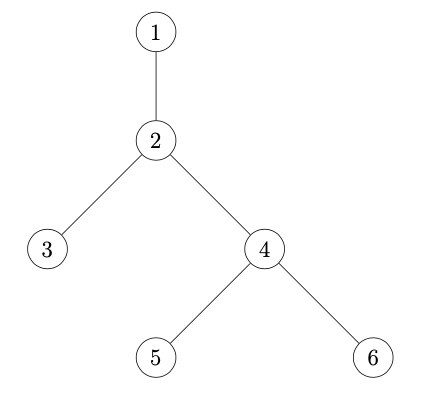
この記事では、以下の木を例にします。この木は、以下の入力に対応します。
6
1 2
2 3
2 4
4 5
4 6
また, 説明の際に以下の記号を用います。
- $p_i$: ノード$1$を根としたときの、ノード$i$の親ノード。例えばこの木では$p_4=2$
- $C_i$: ノード$1$を根としたときの、ノード$i$の子ノード集合。例えばこの木では$C_4=\{5, 6\}, C_5=\emptyset$
- $A_i$: ノード$i$に隣接するノードの集合。例えばこの木では$A_4=\{2, 5, 6\}$
- $T_i$: ノード$i$を根としたときの, ノード$i$の部分木に含まれるノード集合。例えばこの木では$T_2=\{2, 3, 4, 5, 6\}$
問題概要
$N$頂点の重みなし木が与えられます。頂点$i, j$間の距離を$dis(i, j)$とするとき, $i=1,\ldots,N$のそれぞれについて$\displaystyle \sum_{j=1}^ndis(i, j)$を出力せよ。
木DPについて
木DPは根を$r$に固定した木で、なんらかの配列$\text{dp}$の$i$番目の要素$\text{dp}_i$にノード$i$を根とする部分木の計算結果を保存していき、最終的に木全体($\text{dp}_r$の値)での値を求めます。
ここでは$r=1$として考えます。木DPを用いて、$\sum_{j=1}^ndis(1, j)$を求めます。($i=1$の場合に相当します。)
ここでは以下の2種類の値を求めていきます。(この理由は後ほど説明します。)
-
$\displaystyle\text{count}_i =\left|T_i\right|$: $i$を根とする部分木のノード数
-
$\displaystyle\text{dis_sum}_i=\sum_{j\in T_i}dis(i, j)$: $i$を根とする部分木の各ノード$j$について$dis(i, j)$を合計した値
$i=1$のとき、部分木が木全体になることから, $\text{dis_sum}_1$が求める値になることがわかります。
-
$i=3, 5, 6$のとき,
部分木はただ1つのノードなので、$\text{count}_i=1,\text{dis_sum}_i=0$です。$i$ $1$ $2$ $3$ $4$ $5$ $6$ $\text{count}_i$ $1$ $1$ $1$ $\text{dis_sum}_i$ $0$ $0$ $0$
-
$i=4$のとき,
部分木のノード数は, 子ノードの部分木のノード数の総和に1(自分自身)を加えた数になります。
$\text{count}_4=\text{count}_5+\text{count}_6+1=3$
また, 4以外のノードへは5または6を経由するので、4-5, 4-6の辺をノード数だけ通過し、それだけ$dis(i, j)$の総和も増加します。これが、$\text{count}_i$と$\text{dis_sum}_i$の2種類を計算する理由です。\begin{align*} \text{dis_sum}_4&=dis(4, 4) + \sum_{j\in T_5}dis(4, j) + \sum_{j\in T_6}dis(4, j)&\\ &=0+\sum_{j\in T_5}(1+dis(5, j)) + \sum_{j\in T_6}(1+dis(6, j))&\\ &=|T_5|+|T_6|+\sum_{j\in T_5}dis(5, j)+\sum_{j\in T_6}dis(6, j)&\\ &=\text{count}_5+\text{count}_6+\text{dis_sum}_5+\text{dis_sum}_6 \end{align*}$i$ $1$ $2$ $3$ $4$ $5$ $6$ $\text{count}_i$ $1$ $3$ $1$ $1$ $\text{dis_sum}_i$ $0$ $2$ $0$ $0$
-
$i=2, 1$のとき, 同様にして以下のように表が埋まります。
$i$ $1$ $2$ $3$ $4$ $5$ $6$ $\text{count}_i$ $6$ $5$ $1$ $3$ $1$ $1$ $\text{dis_sum}_i$ $11$ $6$ $0$ $2$ $0$ $0$
根を変更する
$i=1$のときの答えが出せました。ここから, $i=2,\ldots,n$のときの答えを求めます。
$i=2,\ldots,n$のときにはノード$i$には親$p_i$がいるので、これを利用します。
処理のイメージとしては以下の流れです。
- ノード$i$とノード$p_i$の間の辺を削除して、別々の木として計算する
- ノード$p_i$を$i$の子ノードに加えて再計算する
- 上記の1,2を親から順に行う
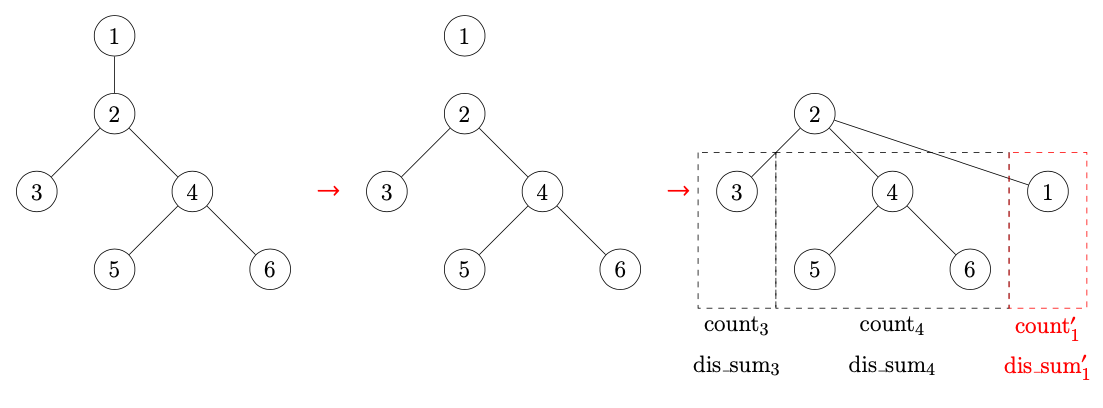
$i=2$のときの処理は以下のようになります。
もともと2の子ノードだった3, 4は最初に求めていたcount, dis_sumが使えますが、親ノードだった1については再計算が必要です。
ノード1を子ノードとして扱うには、1-2を結ぶ辺を削除しているので、
- $\displaystyle \text{count}'_1 = 1+\sum_{j\in A_1, j\ne 2}\text{count}_j$
- $\displaystyle \text{dis_sum}'_1 = \sum_{j\in A_1, j\ne 2}(\text{count}_j+\text{dis_sum}_j)$
が必要です。
ここでループして計算してしまうと全体で最悪$O(N^2)$になってしまうのですが、累積和のような方法を使うことで$O(N)$に抑えることができます。これで$i=2$での値がわかりました。
$i=2$の結果から同様にして$i=3, 4$の場合がわかり,$i=4$の結果から同様にして$i=5, 6$の結果がわかります。
全方位木DPまとめ(ABC220 F問題)
- 辺の情報を受け取って$A_i$, $p_i$, $C_i$を構築する。
- $p_i$は深さ優先探索などで求まる。
- $C_i$は$A_i - \{p_i\}$により求まる。
- 木DPで$i=1$のときの値を求める。
1.葉から順にループする。ノード$j$について、$\text{count}_j$, $\text{dis_sum}_j$を求める。- $\displaystyle \text{count}_j=1+\sum_{c\in C_j}\text{count}_c$
- $\displaystyle \text{dis_sum}_j=\sum_{c\in C_j}(\text{count}_c+\text{dis_sum}_c)$
- 根から順にループして、 $i=2,\ldots,N$のときの値を求める。
- $j\in A_i$のそれぞれについて、$\text{count}'_j$, $\text{dis_sum}'_j$を求める。
- $j\in C_i$のとき, $\text{count}'_j = \text{count}_j$, $\text{dis_sum}'_j=\text{dis_sum}_j$
- $j=p_i$のとき, $\displaystyle \text{count}'_j=1+\text{count_without}_j(i)$, $\text{dis_sum}'_j=\text{dis_sum_without}_j(i)$
- $\displaystyle \sum_{j\in A_i}(\text{count}'_j+\text{dis_sum}'_j)$が、求めたい値である。
- $j\in A_i$のそれぞれについて、$\displaystyle \text{count_without}_i(j)=\sum_{c\in A_i, c\ne j}\text{count}'_c$, $\displaystyle \text{dis_sum_without}_i(j)=\sum_{c\in A_i, c\ne j}\text{dis_sum}'_c$を求める。
- $j\in A_i$のそれぞれについて、$\text{count}'_j$, $\text{dis_sum}'_j$を求める。
全方位木DPまとめ(一般)
- 辺の情報を受け取って$A_i$, $p_i$, $C_i$を構築する。
- $p_i$は深さ優先探索などで求まる
- $C_i$は$A_i - \{p_i\}$により求まる
- 木DPで$i=1$のときの値を求める。
1.葉から順にループする。ノード$j$について、$\text{dp}_j$を求める。- $\displaystyle \text{dp}_j=f_{\text{after}}\left(\underset{c\in C_j}{F_{\text{merge}}}\bigl[f_{\text{before}}(\text{dp}_c, j, c)\bigr], j\right)$
- $f_{\text{before}}(\text{dp}_c,\text{parent}, \text{child})$:子ノードのdpの値を集約前に加工する関数。辺の情報を付加するときなど。
- $F_{\text{merge}}(v_1, v_2,\ldots)$:子ノードの情報を集約する関数。合計や最大など、結合側が成立する演算である必要がある。(モノイド)
- 単位元を$I$とする。
- $f_{\text{after}}(\text{merged},\text{node})$:集計後に加工する関数。ABC220Fでは$\text{count}_j$の総和をとったあとに1を加算したり, $\text{dis_sum}_j$に$\text{count}_j$を加算したりしている。
- 根から順にループして、 $i=2,\ldots,N$のときの値を求める。
-
$j\in A_i$のそれぞれについて、$\text{dp}'_j$を求める。
- $j\in C_i$のとき, $\text{dp}'_j = \text{dp}_j$
- $j=p_i$のとき, $\displaystyle \text{dp}'_j=\text{dp_without}_j(i)$
-
$\displaystyle f_{\text{after}}\left(\underset{c\in A_i}{F_{\text{merge}}}\bigl[f_{\text{before}}(\text{dp}'_c, i, c)\bigr], i\right)$が、求めたい値である。
-
$j\in A_i$のそれぞれについて、$\displaystyle \text{dp_without}_i(j)=f_{\text{after}}\left(\underset{c\in A_i, c\ne j}{F_{\text{merge}}}\bigl[f_{\text{before}}(\text{dp}'_c, i, c)\bigr], i\right)$を求める。
- $c\in A_i, c\ne j$は $c\in A_i, c < j$または $c\in A_i, j < c$なので,$j$未満で集約した値と, $j+1$以上で集約した値を集約します。
- 厳密には次の手順を行います。$A_i$を配列表現する。配列$\text{mf}, \text{ml}$を以下のようにして求める。(それぞれmerged_first, merged_lastの略です)
\begin{align*} \text{mf}[0] &= I,&\\ \text{mf}[k] &= F_{\text{merge}}\bigl( \text{mf}[k-1], f_{\text{before}}(\text{dp}'_{A_i[k]}, i, A_i[k])\bigr)\ \ (k=1,\ldots, |A_i|)&\\ \text{ml}[|A_i|+1] &= I,&\\ \text{ml}[k] &= F_{\text{merge}}\bigl( \text{ml}[k+1], f_{\text{before}}(\text{dp}'_{A_i[k]}, i, A_i[k])\bigr)\ \ (k=|A_i|,\ldots, 1)&\\ \end{align*}とすると,
\begin{align*} \text{mf}[k] &= \displaystyle \underset{0\leq m\leq k}{F_{\text{merge}}}\bigl[f_{\text{before}}(\text{dp}'_{A_i[m]}, i, A_i[m])\bigr]&\\ \text{ml}[k] &= \displaystyle \underset{k\leq m\leq |A_i|}{F_{\text{merge}}}\bigl[f_{\text{before}}(\text{dp}'_{A_i[m]}, i, A_i[m])\bigr] \end{align*}が保存される。$\displaystyle \underset{c\in A_i, c\ne A_i[k]}{F_{\text{merge}}}\bigl[f_{\text{before}}(\text{dp}'_c, i, c)\bigr]=F_{\text{merge}}\bigl(\text{mf}[k-1], \text{ml}[k+1]\bigr)$より、 $\text{dp_without}_i(j)$を求めます。
-