n番煎じではありますが、セグメント木をなんとなくわかった気になったので書いてみました。
セグメント木でできること
ある配列$A=A_1,A_2,...,A_n$に対する
- 区間の集計(最小値や総和など)
- 配列の値の更新
を高速に行うことができます。
セグメント木のデータ構造
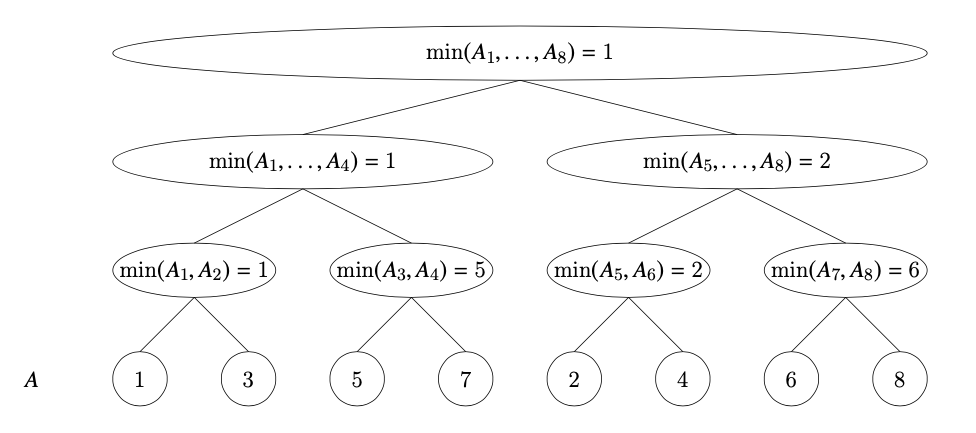
セグメント木は配列の要素を葉とする完全二分木です。親ノードが、子ノードの数値の集計結果を持っています。
例えば、$A=[1, 3, 5, 7, 2, 4, 6, 8]$に対する区間最小を扱うセグメント木は以下のようになります。
区間の集計結果を取得する
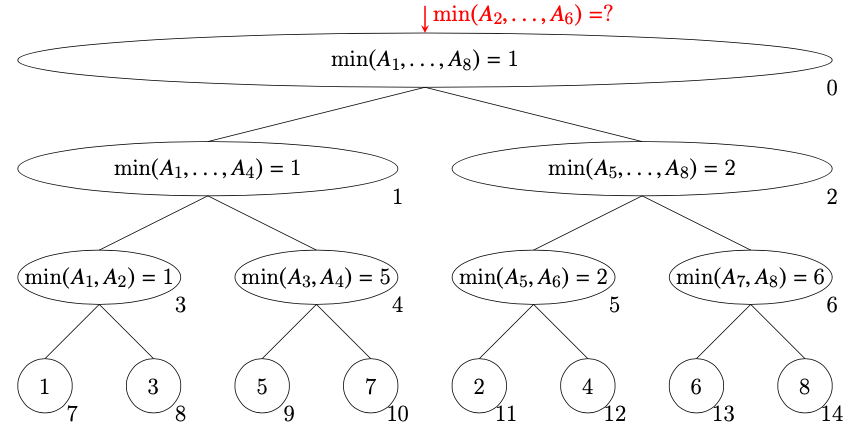
先ほどのセグメント木で、$\min(A_2, \ldots, A_6)$を求める場合は以下のようになります。各ノードの右下に番号を付しています。
-
ノード0は(自分が知っている最小値ではないので)ノード1に$\min(A_2,\ldots,A_4)$を、ノード2に$\min(A_5, A_6)$を質問する。
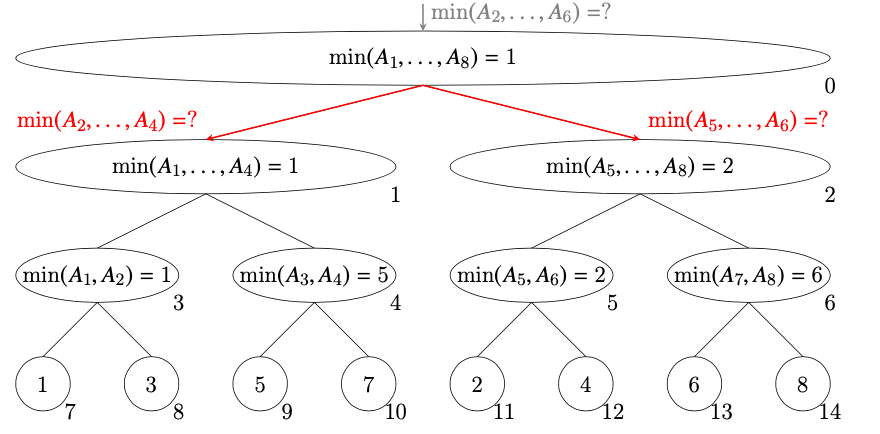
-
ノード1はノード3に$\min(A_2)$を、ノード4に$\min(A_3,A_4)$を質問する。ノード2はノード5に$\min(A_5, A_6)$を質問する。
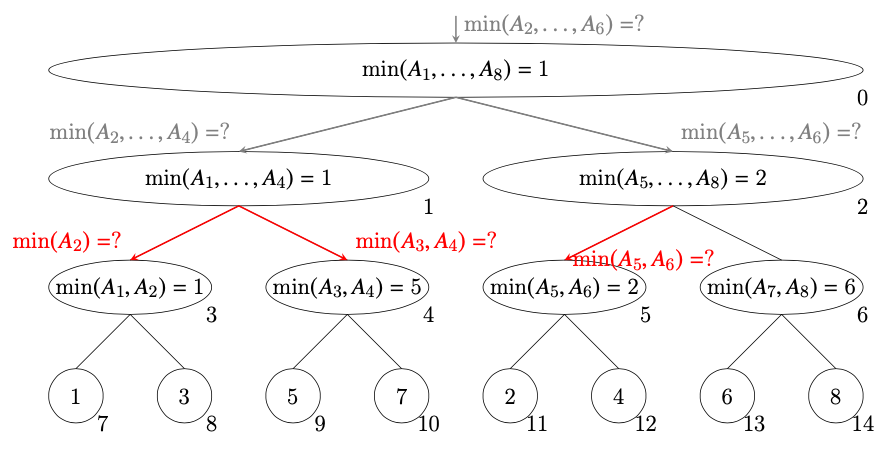
-
ノード3はノード8に$\min(A_2)$を質問する。ノード4とノード5は質問された区間と自分が知っている区間が同じなので、その値を答える。
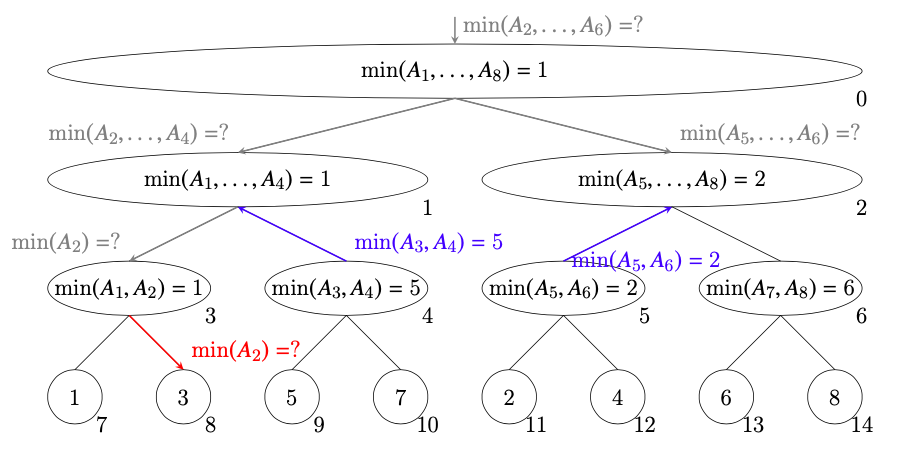
-
ノード8は$\min(A_2)=3$を答える。ノード8から答えを受け取ったノード3も$\min(A_2)=3$を答える。
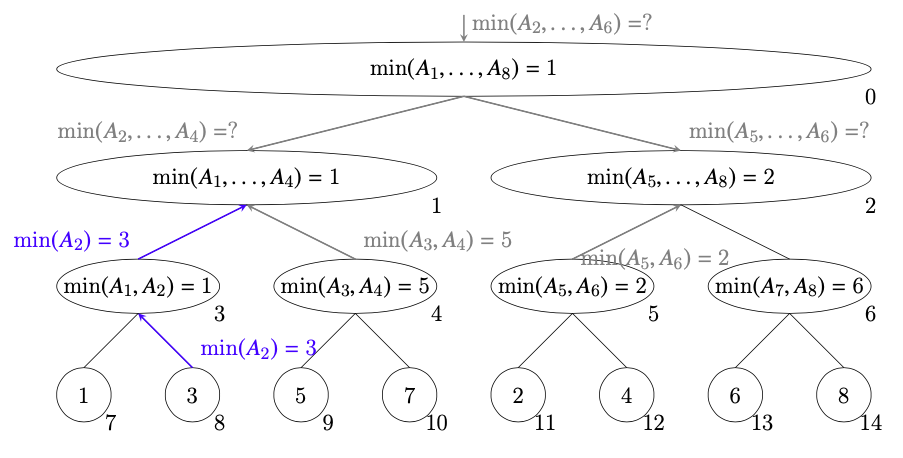
-
ノード1は$\min(A_2,\ldots,A_4)=\min(\min(A_2), \min(A_3, A_4))=\min(3, 5)=3$を答える。ノード2は子ノードから受け取った$\min(A_5,A_6)=2$を答える。
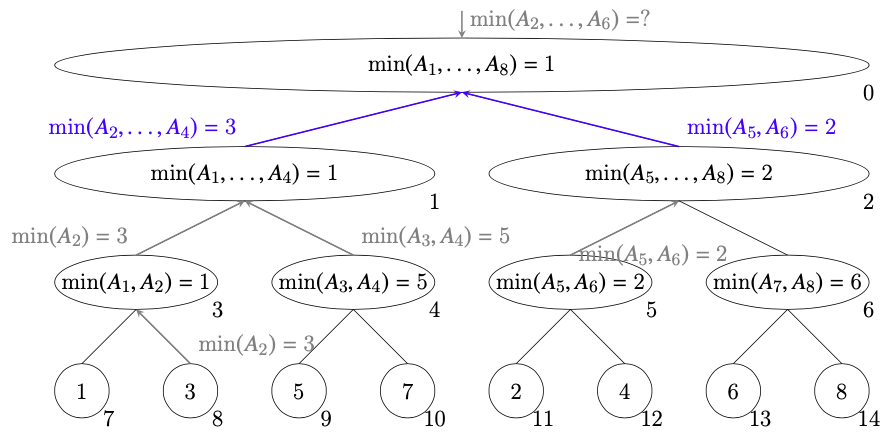
-
ノード0は$\min(A_2,\ldots,A_6)=\min(\min(A_2,\ldots,A_4), \min(A_5, A_6))=\min(3, 2)=2$を答える。
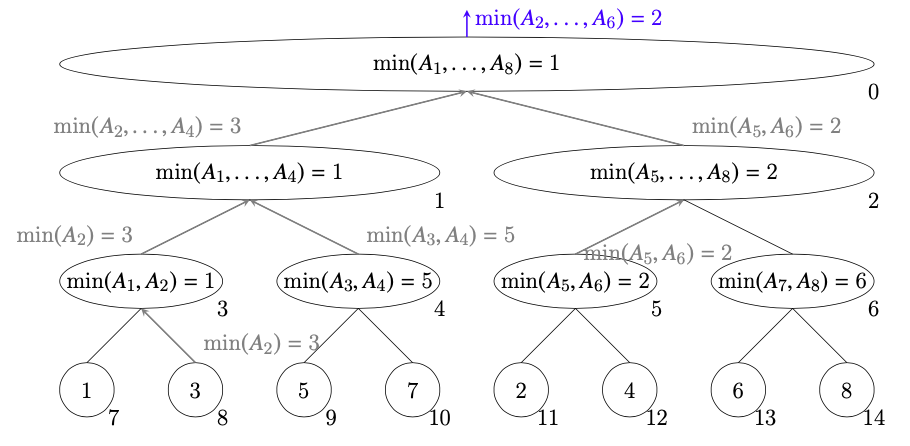
今回は要素数8の小さい配列で行ったのでわかりにくいのですが、同じ範囲のノードが見つかったらその子ノードについて計算する必要はないので、$O(\log(N))$で区間クエリを処理できます。
配列の値を更新する
区間の計算結果を冗長に管理しているので、配列の値を更新する場合は影響がある部分を再計算する必要があります。
影響がある部分は、その値が集計対象になっている部分、すなわち、更新対象の葉の先祖です。
$A_4=0$とする場合の更新処理は以下のようになります。(図を描くの疲れました。許して。)
- ノード10の値を0にする。
- ノード10の親であるノード4を再計算する。$\min(5, 0)=0$にする。
- ノード4の親であるノード1を再計算する。$\min(1, 0)=0$にする。
- ノード1の親であるノード0を再計算する。$\min(0, 2)=0$にする。
- ノード1は根ノードなので、終了する。
木の高さは$O(\log N)$なので、更新処理の計算量も$O(\log N)$になります。
集計できるもの
2つの区間の集計結果をまとめる性質上、集計する関数は結合法則が成り立つ必要があります。なので、2乗和を計算することはできません。(2乗した値を配列に入れて、その区間和を計算することで実現は可能です。)
また、例では配列の要素が$2^k$個ある場合で説明しましたが、それに満たない場合は単位元(演算に影響を与えない値)で埋める必要があります。加算を扱う場合は0、積を扱う場合は1、最小値を扱う場合は$\infty$(十分大きな値)で埋めたりしますが、実装の際はnullで埋めてしまえばいいと思います。(条件分岐は増えますが単位元を考える必要がなくなりますし、最大公約数などの単位元が存在しないものを扱えるようになります。)
参考文献
おまけ
最後に、自分がAtCoderでセグメント木を使うときに使いまわしているRustコードを貼り付けておきます。
#[derive(Debug)]
pub struct SegTree<T, F>
where
T: Clone,
F: Fn(T, T) -> T,
{
size: usize,
values: Vec<Option<T>>,
ranges: Vec<Option<(usize, usize)>>,
operator: F,
}
impl<T, F> SegTree<T, F>
where
T: Clone + Copy,
F: Fn(T, T) -> T,
{
pub fn new(values: Vec<T>, operator: F) -> Self {
let size = values.len();
let vals = vec![None; 2 * size.next_power_of_two() - 1];
let ranges = vec![None; 2 * size.next_power_of_two() - 1];
let mut seg_tree = Self {
size: size,
values: vals,
ranges: ranges,
operator: operator,
};
for i in 0..size {
let index_of_tree = seg_tree.index_of_tree(i);
seg_tree.values[index_of_tree] = Some(values[i]);
seg_tree.ranges[index_of_tree] = Some((i, i));
}
for i in (0..seg_tree.index_of_tree(0)).rev() {
// 降順に更新すれば順に値が求まる
let children_index = seg_tree.children_index(i).unwrap();
let v1 = seg_tree.values[children_index.0];
let v2 = seg_tree.values[children_index.1];
let val = seg_tree.eval(v1, v2);
let range = if seg_tree.ranges[children_index.0].is_none() {
None
} else {
let range_min = seg_tree.ranges[children_index.0].unwrap().0;
let range_max = if seg_tree.ranges[children_index.1].is_none() {
seg_tree.ranges[children_index.0].unwrap().1
} else {
seg_tree.ranges[children_index.1].unwrap().1
};
Some((range_min, range_max))
};
seg_tree.values[i] = val;
seg_tree.ranges[i] = range;
}
seg_tree
}
pub fn get(&self, index: usize) -> T {
let index = self.index_of_tree(index);
self.values[index].unwrap()
}
pub fn get_range(&self, left: usize, right: usize) -> T {
self.get_range_sub(left, right, 0).unwrap()
}
fn get_range_sub(&self, left: usize, right: usize, index: usize) -> Option<T> {
if self.ranges[index].is_none() {
// 指定されたindexに要素が存在しない
None
} else {
let current_range = self.ranges[index].unwrap();
if self.children_index(index).is_none() {
// 葉
if left <= current_range.0 && current_range.0 <= right {
self.values[index]
} else {
None
}
} else if left <= current_range.0 && current_range.1 <= right {
// 現在の範囲が覆われている場合
// 現在の範囲での値を返す
self.values[index]
} else if right < current_range.0 || current_range.1 < left {
// 現在の範囲と共通部分がない
None
} else {
// 現在の範囲と共通部分がある場合
// 子供も調べる
self.eval(
self.get_range_sub(left, right, self.children_index(index).unwrap().0),
self.get_range_sub(left, right, self.children_index(index).unwrap().1),
)
}
}
}
pub fn update(&mut self, index: usize, value: T) {
let mut index = self.index_of_tree(index);
self.values[index] = Some(value);
while !self.parent_index(index).is_none() {
index = self.parent_index(index).unwrap();
let children = self.children_index(index).unwrap();
self.values[index] = self.eval(self.values[children.0], self.values[children.1]);
}
}
fn eval(&self, v1: Option<T>, v2: Option<T>) -> Option<T> {
if v1.is_none() {
if v2.is_none() {
None
} else {
v2
}
} else {
if v2.is_none() {
v1
} else {
Some((self.operator)(v1.unwrap(), v2.unwrap()))
}
}
}
fn children_index(&self, index: usize) -> Option<(usize, usize)> {
if index > self.values.len() / 2 {
None
} else {
Some((2 * index + 1, 2 * index + 2))
}
}
fn parent_index(&self, index: usize) -> Option<usize> {
if index == 0 {
None
} else {
Some((index - 1) / 2)
}
}
fn index_of_tree(&self, index: usize) -> usize {
self.values.len() / 2 + index
}
}