遅延評価セグメント木も完全に理解する #競技プログラミング

この記事の続きです。

上記の記事で、

配列の1要素を更新する
区間の集計結果を取得する

が拘束にできるようになりました。これに加えて、

配列の区間のそれぞれの要素を更新する

もできるとこんな問題が解けて嬉しいです。

なので、遅延評価セグメント木をわかったつもりになります。

遅延評価セグメント木のお気持ち

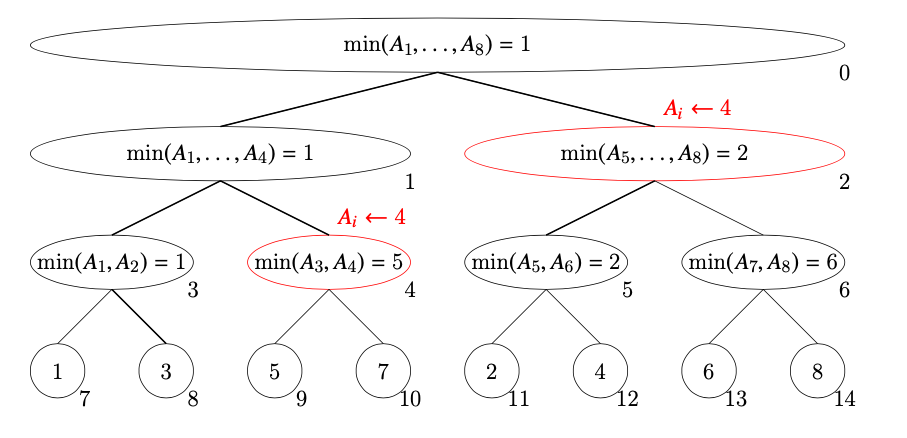
こちらの区間最小を計算するセグメント木に対して、次の操作をすることを考えます。

$a_i\leftarrow 4\ \ (3\leqq i\leqq 8)$ に更新
$\min(a_2, a_3, a_4, a_5)$ を取得

$a_i\leftarrow 4\ \ (3\leqq i\leqq 8)$ に更新
1. 区間取得と同様にして、$3\leqq i\leqq 8$に対応するノードを見つけます。見つけたノードに、遅延情報を入れます。
2. 見つけたノードの遅延情報を伝播します。伝搬とは、自身の値を更新し、遅延情報を子ノードに渡すことです。
3. 見つけたノードの先祖を更新します。今回は変わりませんでした。
$\min(a_2, a_3, a_4, a_5)$ を取得
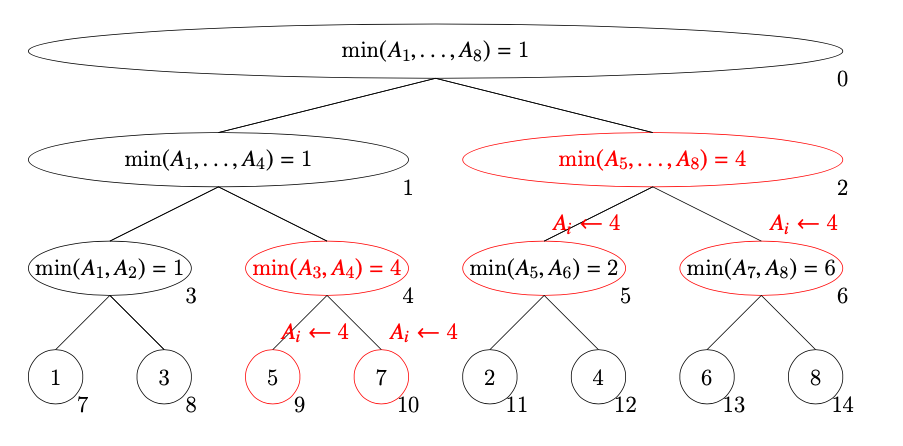
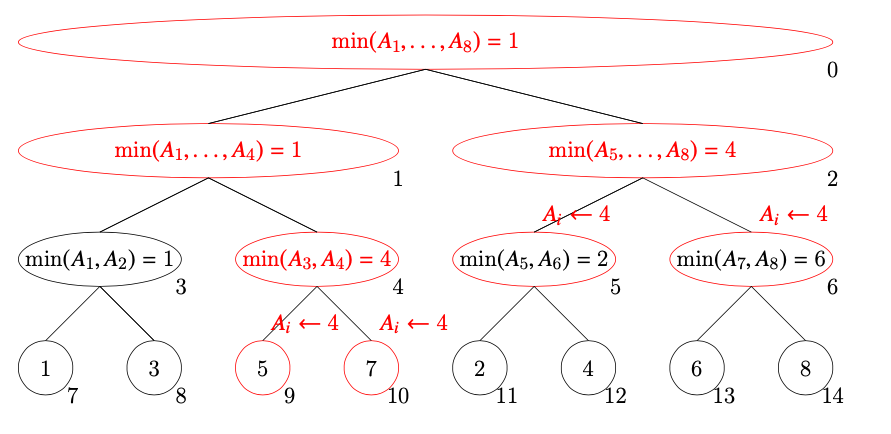
普通のセグメント木の流れに、「ノードにアクセスしたときに遅延情報を伝播する」処理が増えます。区間2,3,4,5に対応するノードは8番,4番,11番です。

8番
- 更新されたことがないので、そのまま3を返します。
4番
- 遅延情報を子ノードに伝播済みなので、そのまま4を返します。
11番
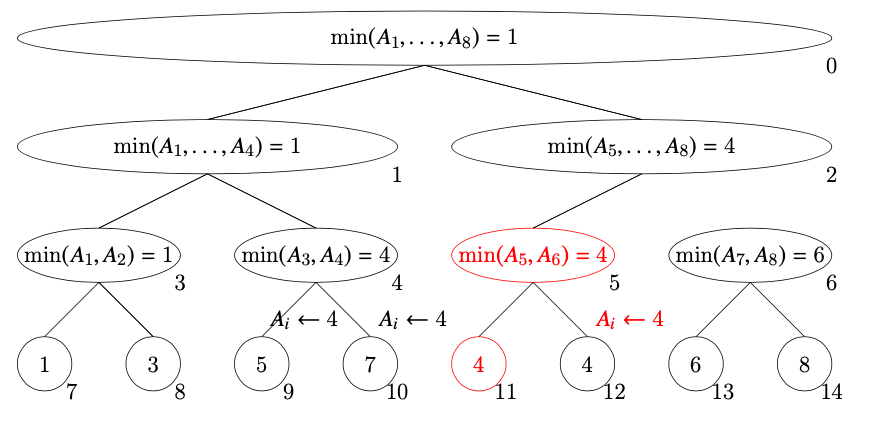
- 5番にアクセスしたときに、11番, 12番に遅延情報が伝搬されます。11番に遅延情報があるので、伝播して自分自身の値を4にします。その後、4を返します。

このようにして、最小値が3ということがわかりました。また、この取得の過程で一部の遅延情報が評価されたため、以下の赤い部分が更新されました。

遅延評価セグメント木に必要なもの

通常のセグメント木に必要なもの

操作対象の配列 $a=a_1,\ldots,a_n$
集計方法を表す二項演算 $\text{op}(a, b)$（$\min(a, b), a+b$など）
- 結合法則を満たしている必要あり
$\text{op}$ の単位元 $e$（最小値なら$\infty$, 和なら$0$など）

に加えて、以下が必要になります。

ノード $i$ の更新方法 $\text{mapping}(v', c, L)$
- $v'$: 更新前のノード $i$ の値
- $c$: 更新に使うパラメータ
- $L$: ノード $i$ がカバーする区間の長さ
- 更新結果のノード $i$ の値を返す
更新に使うパラメータの合成方法 $\text{composition}(c_\text{first}, c_\text{next})$
- $c_\text{first}$: 先に適用する更新のパラメータ
- $c_\text{next}$: 次に適用する更新のパラメータ
- $\text{mapping}(v', c, L)=\text{mapping}(\text{mapping}(v', c_\text{first}, L), c_\text{next}, L)$ を満たす $c$を返す

mapping の例

ノード $i$ が $\text{op}(a_l,\ldots,a_r)$を管理しているとします。

$a_i$の更新前の値を$a_i'$とします。すなわち、$v'=\text{op}(a_l',\ldots,a_r')$です。

$\text{op}=\min, a_i\leftarrow c$のとき
```
\begin{align*}
  \text{op}(a_l,\ldots, a_r)&= \min(a_l, \ldots, a_r)&\\
  &=\min(c, c, \ldots, c)&\\
  &= c
\end{align*}
```
これは更新前のノードの値 $v'$ や区間長 $L$ に依存しない例です。
この場合は$\text{mapping}(v', c, l)=c$となります。
$\text{op}=\text{add}, a_i\leftarrow a_i' \times c$ のとき
```
\begin{align*}
  \text{op}(a_l,\ldots, a_r)&= (a_l' \times c) + \cdots + (a_r' \times c)&\\
  &= (a_l'+\cdots+a_r') \times c
  &= v' \times c
\end{align*}
```
これは区間長 $L$ に依存しない例です。
この場合は$\text{mapping}(v', c, l)=v'\times c$ となります。
$\text{op}=\text{add}, a_i\leftarrow a_i' + c$ のとき
```
\begin{align*}
  \text{op}(a_l,\ldots, a_r)&= (a_l' + c) + \cdots + (a_r' + c)&\\
  &= (a_l'+\cdots+a_r') + (c + \cdots + c)&\\
  &= v' + c \times (r - l + 1)
\end{align*}
```
これは区間長 $L=l-r+1$ にも依存する例です。
この場合は$\text{mapping}(v', c, L)=v' + c \times L$となります。

公式ライブラリの使用例ではノードに乗せる構造体に区間長の情報を増やしています。
自分はこの遅延評価セグ木の配列の型を複雑にしたくなかったので、$\text{mapping}$の引数で区間長を受け取るようにしました。
https://atcoder.github.io/ac-library/production/document_ja/lazysegtree.html

composition について

ノードに設定する遅延評価のための更新情報が衝突することがあります。例えば、

$a_i\leftarrow a_i+1\ \ (1\leqq i \leqq 4)$
$a_i\leftarrow a_i+5\ \ (1\leqq i \leqq 4)$

のように、同じ区間に連続して更新クエリがやってくる場合です。これを都度伝搬させると結局更新が$O(N)$になってしまうので、

$a_i\leftarrow a_i+6\ \ $

として、1度の更新処理にまとめるのが$\text{composition}$の役割です。
上記の加算の例では、$\text{composition}(p_\text{first}, p_\text{next})=p_\text{first} + p_\text{next}$となります。

これは更新の順序によらない例ですが、

$a_i\leftarrow 1\ \ (1\leqq i \leqq 4)$
$a_i\leftarrow 5\ \ (1\leqq i \leqq 4)$

は更新の順序によって結果が変わる例です。

実装した

実際にACした回答がこちら（ネタバレ注意）