かつて統計を一生懸命勉強したladies & gentlemen
普段pythonとかRとかexcelとかmatlabとかがいい感じにしてくれるので、逆に基本的なことが飛んでいませんか。私は飛んでいます。ここでは一旦、忘れられがちな統計の概念を、今一度復習したいと思います。忘れたことすら忘れられた概念もあると思いますが、思い出したら追記します。
確率変数の定義ってなんだっけ？
確率変数 (stochastic variables)は、確率的に値が決まる変数のこと。試行をしないと値がわからない。
（例）サイコロが出る目は、$X = 1, 2, 3, 4, 5, 6$ の確率変数
中心極限定理ってなんだっけ？
中心極限定理 (Central limit theorem)は以下のように書ける。
ある母集団が平均$\mu$、分散$\sigma^{2}$の分布であるとする。正規分布でなくてもOK。そこから$N$個のサンプルを抽出する。この$N$が十分大きければ、標本平均の分布は、平均$\mu$、分散$\sigma^{2} / n$の正規分布 に近づく。
不偏分散ってなんだっけ？
標本分散 (sample variance)はこう。
\hat{\sigma}^{2} = \frac{1}{n}\Sigma_{i=1}^{n}(x_{i} - \bar{x})^{2}
$n$が小さいとその期待値が母分散の真値に一致しない（小さく見積もってしまう）。なので、不偏推定量にするため$n / n -1$をかける。
s^{2} = \frac{1}{n - 1}\Sigma_{i=1}^{n}(x_{i} - \bar{x})^{2}
これが不偏分散 (unbiased variance)。
母分散を推定したい時ってどうすればいいんだっけ？
不偏分散は母分散の推定値だが、「母分散の信頼区間を出してー」というとき、$\chi^{2}$分布を使う。
\frac{(n - 1)s^{2}}{\chi_{lower}^{2}} \sim \frac{(n - 1)s^{2}}{\chi_{upper}^{2}}
nは標本数、$s^{2}$は不偏分散、$\chi^{2}$はカイ二乗分布の下側と上側で、自由度$n-1$、％点が（95％信頼区間なら）下側は0.025、上側は0.975のものを選ぶ。
モーメント法ってなんだっけ？
点推定 (point estimate)で母集団の未知パラメータ$\theta$を推定したいときやり方は2つあり、フィッシャーの最尤推定法 (method of maximum likelihood)と、もう一つがモーメント法 (method of moments)だ。
ある母集団から抽出した$n$個のサンプル$X_{1}, X_{2}, ..., X_{n}$があるとすると、k次モーメントは以下のように書ける。
\hat{\mu_{k}} = \frac{X_{1}^{k} + X_{2}^{k} + ... + X_{n}^{k}}{n}
これだけだと何に使えるのか全くわからないが、これで母集団のパラメータを推定することができる。
例えば、1次モーメントは標本平均であり、母集団の平均の推定値とする（それでいいのか）。
母分散は、2次モーメントを用いて計算できる。過程は省くが、分散の定義式に2次と1次のモーメントを入れて計算するだけ。
\hat{\sigma}_{2} = \hat{\mu_{2}} - \hat{\mu_{1}}^{2}
これで母分散が推定できた。モーメント法が優れているのは、手で計算可能だということ。平均なら別だが、最尤推定手でやるのは辛い。
このようにして引き続き3次、4次のモーメントを用いると、skewness (左右対称性)やkurtosis（確率分布がどれだけとがってるか）も推定できる。
ところでSkewnessとkurtosisってなんだっけ？
Skewnessは歪度（わいど）と訳され、確率分布の左右対称性を表す。とーぜん、左右対称な正規分布では0になる。
kurtosisは尖度（せんど）と訳され、正規分布と比較したときの確率分布のとんがり具合を表す。公式は以下。
skewness = \frac{\Sigma_{i=n}^{n}(X_{i} - \bar{X})^{3} / n}{s^{3}}
kurtosis = \frac{\Sigma_{i=n}^{n}(X_{i} - \bar{X})^{4} / n}{s^{4}}
それぞれただの3乗、4乗なので、意外に簡単。これが元々の式だが、skewnessに関してはサンプルサイズ補正をするため前にn数をいじったものをかけた以下を使うことが多い。
skewness = \frac{\sqrt{n(n-1)}}{n - 2} \frac{\Sigma_{i=n}^{n}(X_{i} - \bar{X})^{3} / n}{s^{3}}
kurtosisに関しても、元の公式のままだと正規分布で計算したとき3になってしまうため、3を引いたものを使うことが多い。
kurtosis = \frac{\Sigma_{i=n}^{n}(X_{i} - \bar{X})^{4} / n}{s^{4}} - 3
仮説検定時に使うテストのパワーってなんだっけ？
仮説検定では否定したい帰無仮説 ($H_{0}$: null hypothesis)を立て、それを棄却することで対する対立仮説 ($H_{1}$: alternative hypothesis)が正しい、と主張しようとする。その際、なんらかの統計量（t値とか）を標本から計算し、結果がその確率分布のどこに位置するかによって$H_{0}$を受容するか棄却するか決める。
こういうまどろっこしいことをしているので、
「本当は$H_{0}$が正しかったけど、$H_{1}$が正しいって言っちゃった（ないのにあるって言っちゃった）」（Type I error; False positive; 偽陽性）
や
「本当は$H_{1}$が正しかったけど、$H_{0}$が正しいって言っちゃった（あるのにないって言っちゃった）」（Type II error; False negative; 偽陰性）
が起こりうる。以下の図は傑作。
すなわち、統計で言うパワー (statistical power; 検出力)とは、「あるときにあると言える」力のことで、
statistical power = 1 - 偽陰性となる確率
と定義される。
ちなみにfalse positiveとfalse alarmは同じ意味。
p-valueってなんだっけ？
もう一度言うぞ。
仮説検定では否定したい帰無仮説 ($H_{0}$: null hypothesis)を立て、それを棄却することで対する対立仮説 ($H_{1}$: alternative hypothesis)が正しい、と主張しようとする。その際、なんらかの統計量（t値とか）を標本から計算し、結果がその確率分布のどこに位置するかによって$H_{0}$を受容するか棄却するか決める。
計算したなんらかの統計量（t値とか）が、帰無仮説の元でその値になる確率がp値。
p < 0.05（あるいは0.01）なら帰無仮説が棄却され、対立仮説が採用される（慣習）。
効果量ってなんだっけ？
「老人と若者の英語テストの得点差は、p < 0.05で有意でした！」とは言っても、実際どの程度得点が違うのかは記述されるべき。
0.00000001点しか違わないなら、その有意差意味なくね？ってなるからだ。効果量 (effect size)はその名の通り、どの程度影響があったかを示したもの。例えば２群の比較だったら、平均の差を標準化したcohen's dが用いられることが多い。
cohen's \hspace{2mm}d = \frac{mean \hspace{2mm} difference}{pooled \hspace{2mm} standard \hspace{2mm} deviation}
この値が0.2以下だと効果は小さいし、0.8超えるとでっかいと言って良い（慣習）。
ところでPooled standard deviationって？
プールされた標本標準偏差のこと（いやそりゃわかる）。以下の式で計算できる。
pooled \hspace{2mm} standard \hspace{2mm} deviation = \sqrt{\frac{(n_{1}-1)s_{1}^{2}+(n_{2}-1)s_{2}^{2}}{n_{1} + n_{2} - 2}}
ここで$n$はそれぞれの群の標本数、$s^{2}$は不偏分散 ($n - 1$を使うやつ)。
線形回帰が使える時ときってどんなときだっけ？
線形回帰 (linear regression) は、目的変数$Y$ (dependent variable)を説明変数$X$ (independent variable)に係数$\beta$ (coefficient)をかけたものの線形和で説明する分析手法。
Y = X\beta + \epsilon
最後の$\epsilon$は誤差項。線形回帰は非常に汎用的だが、実は使用には５つの前提条件がある。
- Linear relationship ... $Y$は$X$は線形の関係にある
- Multivariate normality ... 全ての変数は（だいたい）正規分布に従う。正規分布に従うかのチェックはヒストグラムやQQplotを書いて確認する。
- No or little multicollinearity ... $X$内の説明変数同士の相関関係が無いか、あってもすごい小さい
No auto-correlation ... 目的変数$Y$に自己相関がない。（つまりxが時間なら、$y(x)$と$y(x+1)$は独立でないといけない）。言い換えると、残差同士が独立。
Homoscedasticity ... 等分散性のこと。残差 (residual = 予測と実測の差)の分散が一定で、$X$に依存しない。つまり以下の図（太線が回帰線、その周りの2つの細い線が残差が散らばっている範囲とする）の右の状況が望ましい。
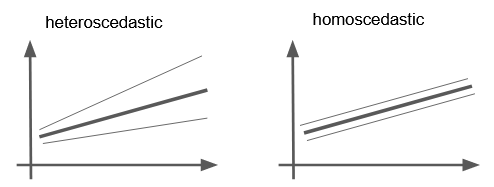
コメント欄でs_katagiriさんが詳しく解説してくださってるので参考に
相関係数と決定係数の違いってなんだっけ？
相関係数 (correlation coefficient)は、２つの変数の線形な関係の強さを定量する。相関があることは、因果関係を意味しない（これ大事！）。相関係数を計算するには、共分散$\sigma_{x, y}$を標準偏差$\sigma_{x}$、$\sigma_{y}$の積で割ればOK。
correlation \hspace{2mm} coefficient = \frac{\sigma_{xy}}{\sigma_{x}\sigma_{y}}
範囲は-1 ~ 1の間を取る。ちなみに共分散 (covariance)は、それぞれの平均からの偏差の平均。
covariance = E[(X - \bar{X})(Y - \bar{Y})]
決定係数 (coefficient of determination)は、線形モデル$f$において$X$がどれだけ$Y$を説明できたかを表す。
coefficient \hspace{2mm} of \hspace{2mm} determination = 1 - \frac{\Sigma_{i=1}^{n}(y_{i} - f(x_{i}))^{2}}{\Sigma_{i=1}^{n}(y_{i} - \bar{y})^{2}}
explained varianceと呼ばれることもあり、1に近ければ予測がよくできていたことを表す。あまりにも予測が悪いとマイナスになる。
最小二乗法 (least squared method)による線形回帰では、決定係数 = 相関係数の2乗になるため、相関係数が$R$とよく書かれるので、決定係数は$R^{2}$とよく書かれる（繰り返しだが、あまりにもモデルが悪いと2乗と書かれてはいてもマイナスになる）。
カイ二乗検定っていつ使うんだっけ？
主な使い方は2つ、「適合度の検定」と「独立性の検定」。そもそも$\chi^{2}$とは、それぞれの事象の頻度の観測値と理論値との差の二乗を、理論値で割ったものを足し合わせた統計量だ。すなわち、
\chi^{2} = \Sigma\frac{(O - E)^{2}}{E}
$O$は実測の頻度で、$E$は（帰無仮説の元での）期待される頻度を表す。
適合度の検定 (test of goodness of fit)では、観察された頻度と（帰無仮説において）予測される頻度、この2つの差が許容できるかどうか検定する。
例えばパーティを開催し100人来たとき、世間の男女比は1:1だから参加者は50人男性で50人女性だろうと期待されたが、実際は90人男性で10人女性だった場合、「あれ、このパーティの参加者って世間からランダムにサンプルされてる…？（帰無仮説）されてなくね...?（対立仮説）」という検定を$\chi^{2}$検定を用いて行うことが可能だ。
独立性の検定 (test of independence)はその応用で、クロス集計表から、縦の項目と横の項目は独立である、という帰無仮説を立て、その場合期待される頻度を計算したのち、適合度検定を行ってクロス集計表の縦横同士に関連があるか検定する。
例えば、そこらへんを歩いている人たちに「mac派かwin派か？」「エンジニアかそうじゃないか？」というアンケートを取り、2 x 2のクロス集計表にまとめる。このとき、「エンジニアであるかどうかは、OSの志向に関係がない」を帰無仮説として立てることができ、$\chi^{2}$検定で「エンジニアであること」と「OSの志向」が独立かどうか判定できる。
まとめのまとめ
$\chi^{2}$関連忘れがち…