[公式サイトより](http://www.madoka-magica.com/)
[公式サイトより](http://www.madoka-magica.com/)
エントロピー (entropy) は今日、アニメでも重要な概念になっています。
「あれ、エントロピーってなんだったっけ?」
という私のような人のために、情報理論におけるエントロピーの概念をざっくり復習したいと思います。
エントロピーとは、「予測できなさ」#
エントロピーとは、「予測できなさ」(Unpredictability) です。
例えば「今日は家にネギしかないし、買い出しは面倒だから外食しよう」と思ったとき、エントロピー的には自炊<外食となっています。自炊の場合、何を食べるかは完全に予測可能です(ネギです)。ところが外食の場合、牛丼、ラーメン、焼き肉、寿司などなど、何を食べるかの予測は難しいです。そのため、外食の方が情報量が多い、つまりエントロピーが大きくなります。
一般化すると、ある事象$X = X_1, X_2, ..., X_n$が起こる確率が、それぞれ$p = p_1, p_2, ..., p_n$ であるとすると、事象$X$ のエントロピー$H(X)$ は以下のように定義されます。
H(X) = - \sum^n_{i=1}p_i \log_2{p_i}
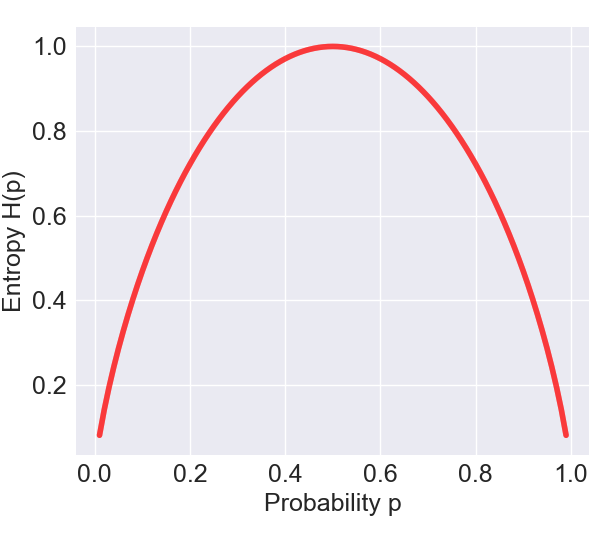
事象$X$ がベルヌーイ分布 (Bernoulli distribution)に従う、つまり、$X$ が起こる確率が$p$、起こらない確率が$1-p$ で、その試行が独立に繰り返されるとき、$p$ とエントロピー$H(X)$ の関係は以下のような有名な釣り鐘状のグラフを描きます。
エントロピーが最大になるのは$p=0.5$ のときですね。このときは$X$ が起こるのか、それとも起きないのか、全く予測ができない状態なので、エントロピーは最大になります。一方、$p=0.1$や$p=0.9$だと、$X$ が起こるか起きないか予測しやすいため、エントロピーは低くなります。
直感通り、一般的に、確率分布が一様分布 (Uniform distribution)に従うとき、エントロピーは最大になります。
エントロピーの簡単な導出#
一般ピープルが確率$p_i$ で起こる事象$X_i$の「予測できなさ」を定量しようとすれば、「起こりやすさ=予測しやすさ」が$p_i$ ということですから、逆数を取って$\frac{1}{p_i}$ とするでしょう。ところが、このエントロピーを提唱したシャノン (Claude Shannon)さんは今後の計算の利便性を考慮し、それの対数をとりました。
対数の利点は、確率分布の対数をとることで、各確率の逆数の積で表現されていた予測しにくさを、和の形で表現することができることにあります。つまり、全体の予測しにくさを、独立した各事象の予測しにくさの和の形(加算平均)として、簡単な計算で定量することができるのですね。(credit: termoshttさん)
ということで、$X_i$の予測しにくさ$H(X_i)$は、
H(X_i) = \log_2\frac{1}{p_i} = -\log_2{p_i}
そのため、$X = X_1, X_2, ..., X_n$ の予測しにくさ$H(X)$は、各事象の予測しにくさ$H(X_i)$の加重平均を取って、以下のように書けます。
$X$の予想しにくさ = $-p_1(\log_2{p_1}) -p_2(\log_2{p_2}) - ... - p_n (\log_2{p_n})$
つまり、
H(X) = - \sum^n_{i=1}p_i \log_2{p_i}
と、エントロピーの公式が導かれます。公式だけ見るとなんじゃこれはとなりますが、実際はただの予測しにくさの加重平均なのですね。
相互情報量#
そもそも我々はなぜ日夜インターネットに勤しんでいるのでしょうか。その答えは依存しているからこの世の中に対する「予測しにくさ」を、意味のある情報を得ることによってより「予測できる」ものにするためです。
このように、ある事象$Y$ を観測したのち、どれくらい事象$X$ に対する「予測しにくさ」が減少したかを表すのが、**相互情報量 (mutual information)**です。もちろん、考えたのはシャノンさんです。
相互情報量の定義には、$Y$を観測した後における$X$の予測しにくさ、すなわち**条件付きエントロピー$H(X|Y)$ (conditional entropy)**を求めることが必要です。そうすれば、$H(X) - H(X|Y)$で相互情報量が求められます。
どう求めるかというと、条件付き確率$P(x|y)$をそのまま、エントロピーの公式に突っ込みます。
H(X|Y) = \sum_y P(y)[-\sum_x P(x|y) \log_2{P(x|y)}]
今回は変数が$X,Y$と2つあるので、加重平均をそれぞれ行っているところに注意してください。
ところで、$y$のあとで$x$が起こる条件付き確率$P(x|y)$は、以下のように書けます。
P(x|y) = \frac{P(x \cap y)}{P(y)}
これを条件付きエントロピーの式に代入し、$H(X)$から引くと、相互情報量$I(X;Y)$を求める公式を導出できます。
I(X;Y) = H(X) - H(X|Y) = \sum_{x}\sum_{y}P(x \cap y)\log_2 \frac{P(x \cap y)}{P(x)P(y)}
相互情報量は必ず正の値を取り、その単位はビット (bits) と呼ばれます。相互情報量は$X$の予測しにくさが$Y$の観測によってどれだけ減少したかを示しますが、それは同時に、$Y$から$X$にどれだけの情報が流れたのかを定量していることになります。
まとめのまとめ#
- エントロピー (entropy) は、「予測しにくさ」。
- 相互情報量 (mutual information) は、ある事象を観測したとして、もう一つの事象に対する「予測しにくさ」がどれだけ減少したかを示す。
おまけのおまけ#
シャノンの発明品、その名もUltimate Machine!
コード###
本文中のグラフ、エントロピー vs 確率(ベルヌーイ試行)をプロットします。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Entropy as a function of probability --------
# random sample for probabilities
p = np.arange(0.01,1,0.01)
# compute binary entropy
entropy = -p*np.log2(p) - (1-p)*np.log2(1-p)
# visualize
plt.plot(p,entropy,linewidth=4,color='r',alpha=0.5)
plt.ylabel('Entropy H(p)', fontsize=18)
plt.xlabel('Probability p', fontsize=18)
plt.tick_params(labelsize=18)
plt.tight_layout()
参考###