世の中には様々な現象があふれています。それらを理解するということは、それらの挙動を説明するモデルを作ることであるといえます。そのモデルがある現象を観測したデータを予測できたなら、ある現象について理解したと言っていいでしょう。
モデルをデータにフィットする際、主に2つのやり方があります。
- 最小二乗法 (least squared method)
- 最尤推定法 (maximum likelihood method)
実際、どちらをどういうときに使えばいいのでしょうか。今回は簡単な例題を通して、**曲線近似 (curve fitting)**をやってみます。
課題
古典的な意識 (consciousness) の研究の例でやってみましょう。被験者にモニターの前に座ってもらい、モニター上に視覚刺激を提示します。視覚刺激はシグナル (signal)とノイズ(noise)が含まれており、被験者には、各トライアルごとに、シグナルが見えたかどうかを報告してもらいます。
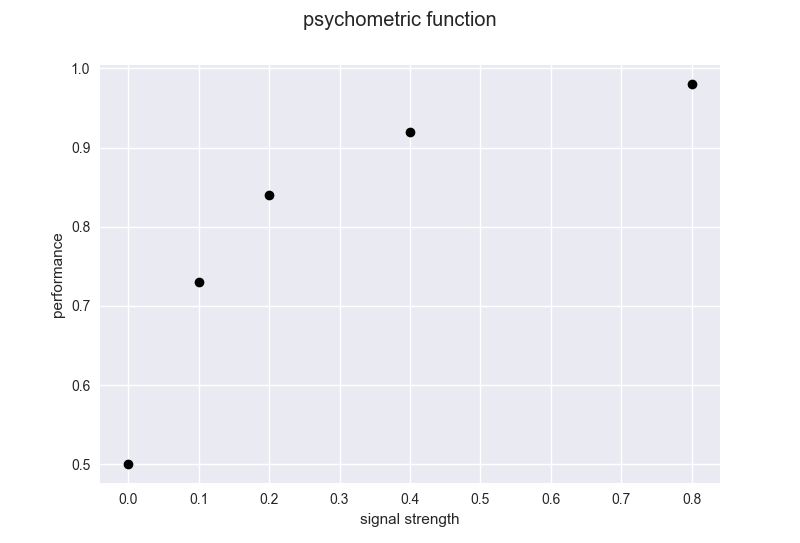
直感的に、シグナルの割合がノイズよりも大きいほど、検知 (detection)は簡単そうですよね。実際その通りで、シグナルの強さを横軸、被験者の検知パフォーマンスを縦軸にとると、例えば以下のようになります。
これを精神測定関数 (psychometric function)といいますが、今はそんなことはどうでもよくて、明らかに非線形 (non-linear) の関係が見て取れます。この非線形の関係を表すモデルを作り、データにフィッティングしてみましょう。それができれば、実験で使っていないシグナルの強さであっても、そのときの検知パフォーマンスを予測できます。それができれば、この非線形の現象を理解したことになります。
今回使用するデータを、以下にまとめます。
| signal | performance | number of trials |
|---|---|---|
| 0 | 0.5 | 50 |
| 0.1 | 0.73 | 45 |
| 0.2 | 0.84 | 40 |
| 0.4 | 0.92 | 35 |
| 0.8 | 0.98 | 30 |
被験者には全200トライアルやってもらったときの、各シグナル (signal) の強さに対応するパフォーマンス (performance) と、その刺激が登場した回数 (number of trials) が、フィッティングに必要な情報です。
今回はpythonを使うので、必要なライブラリをインポートして、データをリストに入れておきます。
# import libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import optimize
# experimental data ========
# signal strength
signal = [0, 0.1, 0.2, 0.4, 0.8]
# accuracy
accuracy = [0.5, 0.73, 0.84, 0.92, 0.98]
# number of trials
ntr = [50, 45, 40, 35, 30]
モデル
非線形のモデルは数多くありますが、例えば今回のような検知課題 (detection task)では**累積ワイブル (cumulative Weibull)**を使用するとうまくいくことがわかっています。
あるシグナルの強さ $s$ が刺激として提示されたとき、被験者が正答する確率 $p$ は、以下のようにあらわせます。
p = 0.5 + (0.5 - \lambda)f((\frac{s}{\theta})^\beta)
$f$は、$f(x) = (1 - e^{-x})$ です。 累積ワイブルの形を決定する自由パラメーター (free parameter)が3つ、$\lambda$, $\theta$, $\beta$とあります。実験でシグナルの強さ $s$ と被験者のパフォーマンス $p$ はわかっているので、これらをもとに、データにフィットする自由パラメーターを求めていくことになります。
実際のプログラミングにおいては、自由パラメーターは全て $x$ というリスト変数に入れます。$x[0] = \lambda$, $x[1] = \theta$, $x[2] = \beta$ というようにです。
# model for performance ========
def probabilityCorrect(x, signal):
# x: model parameters
# s: signal strength
# probability of correct
return 0.5 + (0.5 - x[0])*(1 - np.exp(-(signal/x[1])**x[2]))
モデルのフィッティング (最小二乗法)
まずは最小二乗法 (least squared method) を試してみましょう。最小二乗法は、一言で言うと**「モデルの予測値と実データの差が最小になる」** ような自由パラメーターを求める方法です。二乗を使うのは、単純に符号を考えなくて良くするためです。
自由パラメーターを求めるために、 損失関数 (cost function) というものを作ります。それをアルゴリズムに投げて、アルゴリズムにその損失関数が最小になるような自由パラメーターを見つけてもらう、という流れです。
最小二乗法では、損失関数はとても直感的です。モデルの予測値と、実データの二乗差を各シグナルの強さで計算して、足し合わせて1つの数値を出してくれるようにすればいいですね。
以下が実装例です。
def cost_LSE(x, signal, performance, ntr):
# compute cost
c = 0
for n in np.arange(len(ntr)):
# model output
p = probabilityCorrect(x, signal[n])
# cost as the summed squared error
c += ntr[n]*(performance[n] - p)**2
return c
損失関数ができたので、これをアルゴリズムに投げて最小値を取る自由パラメーターを探してもらいます。pythonでは、scipyにoptimizeというパッケージが入っているので、それを使います。
# initial guess and boundary
x0 = [0, 0.2, 1]
bound = [(0, None),(0.0001, None),(0,None)]
# least squared error
params_LSE = optimize.minimize(cost_LSE,x0,args=(signal,performance,ntr,),method='l-bfgs-b',\
jac=None, bounds=bound, tol=None, callback=None,\
options={'disp': None, 'maxls': 20, 'iprint': -1,\
'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000,\
'ftol': 2.220446049250313e-09, 'maxcor': 10,\
'maxfun': 15000})
引数がごちゃついてるかもしれませんが、基本的には公式サイトに載ってるデフォルトのコピペです。注意してほしいのは、自由パラメーター $x0$ の初期値を自分で決めなければいけないことです。
今回使うアルゴリズムはL-BFGS-Bというメモリーにも優しい汎用的なアルゴリズムですが、どのアルゴリズムであれ数値計算を繰り返して (numericalに) 最小値を探していくので、初期値が答えに近いことが理想です。初期値が見当違いの値だと、アルゴリズムの計算が収束しないこともあり、狙い通りのフィッティングができません。色々試すしかないですが、今回は経験的に「まぁこうなるんじゃね」という値を初期値にしています。
もう1つ、自由パラメーター$\lambda$, $\theta$, $\beta$ の範囲 (bound) をあらかじめ設定することができます。範囲を適切に設定することで、アルゴリズムは広大な数の海をさまよわずに済みます。今回は、どの自由パラメーターも正の値であり、かつ $x[1] = \theta$ はモデルの分母に来るために $0$ にはなってほしくない、ということで、上のように boundを設定しています。
これで、アルゴリズムL-BFGS-Bが損失関数を最小にする自由パラメーターの値を求めてくれます。
モデルのフィッティング (最尤推定法)
比較として、最尤推定法 (maximum likelihood method) を試してみましょう。最尤推定法は、一言で言うと**「ある自由パラメーターが与えられたときに、モデルが実データを予測する確率(尤度)を最大化する」** ような自由パラメーターを求める方法です。
実験をして、データをとりました。そのデータは、あるモデルの確率分布から来ていて、その確率分布は、モデルの自由パラメーターによって決まっている。なので、実データの値がモデルから出てくる確率(もっともらしさ、尤度、likelihoodを最大にするような自由パラメーターを求めましょう、という理屈です。
より具体的には、尤度は、各観測事象 $data_i$ がある自由パラメーター $x$ によってモデルに与えられる確率 $P(data_i | x)$ の同時確率 (joint probability) によって定義されます。高校で習ったように、各観察事象が独立して起こるとすると、同時確率は各事象が起こる確率の積であらわされます。
likelihood = P(data_0 | x)P(data_1 | x)P(data_2 | x)...P(data_n | x)
これを最大化するような関数を作りたいわけですが、自由パラメーターを求めるためには、アルゴリズムによって最小値を求められる損失関数 (cost function) を作るしかありません。ただ、今回は最大値が欲しいので、likelihoodにマイナスの符号をつけたものをアルゴリズムに渡します。
もう1つ、likelihoodはたくさんの確率の積なので、観測数が多いと値は限りなく0に漸近し、アルゴリズムが最大値を求めにくくなります。そのため、対数 (log)をとるという数学的トリックを使います。高校で習ったように、logをとることで、要素の積は要素の和に変換できるのですね。
結果として、最尤推定法でアルゴリズムに投げる損失関数は、logをとってマイナスをつけた、以下のようなものになります。
- log(likelihood) = - (log(P(data_0 | x)) + log(P(data_1 | x)) + log(P(data_2 | x)) ... + log(P(data_n | x))
以下が実装例です。
def cost_MLE(x, signal, performance, ntr):
# compute cost
c = 0
for n in np.arange(len(ntr)):
# model output
p = probabilityCorrect(x, signal[n])
# cost as the negative likelihood
if 0 < p <= 1:
c += -ntr[n]*(performance[n]*np.log(p) + (1 - performance[n])*np.log(1 - p))
return c
logを取る都合上、モデルの予測値は正の値でなければなりません。また、確率なので1より大きくならない。この2つの条件を $if$ のところに入れています。今回の例では、被験者が正答する確率を $p$ としてモデルしているので、被験者が正答しない確率は $1-p$ であることに注意してください。
損失関数ができたので、これをアルゴリズムに投げます。
# initial guess and boundary
x0 = [0, 0.2, 1]
bound = [(0, None),(0.0001, None),(0,None)]
# maximum likelihood
params_MLE = optimize.minimize(cost_MLE,x0,args=(signal,performance,ntr,),method='l-bfgs-b',\
jac=None, bounds=bound, tol=None, callback=None,\
options={'disp': None, 'maxls': 20, 'iprint': -1,\
'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000,\
'ftol': 2.220446049250313e-09, 'maxcor': 10,\
'maxfun': 15000})
フィッティング結果の比較
フィッティングの結果はどうでしょうか。グラフにしてみましょう。
# visualize
signals = np.linspace(0,0.8,100)
acc_mle = np.zeros(100)
acc_lse = np.zeros(100)
for i in np.arange(100):
acc_mle[i] = probabilityCorrect(params_MLE.x,signals[i])
acc_lse[i] = probabilityCorrect(params_LSE.x,signals[i])
fig = plt.figure()
fig.suptitle('psychometric function')
ax = fig.add_subplot(111)
ax.set_xlabel('signal strength')
ax.set_ylabel('performance')
plt.plot(signal, performance, 'ko')
plt.plot(signals, acc_mle, '-b')
plt.plot(signals, acc_lse, '-r')
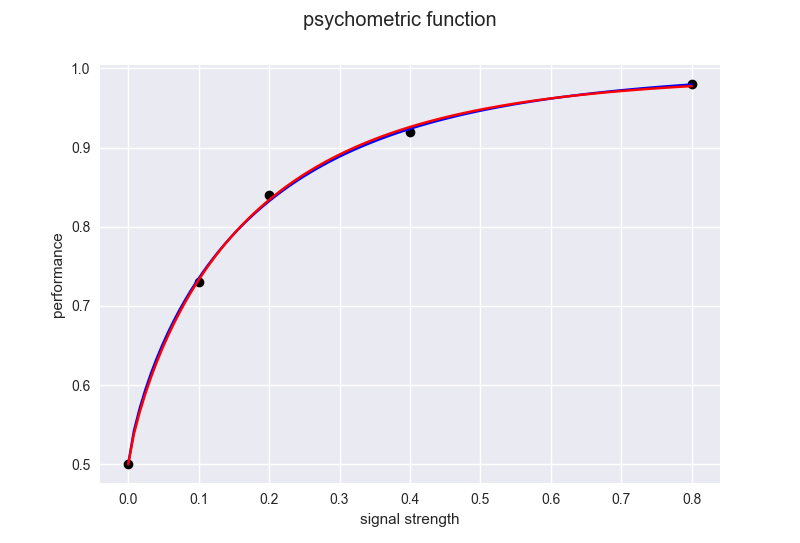
最小二乗法で得られたフィッティングを赤、最尤推定法で得られたフィッティングを青でプロットします。
……ほぼ違いないですねw どちらも綺麗にフィッティングできています。
実際、どれだけフィッティングがうまくいっているのか、variance explained という指標で数値化することができます。以下が公式になります。
varianceExplained = 1 - var(data - prediction)/var(data)
実データのバラツキを、予測値のバラツキがどれだけ説明したかを定量しています。これを計算してみましょう。
# compute variance explained
fitted_acc_mle = np.zeros(len(signal))
fitted_acc_lse = np.zeros(len(signal))
for s in np.arange(len(signal)):
fitted_acc_mle[s] = probabilityCorrect(params_MLE.x,signal[s])
fitted_acc_lse[s] = probabilityCorrect(params_LSE.x,signal[s])
varexp_mle = 1 - (np.var(fitted_acc_mle - performance)/np.var(performance))
varexp_lse = 1 - (np.var(fitted_acc_lse - performance)/np.var(performance))
print('variance explained (MLE): ' + str(varexp_mle))
print('variance explained (LSE): ' + str(varexp_lse))
計算の結果、
variance explained (MLE): 0.999339315626
variance explained (LSE): 0.999394193462
となりました。最小二乗法の方がちょーーーっとだけいいようですが、差は無視できるレベルでしょう。
とりあえず両方試してみて、よりフィットする方を選ぶといいかもしれません。
まとめのまとめ
- モデルのフィッティングには、最小二乗法か最尤推定法を用いる。
- モデルを作る、損失関数を作る、最小値を求めるアルゴリズムに投げる、の流れ。
- フィッティングの良し悪しは、variance explained で計算できる。
終わりに
モデリング (modeling)は、機械学習など様々な分野で必須の考え方です。流れは決まっているので、最初は難しく見えても、自分でやってみると意外とすぐなじめるかもしれません。モデリングしてみたいけど、ちょっと怖い、そうした人たちの一助になれば幸いです。ソースコードを以下に載せておきます。
# -*- coding: utf-8 -*-
# import libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import optimize
# model for performance ========
def probabilityCorrect(x, signal):
# x: model parameters
# s: signal strength
# probability of correct
return 0.5 + (0.5 - x[0])*(1 - np.exp(-(signal/x[1])**x[2]))
def cost_MLE(x, signal, performance, ntr):
# compute cost
c = 0
for n in np.arange(len(ntr)):
# model output
p = probabilityCorrect(x, signal[n])
# cost as the negative likelihood
if 0 < p <= 1:
c += -ntr[n]*(performance[n]*np.log(p) + (1 - performance[n])*np.log(1 - p))
return c
def cost_LSE(x, signal, performance, ntr):
# compute cost
c = 0
for n in np.arange(len(ntr)):
# model output
p = probabilityCorrect(x, signal[n])
# cost as the summed squared error
c += ntr[n]*(performance[n] - p)**2
return c
# signal strength
signal = [0, 0.1, 0.2, 0.4, 0.8]
# performance
performance = [0.5, 0.73, 0.84, 0.92, 0.98]
# number of trials
ntr = [50, 45, 40, 35, 30]
# initial guess and boundary
x0 = [0, 0.2, 1]
bound = [(0, None),(0.0001, None),(0,None)]
# maximum likelihood
params_MLE = optimize.minimize(cost_MLE,x0,args=(signal,performance,ntr,),method='l-bfgs-b',\
jac=None, bounds=bound, tol=None, callback=None,\
options={'disp': None, 'maxls': 20, 'iprint': -1,\
'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000,\
'ftol': 2.220446049250313e-09, 'maxcor': 10,\
'maxfun': 15000})
# least squared error
params_LSE = optimize.minimize(cost_LSE,x0,args=(signal,performance,ntr,),method='l-bfgs-b',\
jac=None, bounds=bound, tol=None, callback=None,\
options={'disp': None, 'maxls': 20, 'iprint': -1,\
'gtol': 1e-05, 'eps': 1e-08, 'maxiter': 15000,\
'ftol': 2.220446049250313e-09, 'maxcor': 10,\
'maxfun': 15000})
# compute variance explained
fitted_acc_mle = np.zeros(len(signal))
fitted_acc_lse = np.zeros(len(signal))
for s in np.arange(len(signal)):
fitted_acc_mle[s] = probabilityCorrect(params_MLE.x,signal[s])
fitted_acc_lse[s] = probabilityCorrect(params_LSE.x,signal[s])
varexp_mle = 1 - (np.var(fitted_acc_mle - performance)/np.var(performance))
varexp_lse = 1 - (np.var(fitted_acc_lse - performance)/np.var(performance))
print('variance explained (MLE): ' + str(varexp_mle))
print('variance explained (LSE): ' + str(varexp_lse))
# visualize
signals = np.linspace(0,0.8,100)
acc_mle = np.zeros(100)
acc_lse = np.zeros(100)
for i in np.arange(100):
acc_mle[i] = probabilityCorrect(params_MLE.x,signals[i])
acc_lse[i] = probabilityCorrect(params_LSE.x,signals[i])
fig = plt.figure()
fig.suptitle('psychometric function')
ax = fig.add_subplot(111)
ax.set_xlabel('signal strength')
ax.set_ylabel('performance')
plt.plot(signal, performance, 'ko')
plt.plot(signals, acc_mle, '-b')
plt.plot(signals, acc_lse, '-r')