**信頼区間 (Confidence interval)は、統計学を習う際、最初の方に出てくる概念ですが、名前もあってその解釈にはしばしば誤解が生じます。直感的な解釈はベイズ統計学を用いた確信区間 (Credible interval)**の方がふさわしいのですが、その違いがわからない、そもそも確信区間とか知らない、という人も多いのではないでしょうか。
この記事では、統計学を2分する頻度論者 (Frequentist) とベイジアン (Bayesian) の立場を今一度明らかにし、信頼区間と確信区間の違いを理解し、データの統計学的解析に役立てたいと思います。
正しい信頼区間 (Confidence interval) の考え方##
データのバラツキを表現する方法は、分散 (Variance)、標準偏差 (Standard deviation)など様々あり、信頼区間 (Confidence interval) もその1つです。
$n$ 個のデータ$X$ から計算された興味あるパラメーター$\theta$ の信頼区間は、そのパラメーターが属する母集団の標準偏差$\sigma$ を用いて、以下のように計算されます。
(\theta - z\frac{\sigma}{\sqrt{n}},\hspace{5pt} \theta + z\frac{\sigma}{\sqrt{n}})
このとき、$z$ は信頼レベルを表し、両側95%なら標準正規分布の95%のデータが含まれる範囲である$z = 1.96$ を用います。多くの場合、母集団の標準偏差は知りえないことが多いので、**「正規分布の母集団のバラツキがわからないときは、母集団の標準偏差$\sigma$ の代わりに標本標準偏差$s$ を使い、パラメーターの分布はt分布に従うとする」**という統計学のテクニックを用います。このとき、信頼区間の計算式は以下のように書き換えられます。
(\theta - t\frac{s}{\sqrt{n}},\hspace{5pt} \theta + t\frac{s}{\sqrt{n}})
このとき、$t$ は自由度$n-1$、$\alpha = (1 - C)/2$ のt値です。$C$ は例えば95%信頼区間を求めたいなら、$C = 0.95$ なので、$\alpha = 0.025$ ですね。
この信頼区間、頻度論者 (Frequentist) の考え方なのですが、名前のおかげで以下のようなベイジアン (Bayesian) 的解釈をしてしまう間違いが多く見られます。
「信頼区間?例えば95%信頼区間だったら、得られたデータの95%がその範囲に入る、ってことでしょ?」
「信頼区間?例えば95%信頼区間だったら、得られたデータから計算された興味のあるパラメーターのばらつく範囲のうち、95%の範囲を示してるんでしょ?」
「信頼区間?例えば95%信頼区間だったら、実験を何度も繰り返したとき、95%の確率で興味のあるパラメーターがその範囲に入る、ってことでしょ?」
……残念ながら、全部違うのです。
95%信頼区間とは、実験をたくさん、例えば100回繰り返したとき、それぞれの実験で得られたデータから計算された興味あるパラメーターが、その信頼区間に収まっている実験の頻度が、95回である、ということを意味しています。
信頼区間という名前から直感的に考えてしまいがちですが、実はこれ結構解釈が難しい概念なんです。上記の定義を読んで「あぁなるほど!」とすぐ理解できる人はあまりいないのではないでしょうか。
なぜかというと、頻度論者は以下のように考えるからです。
「興味あるパラメーターには真の値が存在する」
「そのパラメーターの真の値は、母集団からやってくる」
「しかし、実験で得られるのは母集団の一部でしかない」
「そのため、各実験で計算されたパラメーターは、ある信頼区間に収まることも、収まらないこともある」
つまり、パラメーターの値は本来1つだけれど、実験を繰り返すことで生まれるバラツキの範囲をなんとか定量しよう、というのが信頼区間の哲学なのですね。多くの仮定を経ている概念なので、解釈が難しいのです。
ベイズ確信区間 (Bayesian credible interval)##
もっと直感的に、興味あるパラメーターの範囲を計算して、「このパラメーターがこの範囲に含まれる確率は95%!」と言いたいですよね。ここで登場するのがベイズ確信区間 (Bayesian credible interval) という考え方です。
カギとなるのは、ベイジアン (Bayesian)の哲学です。頻度論者とは異なり、ベイジアンは「パラメーターは真の値を持つ」などとは考えません。その代わり、「パラメーター$\theta$ は様々な値を取り、どの値を取るかは確率分布$P(\theta)$ による」と考えます。データ$y$ を与えるモデルパラメーター$\theta$ を決めると、以下のベイズの定理が成り立ちます。
P(\theta|y) = \frac{P(y|\theta)P(\theta)}{\Sigma_{y}P(y|\theta)P(\theta)}
このとき、$P(\theta)$ は**事前確率分布 (prior distribution)**と呼ばれ、データを観測する以前における$\theta$ の値に対する確率分布を表します。
$P(y|\theta)$ は**尤度関数 (Likelihood)**と呼ばれ、モデルパラメーター$\theta$ が決まった時の、データ$y$ の確率分布を表します。
最後に、$P(\theta|y)$ は** 事後確率分布 (posterior distribution)**と呼ばれ、データ$y$ を観測した後における、モデルパラメーター$\theta$ の確率分布を表します。
このベイズ統計学の良いところは、興味のある値$\theta$ の取りうる範囲が(実験後の確率、つまり事後確率分布として)表現されているため、例えば、95%の**$\theta$が含まれる範囲をその事後確率分布$P(\theta|y)$ から直接計算できる**点です。
そのため、ベイジアンの哲学の下では、ベイズ確信区間を計算することにより、「興味あるパラメーターがこの範囲にいる確率は$p$である!」と直感的な結論が導けるのです。
(例題) 信頼区間 vs ベイズ確信区間##
理解を補強するために、簡単な例題を解いてみましょう。
A君には悩みがあった。自分はじゃんけんが弱いのではないかという悩みだ。そこでA君は、じゃんけんをするごとにその結果を記録することにした。あいこになったときは、勝つか負けるまでその相手とじゃんけんをした。100回じゃんけんをしたうち、A君が勝った回数は42回だった。このとき、A君はじゃんけんが弱いといえるか。
このA君のお悩みに、頻度論者 (Frequentist)、ベイジアン (Bayesian) それぞれの立場から答えてみましょう。
「頻度論者の解答」###
A君の勝率$\theta$ は記録からすると42/100だが、これは100回という限られた試行の中で得られた結果、母集団の一部しか観れていないことによる結果であり、**A君の勝率$\theta$ は、唯一無二の真の値が存在する。**真の値が何か?そんなことはわからん。だがしかし、A君がじゃんけんに弱いかどうかはわかる。信頼区間を計算すればいいのだ!
今回の母集団は、複数の独立した試行の元、勝つ確率$\theta$、負ける確率$1-\theta$ の2通りの結果だから、**二項分布 (Binomial distribution)**になる。このとき、100回のじゃんけん結果から得られた勝ち数の分布の平均は、**中心極限定理 (central limit theorem)**より、平均$100\theta$、分散$100\theta(1-\theta)$の正規分布に従うとしてよい!分散既知なので$z = 1.96$を用いて、95%信頼区間は以下のように計算できる。
(100\theta - 1.96\sqrt{100\theta(1-\theta)}, \hspace{5pt} 100\theta + 1.96\sqrt{100\theta(1-\theta)})
観測された勝率$\theta = 42/100$ を代入すると、信頼区間は$(32.3, 51.7)$と計算できる。つまり、100回じゃんけんをして勝率を求める実験をものすごーくたくさん繰り返せば、そのうち95%は$32.3 \leq 勝ち数 \leq 51.7$となるってことだ!この範囲には強くも弱くもない勝ち数50が含まれているから、私は95%の自信をもって、A君はじゃんけんが弱くないと言おう!
「ベイジアンの解答」###
今回のじゃんけんは、複数の独立した試行の元、勝つか負けるかの2通りの結果だから、データ$y$ を与える確率分布は**二項分布 (Binomial distribution)**になるよね。この確率分布のモデルパラメーター、今回の場合、勝率を$\theta$ とすれば、試行回数$N$、勝ち数$y$ として、この確率分布は以下のように書ける。
P(y|\theta) = \binom{N}{y}\theta^{y}(1-\theta)^{N-y}
モデルパラメーター$\theta$ が決まってるとすれば、上式をベイズの定理における尤度関数として扱っていいね。もちろん$\theta$ はこれから、事前確率の式$P(\theta)$ と掛け合わせて求めるわけだけど。
さて、モデルパラメーターの事前確率$P(\theta)$の確率分布だけど、ベータ分布としてみよう。今回は尤度関数$P(y|\theta)$ が二項分布なので、事前確率分布$P(\theta)$ がベータ分布なら、求めたい事後確率分布$P(\theta|y)$ もベータ分布になるから、計算が楽になる。このように、事前確率分布と事後確率分布が同様の確率分布になるような事前確率分布を共役事前確率分布 (Conjugate prior) と呼ぶけど、それはまぁいい。
ベータ分布には、事前確率分布のパラメーター (hyperparameter) が、$\alpha, \beta$ と2つある。
\theta \sim Beta(\alpha, \beta)
$\alpha, \beta$ は、ベータ分布の平均が$\frac{\alpha}{\alpha + \beta}$、サンプルサイズが$\alpha + \beta$、 ということを利用して決めよう。
今回のじゃんけんは、勝つか負けるかの2通りだから、事前確率分布$P(\theta)$ の平均が$0.5$ になるようにしたい。サンプルサイズは$100$ だから、$\alpha = \beta = 50$ でいいかな。
このとき、尤度関数$P(y|\theta)$ が二項分布なので、共役事前確率分布の性質により、事後確率分布$P(\theta|y)$ は以下のように書ける。
\theta|y \sim Beta(\alpha + y, \beta + N - y)
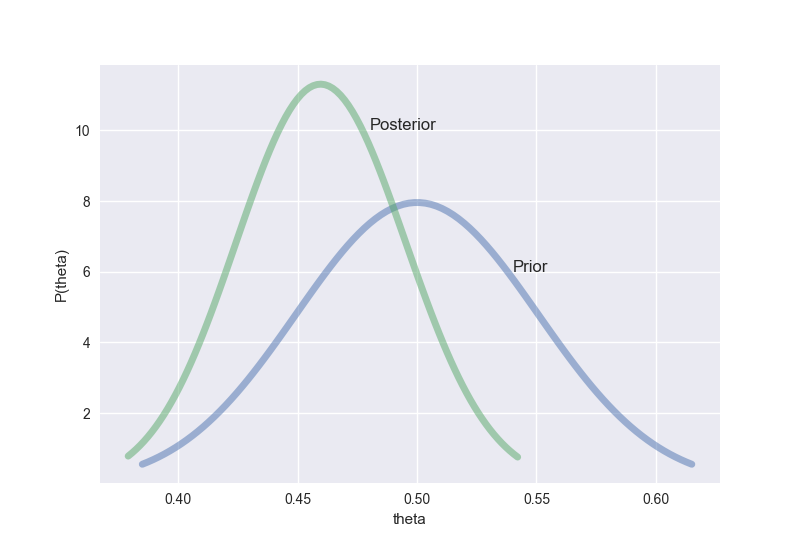
パラメーターの値を代入すると、事前確率分布は$Beta(50,50)$、事後確率分布$Beta(92,108)$となるね。それぞれの分布をグラフにするとこうなる。
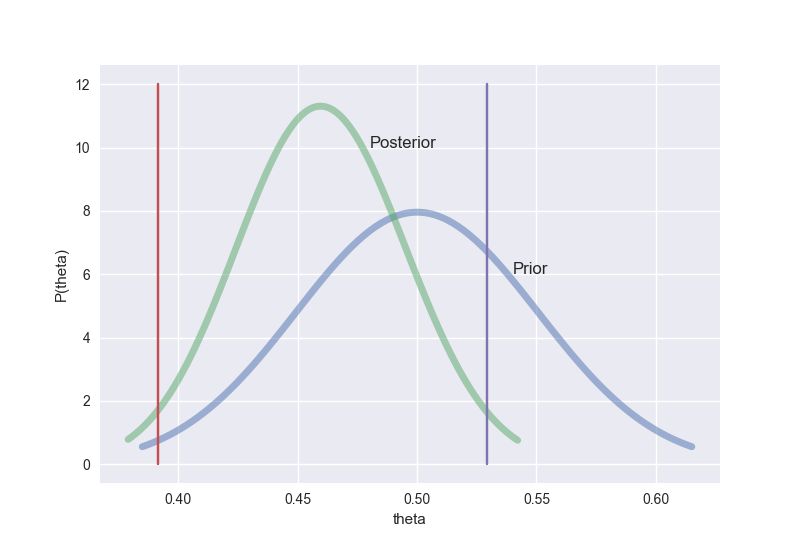
最後に、肝心の95%ベイズ確信区間を求めよう。要は、事後確率分布で95%のデータが含まれる範囲を計算するだけで、結果は$(0.392,0.530)$ となる。グラフだと、赤ラインが確信区間の下限、紫ラインが確信区間の上限を示している。
この結果から、A君の勝率は95%の確率で$(0.392,0.530)$の範囲にいることになる。まぁ、ちょっと弱い傾向はあるけど、五分五分の勝率である$\theta=0.5$ がこの範囲に含まれているし、A君はじゃんけんが弱くないと言っていいんじゃないかな。
まとめのまとめ##
- C%信頼区間は、実験をたくさん繰り返した (N回) とき、興味あるパラメーターがその区間内にいる実験の回数がだいたいNC回ある、という意味を持つ。
- ベイズ統計学では、確信区間といってパラメーターがある範囲に含まれる確率を直接計算できる。
おわりに
信頼区間は統計学で最初の方に習う基本概念ですが、実は解釈が難しいのですね。ベイズ統計学を用いるとより、人間の直感に沿った解釈が可能になりますが、計算過程がより煩雑になるきらいがあります。結局は哲学の違いなので、好みによって使い分ければいいと思います。
以下に、今回の例題を解いてグラフを描画するためのコードを載せておきます。
# library
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# A-kun data
p = 42/100
n = 100
# Frequentist -------------------------------
# due to the binomial distribution with the central limit theorem...
mu = 100*p
sigma = np.sqrt(100*p*(1-p))
ci = norm.interval(0.95, loc=mu, scale=sigma)
# Bayesian ----------------------------------
from scipy.stats import beta
# plot beta distribution
fig, ax = plt.subplots(1,1)
def plotBetaPDF(a,b,ax):
# range
x = np.linspace(beta.ppf(0.01, a, b), beta.ppf(0.99, a, b), 100)
# visualize
ax.plot(x, beta.pdf(x, a, b), lw=5, alpha=0.5)
ax.set_xlabel('theta')
ax.set_ylabel('P(theta)')
# prior beta distribution
a = 50
b = 50
plotBetaPDF(a,b,ax)
ax.text(0.54,6,'Prior')
# posterior beta distribution
a = 50+42
b = 50+100-42
plotBetaPDF(a,b,ax)
ax.text(0.48,10,'Posterior')
# plt.close('all')
# 95% Bayesian credible interval
bci = beta.interval(0.95,a,b)
print('95% Bayesian credible interval:' + str(bci))
ax.plot(np.array([bci[0],bci[0]]),np.array([0,12]))
ax.plot(np.array([bci[1],bci[1]]),np.array([0,12]))