まとめのまとめ
- 生物の進化のダイナミクスも、脳による記憶のメカニズムも、限られた容量内で将来の種の繁栄や意思決定を最適化するため、ベイジアンサンプリングの一種であるパーティクルフィルターを採用しているように思われる
- 創造性を科学するための理論 (BSVR; Blind Variation and Selective Retention theory) は、同じくベイジアンサンプリングの一種であるMCMC (Markov Chain Monte Carlo)を用いて、確率的探索アルゴリズムとして読み替えることができる
序章「ダーウィン」
「おかしいですわ……!」
マユコは自室で1人、肩を震わせた。
彼女は今年4月から〇〇工科大に進学予定の、女子高生という肩書きの有効期限が失効しかかっているお嬢様系女子高生である。エンジニアをしている兄に憧れ、出身の女子高では進学先としてまず候補にすら上がらない工科大学を志望し、同級生に「えっ、それどこー?」「高価大……たかいの……?」などと言われながらも見事合格。大学生活への期待と不安でいっぱいのマユコは、入学式より前に期待と不安でいっぱいいっぱいになり、今日は大学の下見に行ってきたのだった。
そんなマユコを待っていたのは、工科大学の厳しい現実だった。
「どうしてあそこまでイケメンが少ないの!?ってかいないの!?」
春休みなので学生はそれほどいなかったが、それでもキャンパス内のカフェテリアなどにはそれなりの数の学生がいた。しかし、マユコの必死なキャンパス内しらみつぶし探索 (Exhaustive search) にも関わらず、女子高で培ったたくましい妄想力をかきたてる素敵な殿方は見つからなかった。
「おかしいですわ……!」
マユコは本日何度目かわからないこの言葉を口にして、額に手をあて首をかしげた。
「わたくしが高校の生物で学んだ知識によりますと、生存に適さない形質は自然淘汰されていくはずなのですわ。X染色体を1つしか持たない劣った生き物が生存していくためには、X染色体を2つ持つ私たち女性に必死にアピールしなくてはいけないはず。そして、イケメンとは……!」
マユコは兄から譲り受けたPCのエディタを立ち上げ、抑えきれない気持ちをそこに書き殴った。
while(LIFE)
{
string* state = readState();
if (state == "見た目に恵まれている")
state = "気持ちに余裕がある";
if (state == "気持ちに余裕がある")
state = "他人に優しくできる";
if (state == "他人に優しくできる")
state = "内面が磨かれる";
if (state == "内面が磨かれる")
state = "内面の良さが外面にも現れる";
if (state == "内面の良さが外面にも現れる")
state = "見た目に恵まれている";
updateState(state);
}
「......このループを回し続けられる、すなわち男性のイデアなのですわ!なのに、なのに……!」
マユコは思わず目頭を押さえた。
「あんな"state = 小汚い"がまだあんなにたくさん存在していたなんて!わたくしはドラマや漫画をたしなんでいる間に、ああした存在はとうに"LIFE == False"になったのかと思ってましたのに!!」
マユコが絶望のあまりPCのキーボードに突っ伏したそのとき、家のチャイムがなった。午後7時。兄のシュウが仕事から帰ってきたのだ。
マユコはのそのそと立ち上がり、ドアを開けて兄を出迎えた。
「……お帰りなさい、お兄様」
「あ、うん、ただいま……って、マユコ、どうしたの?」
打ちひしがれたような妹の様子を見て、シュウは何かよくないことが起きたと悟った。心配するシュウを見上げ、マユコは力なく微笑んで言った。
「お兄様、ダーウィンは間違っていたのかもしれません」
第一章「進化論のアルゴリズム」
同日午後八時。
大学へ行ったこと、しらみつぶし探索でも解(=イケメン)が見つからなかったこと、現代にも非イケメンが多数生存していることにショックを受けたこと、これは進化論に反するんじゃないかということを、マユコはもりもり晩御飯を食べながらシュウに打ち明けた。シュウは、妹の底知れぬ食欲と話の内容に多少の戦慄を覚えながらも、後片付けが終わった後こう切り出した。
「じゃあ、進化論を簡単にシミュレーションしてみようか」
"イケメン 多い 大学"というキーワードをまさにGoogle先生に投げようとしていたマユコは、目を丸くしてシュウを見た。
「え……お兄様はそんなこともできるんですか」
シュウは少し自分の髪を触った。
「僕はっていうか、この世の多くの現象はアルゴリズムの形に蒸留することができるって話。進化論もその例外じゃないってこと。The price equationとか知らない?」
マユコは首を横に振った。
「わたくしお金にはまだ疎くて……それは女子高生と女子大生、どちらのプライスに価値があるかみたいな興味深いお話ですか」
「確かに興味深い……いや待ってそれ何の話。これ、ある形質の発生頻度を表現する数学の公式でね、簡単なやつだと……そうだ、例えばマユコは、イケメンの話してたじゃん」
マユコの目が輝いた。
「イケメン!」
「う、うん……。とりあえず世代$t$ におけるイケメンの存在確率を$P_{イケメン}^{(t)}$ とおくよ」
マユコは再びエディタを開き、メモを取り始める。その様子を見ながら、シュウは続けた。
「そして、世の中にはいろんな形質があるけど、それぞれのメリットというか、生き残りやすさの尺度をフィットネス$f$とするよ」
マユコは大きくうなずいた。
「なるほど、つまり$f_{イケメン} = 100$%というのが公式なのですね」
「それイケメン以外全滅してるよね。そしてそれが公式として数学界に残ってたらもう数学界終わりだわ。まぁとにかく、このとき世代$t+1$ におけるイケメンの存在確率は以下のように書ける」
P_{イケメン} ^{(t+1)} = \frac{f_{イケメン}P_{イケメン} ^{(t)}}{\sum_{j}f_{j}P_{j}^{(t)}}
マユコが硬直して動かなくなったので、シュウはあわてて補足をいれた。
「こ、この分母はちょっと難しく見えるけど、ただの全体の形質のフィットネスの平均、期待値だからね!……つまりこの式が意味するのは、今の世代におけるイケメンのフィットネスが、全体のフィットネスの平均より高ければ、次の世代はイケメンが増えますよ、ってこと」
マユコはエディタに書かれた式をじっと見つめ、考え込み、ややあって再びシュウに視線を戻した。そして言う。
「お兄様。わたくし、」
続けて、
「興奮してきました」
「え……」
虚をつかれたシュウをよそに、マユコは熱い口調で話し出した。
「この一見単純な式、すごいですわ。ダーウィンの言う環境収容力 (Carrying capacity)、すなわちこの世界が許容できる生物量に限界があるから、同一種内でも形質ごとにフィットネス、つまり生き残りやすさに差が生まれる……それは知っておりました。それがこんな簡単な式で、次世代の形質の存在確率をモデル化できるなんて……!」
目をキラキラさせていたマユコはふと我に返る。瞳に不気味な光が宿った。
「……ということは、現世代の非イケメンを全員惨殺すれば……!$f_{非イケメン }= 0$ になるので、次世代にイケメンパラダイスを実装できることになりますわ!!」
「なんで惨殺!?その無駄な残忍さは社会に出るまでに捨てておいてね……。まぁともかく、マユコが見たように現世代にもまだまだたくさんイケメンじゃない人たちがいるってことは、イケメンのフィットネスはそれほど高くないんじゃないかな」
そう言うシュウを、マユコはまじまじ見つめた。
「……お兄様がそう思いたいお気持ちはよくわかります。だってお兄様はー」
「それ言わなくていいやつ!折角このお話は文字ベースなんだから余計な情報!!」
「そうでしたわ。ごめんあそばせ。でも、」
マユコはシュウを見つめてにっこり笑った。
「現代はまだ自然淘汰の途中なのかもしれませんわ」
「くっ、た、確かにっ……」
さっきまで高説を垂れていたシュウは、ガックリ膝を落とした。マユコはにこにこしながら、エディタを閉じ、再びGoogle先生との哲学的門答へと戻ろうとした。より自然淘汰が進んでいそうな大学を探そうとする矢先、シュウはうなだれた首を持ち上げ、言い放った。
「マユコに宿題を出す」
「ひいぃぃっ!お兄様からの宿題っ……!!」
マユコは座ったままジャンプし、そのまま後ろ向きに壁まで後ずさった。マユコの脳裏には今まで兄から渡された宿題の数々が思い浮かんだ。最近だと大学合格が決まった後のこと。マユコが喜んでシュウに合格を報告すると、シュウも一緒になって喜んでくれた………そして翌日以降毎日、プログラミング未経験のマユコに容赦ないプログラミング課題を降り注いだのだった。その結果、マユコは一日に全くコードを書かない日があると、罪悪感で夜眠れなくなるという全国の女子高生を探しても極めて珍しい症状を抱えるまでに成長した。
「結局まだ進化論のシミュレーションやってないからね。Wright-Fisher model のシミュレーションをしてもらう」
そう言って、モデルの細かい説明を始めるシュウを、マユコはうなだれながら、ぼやけた瞳で見ていた。
あはは、これだからイケメンじゃないやつはー……
第二章「対立遺伝子とWright-Fisher model」
その週末、マユコはぼーっとエディタを見ていた。そこには先日宿題に出されたWright-Fisher Modelの宿題内容が書いてあった。
Wright-Fisher Model
- 進化論のモデルの1つで、対立遺伝子 (allele) の頻度を記述するために作られた
- ある集団に属する個体数をNとし、これは世代毎に変動しないとする
- 世代と世代はかぶらない (discrete, non-overlapping)
- 世代毎に全ての個体は新しい個体に入れ替わる
- 新世代の新しい個体が持つ対立遺伝子の割合は、1つ前の世代が持つ対立遺伝子の割合によってランダムに決まる
このとき、ある対立遺伝子A, aが0世代(ヒトの集団)に存在する確率$P(AA)^{(t=0)},P(Aa)^{(t=0)},P(aa)^{(t=0)}$ をそれぞれ適当に決め、シミュレーションによって少なくとも20世代までその対立遺伝子の存在確率がどう変遷していくか観測しなさい。世代の個体数Nも自分で決めてよい。
マユコは対立遺伝子 (allele) のことは高校で勉強したので知っていた。染色体には遺伝子座 (Locus) と呼ばれる遺伝子を格納する場所があり、人の場合2倍体といって、父親と母親から1つずつ、そこに入る遺伝子を合計2つ譲り受ける。そのとき、同じ遺伝子座の2つの遺伝子が互いに異なった情報を持っているとき、その遺伝子は対立遺伝子と呼ばれる。例えば、ある遺伝子座にはAかaの遺伝子が入れるとすると、Aとaは互いに対立遺伝子で、その組み合わせはAA, Aa, aaの3通りある。
「もしAが優性のイケメン遺伝子で、aが劣性の〇サイク遺伝子だったら、AA, Aaを持っている人はイケメンになるけれども、aaの人は〇サイクになってしまうのですわ……つまりお父様がイケメンでも、それがAa由来だった場合、ご子息がaaになってしまう可能性だってあるのですわ……!」
当時高校1年生のマユコは、運命の残酷さに身震いしたものだ。
そして現在ーーー
「やはりこれは………わけわかめなのですわ!!」
ばんっと机に両手を打ち、マユコは立ち上がった。そのままラップトップを抱えて自室を飛び出し、居間で雑誌(ニュータイプ)を読んでくつろいでいるシュウのところへダッシュ。
「ニートタイム終了のお知らせ!」
「はっ、ひいぃぃっ!」
マユコがシュウの読んでいた雑誌を華麗にダストシュートすることによって、シュウの束の間の休息はそこで終了した。マユコは突然目の前から雑誌が消えたショックで茫然としているシュウの前に仁王立ちし、高らかに言い放つ。
「さぁお兄様!ここまで辛抱強くこのお話を読んでくださったQiita読者の方々のために、わたくしの宿題を や さ し く 解説して差し上げて!!」
「え、えっ、えー……ちょ、それマユコの宿題……」
「そんなことは今は関係ないのっ!お兄様がぱっと解説してくださらないと紙面が足りなくなってしまいますわ!!ただでさえ本筋とは全く関係ない無駄ディテールに紙面を取られていますのよ!!!」
「え、あの、ほとんどのディテールはマユコのであって僕のじゃな……」
シュウの言葉は、マユコがラップトップを突き出すことによって遮られた。
「はい、いいからここに書くのです!ライトフィッシュモデルのシミュレーションを!!」
「あ、ライト・フィッシャーね……はい……」
勢いに押され、シュウはマユコのエディタにpythonで関数を1つ書いた。
def wright_fisher_simulation(repeat, N, pAA, paa):
'''simulation of Wright-Fisher model:
repeat: the number of repeat in simulation
N: the number of individuals in the population
pAA: the probability that an individual has AA
paa: the probability that an individual has aa
(hence the probability that an individual has Aa
is 1 - pAA - paa)
'''
# attribute allele to individuals as 1st generation
results = [[np.random.choice([0, 1, 2], N, replace=True, p=[paa, 1-pAA-paa, pAA])]]
# iterate Wright-Fisher process
for r in np.arange(repeat-1)+1:
pAA = np.sum(results[r-1][0]==2)/N
pAa = np.sum(results[r-1][0]==1)/N
paa = np.sum(results[r-1][0]==0)/N
results.append([np.random.choice([0, 1, 2], N, replace=True, p=[paa, pAa, pAA])])
return results
一息ついてシュウは言った。
「メインの関数は、こんな感じ。まず0世代目N人を、AAを持つ人、Aaを持つ人、aaを持つ人に分ける。それ以降の世代は、1つ前の世代のそれぞれの遺伝子の組み合わせの頻度の比を使って、N人分の遺伝子の組み合わせをランダムサンプリングすることを繰り返すだけ」
シュウが書いた関数をじーっと見つめ、マユコはつぶやいた。
「……じっそうは、いがいにかんたん、しんかろん」
「何で川柳?でもちろん現実の世界はもっと複雑なのは忘れないでね。世代は連続しているし、世代毎の人数Nも毎回バラバラになるし」
「さすがですお兄様」
「いやいや……でも折角だし自分たちで初期確率を決めて、実際にシミュレーションしてみようか!」
おだてられるとすぐ調子に乗るシュウは、アニメーションを作成する関数も書いた。
「とりあえず、$P(AA)^{(t=0)}=0.45,P(AA)^{(t=0)}=0.30, P(aa)^{(t=0)}=0.25$ として 走らせてみよう」
「では、AA>Aa>aaというフィットネスなのですね」
「そう考えてもらっていいよ。じゃあやってみよう!コードはこの記事の終わりに置いておくよ」
2人でこのアニメーションをしばらくじっと観た。途中からマユコは、
「ふ、ふふふ、うふふふふふ………」
と不気味な笑い声を出しはじめたので、シュウはぎょっとする。
「えっ、何、どうしたの……?」
若干の恐怖心に震えるシュウに、マユコは満面の笑顔を向けて言った。
「お兄様、第24世代くらいで、この世はイケメンパラダイスになるのですね」
第三章「ワーキングメモリー」
「わたくし、もう歳なのかしら」
「急にどうした」
マユコが〇〇工科大学にめでたく入学してから数日が経ったある日。2人でいつものように晩御飯を一緒に食べているとき、マユコがこぼした言葉にシュウは思わず妹の顔をまじまじと見つめた。
「マユコ、今何歳よ」
はぁーっとため息をついて、マユコは答える。
「18ですわ」
「喧嘩売ってんの?ねぇそうなの??」
思わず味噌汁の入ったお茶碗の手が震えるシュウを見て、マユコは慌てて説明をした。
「ち、違いますわもちろん。ただ、最近とてもたくさんのサークル勧誘のチラシをいただくのですが……」
ごはんの入ったお茶碗を置いて、まゆこは自分のカバンからどっさり束になったチラシを取り出した。
「……正直、色々比べているうちに自分が何をしたいのかよくわからなくなってきますの。最初の方に見たものをどんどん忘れていくのです」
あれ、自分が新入生のときそんなにチラシもらったっけ……同じ大学なんだけど……?そうした疑問が泡のようにふわっとシュウの脳に浮かんできたが、自分と妹のなんらかの絶望的な差が明らかになる気がしたので深入りはしないことにした。
そんな兄の様子に気付かず、マユコは尋ねる。
「お兄様は以前、世の中の多くの現象はアルゴリズムの形で蒸留できる、とおっしゃっていましたね。このわたくしを悩ませる問題も、アルゴリズムになるのでしょうか」
考えるトピックが自分の得意なフィールドになり、シュウはほっとする。
「あぁ、それはワーキングメモリー (Working memory) じゃない?歳っていうより」
「わーきんぐ・めもりー?確かにお兄様のお好きそうなアニメのタイトルですけど……」
「いや違うよ。うん、なんかそういうアニメありそうだけど、そうじゃなくて、いわゆる記憶を一時的に貯める脳の保管庫のことね」
「あぁ、マジカルナンバー (Magical number) とかのお話ですね。人間が瞬間的に覚えられる情報の最大数は7±2であるとかいう。だから郵便番号は7桁になっているとか」
「なんで詳細は知っているの?……まぁいいや。記憶実験では、被験者にまず色んなアイテムを、例えば6個、覚えてもらう」
マユコは少し考えて、
「キズぐすり、まひなおし、どくけし、ねむけざまし、げんきのかけら……」
「いや、それ本当にアイテムだね。特定のゲームに出てくるやつだよね。実際はもっと、互いに関連性が薄いものが選ばれる。ベッド、りんご、とか」
「ポケコインとか」
「それコインでいいよね?まぁそれで、被験者は最初は6個全部覚えているんだけど、時間が経つにつれてどんどん忘れていく。この、時間を横軸、覚えているアイテム数を縦軸にグラフにすると、有名な忘却曲線 (Forgetting function) が得られる」
「エビングハウスですね」
「そう、こんなやつ」
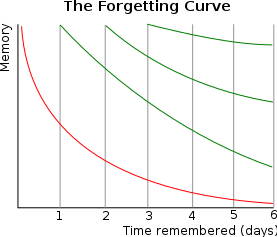
(https://en.wikipedia.org/wiki/Forgetting_curve)
マユコは少しうつむいてじっと考えた。ややあって、シュウを見つめて問う。
「でもそれって、それぞれのアイテムが自分にとって等しく興味がないときのお話ですよね?例えば、この記事を読んでくださったQiita読者さまは、20分後にはお兄様のお名前を忘れているかもしれませんが、わたくしが マ ユ コ という美しい名であることは一生忘れることはないでしょう」
「その自信はどこから来るんだ。新歓か?新歓なのか??そしてさりげなく自分の名前強調したよね」
「このような、客観的なアイテムと、それに対する主観的な価値……それらを結ぶアルゴリズムなんてあるのでしょうか」
「スルーした!?……あぁ、うん、こういう記憶とか、脳の高次機能はパーティクルフィルター (Particle filter) を使うとモデリングできることがわかっている」
マユコはけげんな顔をした。
「ぱーてぃくる・ふぃるたー?またアニメですか??」
「違うし!パーティクルフィルターは逐次モンテカルロ法 (Sequential Monte Carlo: SMC)とも呼ばれるサンプリング手法で、事後確率分布 (Posterior probability distribution) を近似するために使う………そうだ」
いいことを考えた、とシュウは言って、マユコを見る。そして微笑んだ。
マユコの背中に冷や汗が流れた。
「……ま、まさかお兄様」
シュウはにっこり笑って言った。
「宿題だ」
「ひっ、ひいいぃいぃぃ!お、お兄様!!わ、わ、わたくし今サークルを選んだりサークルを選んだり、それにそれに、サークルを選んだりするのに忙しくて……!」
青ざめて慌てふためく妹を見て知らずか、シュウは言い捨てる。
「適当な記憶実験のデータを渡すから、それをパーティクルフィルターでフィットしてもらおうかな。期限は3日ね」
ごちそうさま!と言って、シュウは食卓から自分の食器を引き上げた。
1人残されたマユコは茫然としながら、それでも夕食を食べ終わる前に1つの決断を下した。
わたくし、ぜーったいにイケメンの方がいらっしゃるサークルに行きますわ……
第四章「パーティクルフィルター」
翌日夜、シュウが仕事から疲れて帰宅するなり、マユコが出てきてラップトップの画面を突き出してきた。
「できました」
「え……何が……ごはん……?」
「寝言はお休み中におっしゃってください。食事を作るのはお兄様のお務めなのですわ。もちろんパーティクルフィルターによるフィッティングです」
シュウはじーっと画面を見つめた。そしてため息をつく。
マユコの顔に若干の不安の色が浮かんだ。
「……間違ってますか?」
「いや、できてるね」
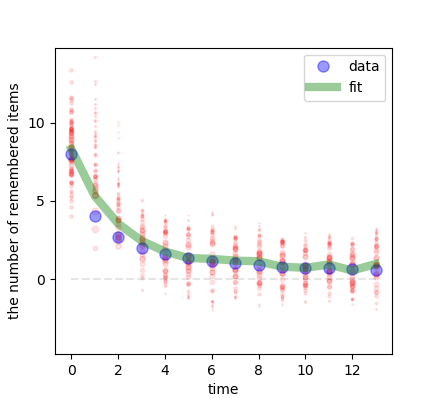
シュウには驚きだが、シュウが与えたデータに沿って、綺麗にラインがフィットされている。ご丁寧にも、尤度を表すパーティクルまでプロットされている。
よしっ!とマユコは両腕でガッツポーズした。居場所がなくなり落下しかけたラップトップを、シュウが慌てて支える。
2人して家の中に入って、食卓に向かい合って座る。水を一杯飲んで、シュウは一息ついた。そしてマユコに言う。
「正直驚いた。こんな短期間でできるとは思わなかったよ」
マユコはにこにこしながら、少し照れたように首を傾けた。
「ありがとうございます。……でも実は、こちらのパーティクルフィルターに関する記事をかなり参考にさせていただきました。おかげさまでマイナーチェンジで実装ができましたわ」
あぁなるほど、とシュウは相槌を打った。別に構わない。既存で良いものがあれば、それを使えばいい。理解した上で使えているなら、それで良いだろう。
「ところで」
シュウはマユコと向き合って、尋ねた。
「何か気づいた?」
マユコの頭の上でクエスチョンマークが躍った。
「なにか……ですか?」
シュウはうなずく。
「そう、この前はWright-Fisher modelという進化論のモデルシミュレーションの宿題を出した。今回はParticle Filterに関する宿題だ。その2つを連続して出したのは意味があってのことだったんだけど」
少し考えて、それでも考えながら、マユコは話す。
「意味……ですか。……そういえば、何と言いますか、Wright-Fisherは進化論、Particle Filterは記憶をモデリングするために用いましたが、どちらも、時間$t$ の状態が時間$t+1$ の状態に影響していました」
マユコの答えに、シュウは満足気に大きくうなずいた。
「そうなんだよ、よく気がついた!実は、Wright-Fisher modelとParticle filterは、基本的には同じものなんだ」
マユコの目が点になった。しばらく硬直し、立ち上がって、その場でくるんと一回転し、また着席した。そして、
「えぇーーーー!!!」
「ちょっ、マユコ声大きい!てか何その一連のモーション、理解できないんだけど」
「わたくしも理解できません!進化論のモデルと記憶のモデルが同じだなんて!!」
マユコが前のめりになり、シュウは思わず身体を引いた。目と目が合って、一瞬の沈黙。困ったように微笑んで、シュウが口を開いた。
「いや、でも基本的にはマユコの言った通りなんだ。Particle filterは、事前確率分布 (Prior probability distribution) からパーティクル……仮説の数だけサンプリングすることで始まるよね。そしていざ、データを観測したとき、それぞれのパーティクルは、それが表す仮説を元に、与えられたデータが観測される確率、つまり尤度 ($P(data|hypothesis): Likelihood)$ によって重みづけられる。各重みは標準化された後、次の時間$t+1$ でのパーティクルのサンプリングに用いられる」
「そうです。パーティクルフィルターは各時間毎に、もともと持っていた仮説と観測されたデータの情報を組み合わせて、新しい仮説を作ることができるのですよね。こうした情報を更新していく性質から、記憶のような脳の高次機能のモデルとして使える」
シュウは大きくうなずく。
「まさにその通り。そしてそれって、Wright-Fisher modelも一緒なんだ。各形質におけるフィットネスっていうのは、Particle filterで言うパーティクル、仮説だ。世代を経るごとに、各形質のフィットネスは更新されていく。実際に、どれだけその形質を持つ個体が生き残ったかというデータによって」
マユコはシュウの目をじっと見つめたまま、動かない。シュウからすれば、マユコがシュウの話を理解しているのかそうでないのかは、わからない。それでも、マユコがシュウの話している内容をしっかり考えていることはわかった。マユコが動かないのは、なるべく多くのリソースを、身体ではなく脳に割いているためだ。
「そしてね、」
シュウは続ける。
「進化論と記憶……この一見全く違う分野の意外に見える共通点は、実は意外でも何でもない。どちらもアルゴリズムとしては、**ベイジアン (Bayesian)**だから。マユコはベイズ統計学の基本はわかるんだっけ?」
こくっとマユコはうなずいて言う。
「手前味噌で恐縮ですが、ベイズ統計学って何だっけという方はこちらの記事がおすすめです」
「ホントに手前味噌だな!だがよくやった!!……まぁとにかく、パーティクルフィルターがベイジアンなのは、ベイジアンサンプリングのアルゴリズムだから疑いようがないよね。進化論についてだけど、最初にマユコに紹介した超簡単バージョンの進化論モデルってあるじゃん?」
シュウは自分のラップトップを開き、式を書き込んでマユコに見せた。
P_{i} ^{(t+1)} = \frac{f_{i}P_{i} ^{(t)}}{\sum_{j}f_{j}P_{j}^{(t)}}
「はい、$i$=イケメンでしたね」
「う、うん……今は一般的に、$i$ はなんらかの形質を表すとするよ。ここでフィットネス$f = P(d|h_i)$ と置く。形質$i$ がどれくらい生き残るかって仮説があって、実際に形質$i$ を持つ個体どれくらい生き残ったか (d:データ)、つまり尤度だね。すると、この式って以下のように書き換えられるんだよね」
P(h_i|d) = \frac{P(d|h_i)P(h_i)}{\sum_{j}P(d|h_j)P(h_j)}
マユコはじっと式を見つめた。しばらくして、マユコはあっ...と息をのんだ。
シュウはにっこり妹に笑いかけた。
「そう、これベイズの定理だよね」
終章I「創造性の理論とMCMC」
「ふぅ……」
自室のベットに横になって、天井を見上げ、シュウはため息をついた。
目を閉じた。妹と交わした会話が蘇ってくる。進化論、記憶、そのどちらも支えるパーティクルフィルターというアルゴリズム……。
マユコはたいしたものだ、とシュウは昔から思っていた。
自分と違って、世の中の色々なことに興味がある。人と会って、話すのが好きで、自分からだけじゃなく、色々な人から知識を仕入れてくる。自分の意見を言うこともいとわない。まぁ、器量の良い男性に過度なバイアスがかかる傾向はあるが……
「あいつは成功しそうだな……」
シュウ自身は、他人から言われたことをこなすことは比較的得意だ。長男だからかもしれない。だが、研究でもアートでも企業でも、成功しているのは創造性のある人間だ。シュウのような、いい意味の優等生タイプは、結局誰をフォローするか……研究室の教授だったり、会社の上司だったり……で人生が決まってしまう。
上手くいけば周りに感謝するが、失敗すれば周りのせいにする。
どんな環境でもベストは尽くすが、環境を変える努力はしない。
創造性のある人間は、強い。自らの意思で環境を変えられると思っているし、そういう解決策を思いつく。
シュウがそんな当たり前のことを理解しはじめたのは、くしくも就職してからだった。何かとても悔しくなってシュウが調べたところによると、創造性、というのはとても曖昧な単語だが、一応それについての理論が存在するようだった。BSVR (The Blind Variation and Selective Retention Theory) と呼ばれ、名前の通り、
「創造性 (Creativity)とは、ランダムなアイデアを複数思いつき (blind variation)、その中から状況に対する利用価値によって選択する (selective retention) 能力のこと」
というように創造性を二段階のプロセスとして定義する理論だった。
「これもベイジアンだな」
そうシュウは思った。ランダムなアイデアは、互いに生き残りをかけて人間の脳の中で争い合う。そして、その利用価値、尤度と言い換えてもいい、が高いと判断されたものだけが採用される。まさに、進化論や記憶と同等のアルゴリズムだ。
ただ、創造性のモデルは、進化論や記憶のようにパーティクルフィルターというよりは、同じベイジアンでもMCMC (Markov Chain Monte Carlo) の方が適しているらしい。
人間の脳内に、ブレインストーミングのようなネットワーク (Semantic network) があるとすると、作曲する、といった創造的課題に取り組んでいるときに、その人がネットワークのどのノードからスタートして、目の前の課題に対する利用価値が高そうな別のノードにどう移行し、あるいは現在のノードに留まったりするのか……という過程を、確率的探索としてモデル化できるからだ。
だから、色々なことを経験し、知っている人間は創造的なのだ。単純に、Semantic networkが広大だから。同じキーワードから探索をスタートしても、他の人が持っていないようなノードを持っているので、他の人が絶対にたどり着けないような解にたどり着く。
ただ、これも良し悪しで、探索アルゴリズムはMCMC、つまり人によってさほど効率が変わらないと思われる。そのため、創造的でない人間や何も知らない人間の方が、問題によっては通過するノードが少ない分、早く解にたどり着くこともある……。
「ま、結局……色んな人がいていいってことなのかな……」
訓練された社会人であるシュウは、翌日のハードワークに備えるべく安らかな眠りに落ちた。
終章II「社会はどうやって知識を継承しているか」
"The estimation problem faced by a memory maintenance system is that of representing the environment in a way that is useful for the planning and execution of future action." (Suchow et al., Trends in Cognitive Sciences, 2017)
「……記憶維持システムが直面する推定問題とは、将来とるべき行動の計画と実行に利用できるような形で、外の環境を表象することである……」
マユコはふむむと腕を組み、大学のPCルームのふかふかの椅子に深く座り込んだ。マユコが考えていたのは、大学で受講しているロボティクス入門の授業で、先生がさらっと言った一節だった。人間もそうだが、ロボットにも無尽蔵のメモリはない。だから、ロボットに何かさせたいなら、人間と同じで、外の世界の情報を効率的に処理するシステムを組まなければならない………
「これは進化論にも当てはまるのですわ」
マユコは、先日兄と交わした一連の会話を思い出していた。
「ダーウィンは、環境収容力は常に生物の繁殖力より小さい、と言いました。この世が広大で、資源にあふれ、全ての生きとし生けるものの楽園ならば……無数の形質の個体が互いに争うことなく共存しているでしょう。けれど、地球は狭く、資源は有限……だから、自分たちの生物種を長く繁栄させたいと思ったら、争いに勝てるような、あるいは争いを避けられるような、環境に適合した個体の形質しか生き残れないようにするしかない」
マユコはふうっと息をついて、目をつむった。川登りの途中で力尽きた鮭の様子が、瞼の裏に浮かんだ。
「同様に、私たちの脳にもメモリの限界がある……周りの全ての情報を処理し、蓄えておくことはできない。だから、自分たちにとって優先度の高いもの、すなわち将来の意思決定にとって大切そうなものだけ、記憶しておく……」
鮭のイメージが消え、マユコが愛してやまないアイドルグループのイメージに移り変わった。マユコの推しメン以外のメンバーは、ぼんやりとした輪郭でそこに立っていた。
結局、生物の進化も、記憶も、システムとしては同様の問題を扱っているのだ。
そしてその問題に対する1つの解答が、ベイジアンサンプリングの一種である、パーティクルフィルター。
「……この社会も、色んなものが生まれ、そして消えていく……この日本にとって、そしてわたくしたちにとって意味のあるものは、重み付けされ、次世代に継承される確率が上がる……そうでないものは、長い目で見れば必ず淘汰される……」
マユコは瞼を開き、PCをシャットダウンして立ち上がる。次の講義、教養科目の認知心理学は隣の棟で行われる。時間に余裕を持って、PCルームを後にした。マユコの大学は工科大で、「教養科目とか役に立たないし時間の無駄だわー、マジだるくね」と言ってはばからない非イケメンは多く、クラスの飲み会の場でそうやってマユコに話しかけてきた者もいた。マユコはにっこり笑って、
「あなたのような人に比べれば大抵のものは役に立つでしょうし、わたくしたちがそれを気に入って、学び、覚えている限り、次の世代にも残っていくのですわ」
と返し、場を戦慄させた。
軽やかな足取りで、マユコは次の講義に向かう。先週同様、彼女は前の方の席を取ろうと心に決めていた。
(終わり)
突然イースター休みが降ってきたので、のび太と学ぶ「機械学習」~FX予測プログラムを作成~【第1話】if文作戦にインスパイアされたのもあり、この形式にしました。
引用・参考
Suchow, J. W., Bourgin, D. D., & Griffiths, T. L. (2017). Evolution in Mind: Evolutionary Dynamics, Cognitive Processes, and Bayesian Inference. Trends in Cognitive Sciences, 21(7), 522–530. https://doi.org/10.1016/j.tics.2017.04.005
コード
Wright-Fisher Modelのシミュレーション
# -*- coding: utf-8 -*-
"""
Create animation of Wright-Fisher model simulation, which looks similar to
the figure 1c in Suchow et al., 2017, Trends in Cognitive Science
Implementation of "Wright-Fisher model"
"""
# libraries ------------------------------
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# %%
# functions -----------------------------
def wright_fisher_simulation(repeat, N, pAA, paa):
'''simulation of Wright-Fisher model:
repeat: the number of repeat in simulation
N: the number of individuals in the population
pAA: the probability that an individual has AA
paa: the probability that an individual has aa
(hence the probability that an individual has Aa
is 1 - pAA - paa)
'''
# attribute allele to individuals as 1st generation
results = [[np.random.choice([0, 1, 2], N, replace=True, p=[paa, 1-pAA-paa, pAA])]]
# iterate Wright-Fisher process
for r in np.arange(repeat-1)+1:
pAA = np.sum(results[r-1][0]==2)/N
pAa = np.sum(results[r-1][0]==1)/N
paa = np.sum(results[r-1][0]==0)/N
results.append([np.random.choice([0, 1, 2], N, replace=True, p=[paa, pAa, pAA])])
return results
def allele_color(x):
'''color code for pairs of allele'''
if x==2:
col = "r"
elif x==1:
col = "g"
elif x==0:
col = "b"
return col
def animate(i):
'''for animation'''
plt.cla()
plt.axis('off')
plt.text(2.3, 6.7, "P(AA), P(Aa), P(aa)=" + str(pAA) + ", " + str(round(100*(1-pAA-paa))/100) +
", " + str(paa), fontsize=12, color="k", ha="left")
plt.text(-0.5, 6.7, "AA", fontsize=20, color="r", ha="left")
plt.text(0.3, 6.7, "Aa", fontsize=20, color="g", ha="left")
plt.text(1.1, 6.7, "aa", fontsize=20, color="b", ha="left")
plt.text(1.7, -0.9, "generation " + str(i), fontsize=20, color="k", ha="left")
if i <= ngene:
im = plt.scatter(generation[i][0], generation[i][1], marker='o', s=300,
c=generation[i][2], edgecolors='none')
else:
im = plt.scatter(generation[ngene][0], generation[ngene][1], marker='o', s=300,
c=generation[ngene][2], edgecolors='none')
return im
# %%
# visualize simulation steps
ngene = 100
N = 49
pAA = 0.45
paa = 0.25
results = wright_fisher_simulation(ngene, N, pAA, paa)
plt.close('all')
fig = plt.figure()
ims = []
ncol = np.floor(np.sqrt(N))
if ncol**2 < N:
nrow = ncol + 1
else:
nrow = ncol
generation = []
for g in range(ngene):
plt.cla()
x = [0]
y = [0]
c = []
for n in np.arange(N):
c.append(allele_color(results[g][0][n]))
if x[-1]+1 >= ncol:
x.append(0)
y.append(y[-1]+1)
else:
x.append(x[-1]+1)
y.append(y[-1])
generation.append((x[:-1], y[:-1], c))
# animation
ani = animation.FuncAnimation(fig, animate, interval=500)
ani.save('wright_fisher_animation.mp4',writer='ffmpeg')
Particle filterによる忘却曲線のフィッティング
Pythonによるパーティクルフィルタの実装と状態空間モデルへの適用を大変参考にさせていただきました。
# -*- coding: utf-8 -*-
"""
Create a figure, which looks similar to the figure 2
in Suchow et al., 2017, Trends in Cognitive Science
Implementation of "Particle filter" along with the following:
https://qiita.com/kenmatsu4/items/c5232b1499dfd00e877d
"""
# libraries ------------------------------
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# artificial data for a working memory task (n_object = 6)
lam = 8
t = np.arange(1,15)
n_remembered = lam/t + 0.05*np.random.rand(len(t))
# %%
# functions -----------------------------
class ParticleFilter(object):
def __init__(self, y, n_particle, sigma_2):
self.y = y
self.n_particle = n_particle
self.sigma_2 = sigma_2
self.log_likelihood = -np.inf
def norm_likelihood(self, y, x, s2):
return (np.sqrt(2*np.pi*s2))**(-1) * np.exp(-(y-x)**2/(2*s2))
def F_inv(self, w_cumsum, idx, u):
if np.any(w_cumsum < u) == False:
return 0
k = np.max(idx[w_cumsum < u])
return k+1
def resampling(self, weights):
idx = np.asanyarray(range(self.n_particle))
u0 = np.random.uniform(0, 1/self.n_particle)
u = [1/self.n_particle*i + u0 for i in range(self.n_particle)]
w_cumsum = np.cumsum(weights)
k = np.asanyarray([self.F_inv(w_cumsum, idx, val) for val in u])
return k
def simulate(self, seed=1220):
np.random.seed(seed)
# the number of data points in the time-series
T = len(self.y)
# x as a hidden state variable
x = np.zeros((T+1, self.n_particle))
x_resampled = np.zeros((T+1, self.n_particle))
# initialization of x as the number of items to be remembered
# initial_x = np.random.normal(0, 1, size=self.n_particle)
initial_x = self.y[0] + np.random.normal(0, self.sigma_2, size=self.n_particle)
x_resampled[0] = initial_x
x[0] = initial_x
# weight
w = np.zeros((T, self.n_particle))
w_normed = np.zeros((T, self.n_particle))
l = np.zeros(T) # initialization of likelihood in each time point
for t in range(T):
print("\r calculating... t={}".format(t), end="")
for i in range(self.n_particle):
# v as a system noise
v = np.random.normal(0, self.sigma_2)
x[t+1, i] = x_resampled[t, i] + v # add the system noise
# weights as particles' individual likelihood
w[t, i] = self.norm_likelihood(self.y[t], x[t+1, i], self.sigma_2)
w_normed[t] = w[t]/np.sum(w[t]) # normalization
l[t] = np.log(np.sum(w[t])) # log likelihood
# indices to be resampled
k = self.resampling(w_normed[t])
x_resampled[t+1] = x[t+1, k]
# overall log likelihood
self.log_likelihood = np.sum(l) - T*np.log(self.n_particle)
self.x = x
self.x_resampled = x_resampled
self.w = w
self.w_normed = w_normed
self.l = l
def get_filtered_value(self):
"""
filtered values based on weights
"""
return np.diag(np.dot(self.w_normed, self.x[1:].T))
def draw_graph(self):
T = len(self.y)
plt.figure(figsize=(6,6))
plt.plot(range(T), self.y, "ob", markersize=8, alpha=0.4)
plt.plot(self.get_filtered_value(), "g", linewidth=6, alpha=0.4)
plt.legend(['data', 'fit'])
plt.scatter(np.ones(self.n_particle)*0, self.x[0], color="r",
s=6, alpha=0.1)
for t in range(len(self.w_normed)):
# reflect the relative likelihood to the particle's marker size
zscore = (self.w_normed[t] - np.mean(self.w_normed[t]))/np.std(self.w_normed[t])
for e in range(self.n_particle):
plt.scatter(t, self.x[t+1][e], color="r",
s=6*(1 + zscore[e]), alpha=0.1)
plt.plot(range(T), np.zeros(T), '--k', alpha=0.1)
# %%
# preset hyperparameters
n_particle = 48
sigma_2 = 2
# apply a particle filter and visualize its result
pf = ParticleFilter(n_remembered, n_particle, sigma_2)
pf.simulate()
plt.close('all')
pf.draw_graph()
plt.xlabel('time')
plt.ylabel('the number of remembered items')
plt.ylim(-4.8,14.8)
plt.yticks([0,5,10])
plt.show()