脳がベイジアンだと思われる件
私たちは、不確実な世界に生きています。ゴミをゴミ箱に投げてもなかなか入りません(私は)。これは、私の脳が、私とゴミ箱の物理的な距離と、ゴミの重さといった物理量、また私自身の運動機能といった、サクセスフルにゴミを投げ入れるために必要な計算事柄を、正しく計算できていないことを表しています。
**認知科学 (Cognitive Science)**の世界では、**ベイズ統計学 (Bayesian Statistics)**を用いて、人や動物の認知・行動をモデリングする試みがなされてきました。ベイズの利点はもちろん、行動の達成に必要な計算事項に関する不確実性 (Uncertainty)を、確率を用いて定量できることです。人や動物は、不確実な世界から情報を取得し、記憶や経験と組み合わせて行動を実行します。そのためベイズ統計学を使って主観的な不確実性を定量することは、行動の理解に大きく貢献するわけです。
実際、このような確率モデル (Probabilistic model)は、視覚、運動、言語などなど複雑な認知・行動機能をうまく説明できます。今流行りの機械学習 (Machine Learning)のように、大量の教師データが必要ということもありません。これら、ベイズ確率モデルの成功例は、
「私たちの脳はベイジアン!世の中の不確実性は、確率で表現されている!!」
という説を一般的なものにしてきました。
それにしては私たちの確率計算があまりにもしょぼ過ぎる件
脳がベイジアンであれば、私たちは世の中のあらゆる現象を確率分布として脳内で表現し、最も合理的な行動をとることができるはずです。ところが、私たち人間はとてもそういうことができているようには思えません。以下のような例って、結構見られるんじゃないでしょうか。
「飛行機事故が怖くて飛行機に乗れない人」
「買わなければ当たらない!と宝くじを買いまくる人」
これらはBase-rate fallacyあるいはBase-rate neglectと呼ばれる現象で、実際に起こる確率を必要以上に高く見積もってしまう傾向のことを指します。また、以下も有名ないい例です。あるアメリカ人女性について説明がまずされます。
「リンダは31歳、独身、素直な性格で聡明。大学の専攻は哲学。学生時代には、差別・社会正義といった問題に深い関心を抱き、反核デモにも参加」
さて、リンダは次のどちらの可能性が高いでしょうか?
1.リンダは銀行窓口係である。
2.リンダは銀行窓口係で、フェミニスト運動に参加している。
.....................................
どちらだと思いますか?
Qiitaを見ているような人は、ちゃんと1を選べた人が多いかもしれません。銀行窓口係である確率は、銀行窓口係かつフェミニスト運動に参加している確率よりも必ず大きくなるからです。
P(銀行窓口係) \geq P(銀行窓口係)P(フェミニスト運動に参加)
そりゃそうですよね。ところが実際には、大多数の人が2を選んでしまいます。このように、より詳細な情報を与えられた出来事が起こる確率を実際以上に高く見積もってしまう傾向を、Conjunction Fallacyと呼びます。
これらの簡単な事例は、「脳はベイジアンで確率を表象している」という立場をぐらつかせます。
脳はベイジアンだが確率を計算していない件
これが今の流行りです笑 「どういうことやねん怒」と思われる人も多いと思いますが、つまりは以下のようにまとめられます。
「脳は確率を表象してそれをもとに計算しているわけではなく、ベイズ的サンプリングを行っている」
脳がナイーブにベイジアンを実装しているとすると、脳は全ての起こりうる事象について確率分布を計算していなければなりません。例えば、ドラえもんのアニメ(30分)1回で、以下のような日本語は平均して何回出てくるでしょうか?ただし、〇にはひらがな・カタカナが入ります。〇同士は違っていてもOKです。
〇〇〇〇ん
...........................
何回くらいですかね?
「ドラえもん」、「のびたくん」、「ジャイアン」など様々なパターンがありますね。
この問題をベイズ的に解こうとすると、以下の3ステップが必要になります。
- 知っている日本語全ての事後確率分布 (Posterior probability)を計算する
- それら全ての日本語から、ひらがな・カタカナ換算で5文字かつ最後が「ん」であるものをフィルタリングする
- それらフィルタリングされた日本語の事後確率分布を、アニメ「ドラえもん」からランダムサンプリングで得られた日本語の確率分布を元に更新する
ちょっと考えただけでも、恐ろしい計算量になりますね。脳は身体全体の2%程度の質量ながら、全体のエネルギーの20%ほどを消費する臓器です。そのため、脳がこうしたヘビーな記憶・計算をしているとは、生物学的に少し考えにくいです。
じゃあ脳はどうしているのか?
その答えが**ベイジアンサンプリング (Bayesian Sampling)**です。起こりうる事象に関する確率の多次元空間を、一歩づつ探索していき、より高い山(起こりやすい事象)を見つけていくプロセスです。記憶・計算の負荷は少ないですが、継続することで起こりうる事象の確率分布の全体像をつかむことができます。イメージで言うとこんな感じです。
 ([けものフレンズ4話](http://kemono-friends.jp/archives/story/04/))
([けものフレンズ4話](http://kemono-friends.jp/archives/story/04/))
かばんやサーバルはもともとこの世界の一部しか知りません。それでも、少しづつ探索をしていくことにより、全体像をつかんでいきます。
ベイズ統計学で言えば、**MCMC法 (Markov Chain Monte Carlo)**が最も有名なサンプリング法でしょうか。その中で最も簡単な、**メトロポリス・ハスティング法(Metropolis-Hastings algorithm)**を用いて、いかにシンプルなアルゴリズムが事後確率分布を近似できるか、示してみたいと思います。
メトロポリス・ハスティング法(MCMCの1つ)
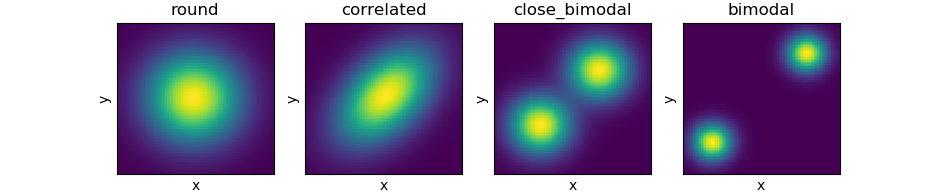
まず、事後確率分布として4種類の2変量正規分布 (Bivariate Gaussian)を準備します。
メトロポリス・ハスティング法では、現在の場所に基づいて次に移行するかもしれない場所をまず提案します。実際に移行するかどうかは、現在の場所の確率と提案された場所の確率を比較して決定します。このステップを繰り返すことで、事後確率分布に近いサンプリング分布を作ることができます。
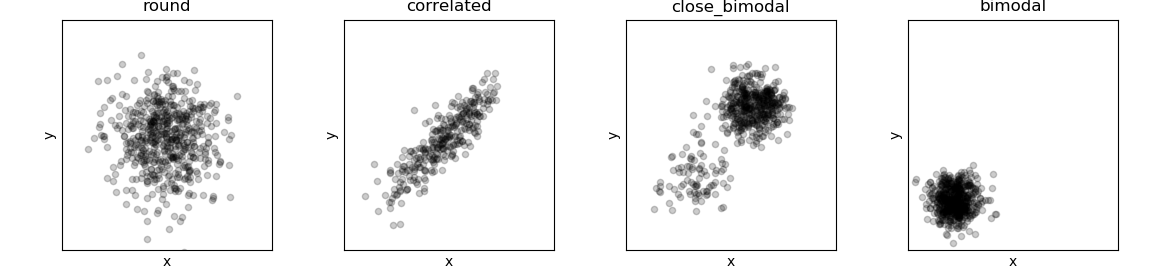
最初の2つ、roundとcorrelatedはメトロポリス・ハスティング法により、そこそこ綺麗に事後確率分布を近似できていますね。3つ目、close_distributionでは、明らかに近似が不完全です。2つある「山」のうち、1つの「山」については不完全な情報しか取れていません。最後のbimodalに関しては、事後確率分布では2つある「山」のうちの、1つを完全に無視してしまっています。
これらは、ベイジアンサンプリング特有の限界を如実に示した例です。どんな確率分布であれ、原理的にはベイジアンサンプリングにより近似することができます。が、サンプリング回数が有限であれば、その結果はどうしてもサンプリング開始点に影響されます。開始点の近くに高い確率を示す「山」が見つかればいいですが、そうでなければ迷子のままです。それっぽい「山」が見つかっても、それは最大値ではなく**極大値 (Local Maximum)**かもしれません。そして、「今の状態に基づいて、次の状態を決定する」というベイジアンサンプリングの特徴上、サンプリングされた状態は完全なランダムではなく、**自己相関 (Autocorrelation)**しています。
こうしたベイジアンサンプリングに伴って観測される特徴は、まさに我々人間の行動にも見られます。最初の方に紹介した、Base-rate neglectやConjunction Fallacyはまさにそうです。
有限サンプリングでは確率空間全体が把握できないので、ある事象のBase-rateを計算することは困難です (=> Base-rate neglect)。また、サンプリング開始点から遠い事象の確率に関する情報は未開拓になりやすく、その上得られたサンプルは自己相関しているため、独立した複数の確率を比較することも困難です (=> Conjunction Fallacy)。
人生は"Good-enough"な解が見つかれば意外となんとかなる件
不確実な世界で最適な行動をするためには、もちろん脳がきちんと確率分布を計算できるに越したことはありません。ではどうして脳は、サンプリングという不完全なアルゴリズムに頼っているのでしょうか。もちろん、生物学的に記憶・計算コストを増やしたくないということもあるでしょうが、認知科学的にはもう1つ、Satisficingという言葉があります。
Satisficingとは、最適解を探し続けるよりも、「まぁこれでいいっしょ」という**"Good-enough"な解を見つけるように人や動物の認知機能はできている**、という考え方です。
恋愛がいい例かもしれません。日本の20、30歳代の人口はざっと2500万人なので、日本人だけでも約1000万人は結婚相手候補がいるわけです。外国人も含めればもーっと候補はいます。それでも、結婚した人で、結婚前に付き合った人数が2桁に届く人はほとんどいないのではないでしょうか(たぶん汗)。当然ですが、1人しか選べない制約があるので、本当に一番自分に合う人を見つけたければその1000万人+と付き合わなければいけません。が、そんなことをしていては結婚する前に天寿を全うしてしまうのが目に見えているので、脳は恋愛というSatisficingのシステムを採用しています。つまり、この人以外考えられない!好き!愛している!という、本来は自分の子供に愛着を持ち、生存させるための愛情という感情を、遺伝的相補性と類似性がある程度見込まれる以外は全くの他人に向けさせることで、あなたの脳はあなたに他の最適解が含まれるかもしれない可能性の全てを無視させ、Good-enoughな解(相手)と子孫を残させようとしているのですね。
このSatisficing仮説が正しければ、脳がベイジアンサンプリングを採用しているのもうなずけます。比較的単純なアルゴリズムで、完全に確率分布を表象するのはできないけれども、近似はできるのですから。
その結果として、日によってばらばらのことを言っていたり (サンプリングのランダム性)、同じような過ちを何度も繰り返しちゃったって(自己相関)、大抵はそんな大きな問題にはならないですよね。いいじゃないですか。そのためにみんないるんですから。心理学の世界にはWisdom of crowdsという言葉があります。1人の専門家の意見よりも、複数の素人の意見を平均した方がよい結果につながりやすい、という経験則です。どんなに勉強したって、脳を持った人間である以上サンプリングの罠からは逃れられないんです。だから人は集まって、意見を交わして、どうするか決めているのですね。一見無駄に見えるかもしれませんが、きっとそれでいいんです。だってIt is good-enough!笑
まとめのまとめ
- 脳はベイジアンだが、具体的な確率計算はしていないかもしれない
- そのかわり、ベイジアンサンプリングをしている模様
- ベイジアンサンプリングは、Base-rate neglect、Conjunction fallacyといった人の認知傾向を説明できる
終わりに
脳科学の世界でも、例えば脳の内的な状態(覚醒など)の移り変わりをParticle filterによる複数のサンプリングによって説明する試みもされているようです。AIに関しては、古くはBoltzmann machine、新しいものだとDeep brief networksは、サンプリングを用いたNeural Networkのアプローチをしています。(心理学が文系に分類されている)日本だとあまり学ぶところはありませんが、認知科学は脳科学とAI研究をブリッジする、面白い学問だと思います。
引用
- Sanborn, A. N., & Chater, N. (2016). Bayesian Brains without Probabilities. Trends in Cognitive Sciences. https://doi.org/10.1016/j.tics.2016.10.003
メトロポリス・ハスティング法の例を示すコード
# -*- coding: utf-8 -*-
"""
Reproducing similar figures to Sanborn & Charter, Trends in Cognitive Science 2016.
As a Bayesian sampling, a simple Metropolis-Hastings algorithm is implemented.
"""
# libraries ------------------------------
import numpy as np
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
# %%
# functions -----------------------------
def target_params(disttype):
"""preset parameters for target distributions"""
if disttype == 'round':
me = np.array([2,2])
cov = np.array([[1,0],[0,1]])
elif disttype == 'correlated':
me = np.array([2,2])
cov = np.array([[1,0.9],[0.9,1]])
elif disttype == 'close_bimodal':
me = np.array([[0,0],[4,4]])
cov = np.array([[1,0],[0,1]])
elif disttype == 'bimodal':
me = np.array([[0,0],[10,10]])
cov = np.array([[1,0],[0,1]])
return me, cov
def target_rvs(N, disttype):
"""random samples from target distribution (bivariate Gaussian)"""
me, cov = target_params(disttype)
if disttype in ['round', 'correlated']:
p = multivariate_normal(mean=me, cov=cov).rvs(size=N, random_state=1220).T
return p[0], p[1]
elif disttype in ['bimodal', 'close_bimodal']:
p1 = multivariate_normal(mean=me[0], cov=cov).rvs(size=round(N/2), random_state=1220).T
p2 = multivariate_normal(mean=me[1], cov=cov).rvs(size=N-round(N/2), random_state=1220).T
return np.hstack((p1[0],p2[0])), np.hstack((p1[1],p2[1]))
def kde2D(x, y, bandwidth, xbins=100j, ybins=100j, **kwargs):
"""Build 2D kernel density estimate (KDE)"""
# create grid of sample locations (default: 100x100)
xx, yy = np.mgrid[x.min():x.max():xbins,
y.min():y.max():ybins]
xy_sample = np.vstack([yy.ravel(), xx.ravel()]).T
xy_train = np.vstack([y, x]).T
kde_skl = KernelDensity(bandwidth=bandwidth, **kwargs)
kde_skl.fit(xy_train)
# score_samples() returns the log-likelihood of the samples
z = np.exp(kde_skl.score_samples(xy_sample))
return xx, yy, np.reshape(z, xx.shape)
def target_pdf(p, disttype):
"""target distribution (bivariate Gaussian)"""
me, cov = target_params(disttype)
if disttype == 'round' or disttype == 'correlated':
prob = multivariate_normal.pdf(p, mean=me, cov=cov)
elif disttype == 'bimodal' or disttype == 'close_bimodal':
prob0 = multivariate_normal.pdf(p, mean=me[0], cov=cov)
prob1 = multivariate_normal.pdf(p, mean=me[1], cov=cov)
prob = max([prob0, prob1])
return prob
def proposal_pdf(p):
"""proposal distribution"""
return (p[0] + np.random.normal(0, 1), p[1] + np.random.normal(0, 1))
def mh(N, disttype):
"""metropolis hastings sampling (no 'thin' and 'burn_in' for simplicity)"""
xs = np.array([])
ys = np.array([])
pos_now = (0,0)
accept = 0
for i in range(N):
pos_cand = proposal_pdf(pos_now)
prob_stay = target_pdf(pos_now, disttype)
prob_move = target_pdf(pos_cand, disttype)
if prob_move / prob_stay > np.random.uniform(0,1,1):
pos_now = pos_cand
xs = np.append(xs, pos_now[0])
ys = np.append(ys, pos_now[1])
accept += 1
return xs, ys, accept/N
# %%
# visualization similar to the Fig 1b in Sanborn & Charter 2016 -----------
# preset parameters
disttype = ['round', 'correlated', 'close_bimodal', 'bimodal']
axisrange = [[-2, 6], [-2, 6], [-4, 9], [-4, 14]]
plt.close('all')
# probability distributions
fig1, axes1 = plt.subplots(1, 4)
for i in range(4):
x, y = target_rvs(5000, disttype[i])
xx, yy, zz = kde2D(x, y, 1)
axes1[i].pcolormesh(xx, yy, zz)
axes1[i].set_title(disttype[i])
axes1[i].set_xlabel('x')
axes1[i].set_ylabel('y')
axes1[i].get_xaxis().set_ticks([])
axes1[i].get_yaxis().set_ticks([])
axes1[i].get_xaxis().set_ticklabels([])
axes1[i].get_yaxis().set_ticklabels([])
# iterations & MH samples
fig2, axes2 = plt.subplots(2, 4)
fig3, axes3 = plt.subplots(1, 4)
for i in range(4):
# sampling
xs, ys, accept_ratio = mh(1000, disttype[i])
# iteration
axes2[0,i].plot(np.arange(len(xs)), xs, '-ko', alpha=0.2)
axes2[0,i].set_title(disttype[i])
axes2[1,i].plot(np.arange(len(ys)), ys, '-ko', alpha=0.2)
axes2[1,i].set_xlabel('iteration')
axes2[0,i].set_ylabel('x')
axes2[1,i].set_ylabel('y')
axes2[0,i].get_xaxis().set_ticks([])
axes2[0,i].get_yaxis().set_ticks([])
axes2[0,i].get_xaxis().set_ticklabels([])
axes2[0,i].get_yaxis().set_ticklabels([])
axes2[0,i].set_ylim(axisrange[i][0], axisrange[i][1])
axes2[1,i].get_xaxis().set_ticks([])
axes2[1,i].get_yaxis().set_ticks([])
axes2[1,i].get_xaxis().set_ticklabels([])
axes2[1,i].get_yaxis().set_ticklabels([])
axes2[1,i].set_ylim(axisrange[i][0], axisrange[i][1])
# sampling distributions
axes3[i].scatter(xs, ys, s=20, c='k', alpha=0.2)
axes3[i].set_title(disttype[i])
axes3[i].set_xlabel('x')
axes3[i].set_ylabel('y')
axes3[i].set_xlim(axisrange[i][0], axisrange[i][1])
axes3[i].set_ylim(axisrange[i][0], axisrange[i][1])
axes3[i].get_xaxis().set_ticks([])
axes3[i].get_yaxis().set_ticks([])
axes3[i].get_xaxis().set_ticklabels([])
axes3[i].get_yaxis().set_ticklabels([])
fig2.tight_layout()
fig3.tight_layout()