概要
- 直感的にはロジスティック回帰の損失関数としてMSEが使えそうだが、クロスエントロピーが使われてるのはなぜなのか
- 損失関数の凸性を考えたら分かりやすい
- 結局、ロジスティック回帰ではクロスエントピーがよい
損失関数の凸性
機械学習において、目的関数のが凸性(convexity)を持つことは極めて重要である。なぜなら局所最適解$\implies$大域最適解を満たし、安定した学習を保証するためである。
凸性とは
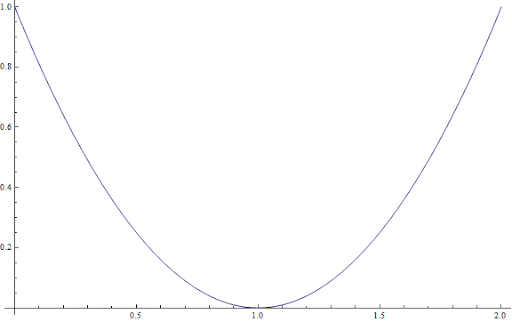
直感的理解 : 下側に綺麗にもっこりしている様
こんな感じ↓
ちゃんとした定義 :
関数$f : X \to R$に対して
$$f(\lambda x_1 + (1 - \lambda) x_2) \leq \lambda f(x_1) + (1 - \lambda) f(x_2), \ \\ \forall x_1,x_2 \in X, \ \forall \lambda \in [0,1]$$
凸性とヘッシアン
ある関数が上記の定義を満たすかどうかを評価するのにヘッシアンを用いる
おさらいするとヘッシアンとは関数の二階偏微分を持つ行列で$(i,j)$成分に$\frac{\partial f}{\partial x_i \partial x_j}$を持つため対称行列となる。
一般に
ある関数のヘッシアンが半正定値($positive \ semidefinite$)行列であることとその関数が凸関数であることは同値
"行列の(半)正定値性"
行列$M$が任意のベクトル$x \in X^d$に対して$$x^*Mx >(\geq)\ 0$$となる時、Mは(半)正定値行列
ここで言っているのは$x$と$Mx$の内積が正もしくは0以上になることであり、直感的にこれは$M$が$x$の向きを大きく変えずに保持していることを意味する。
単一変数関数の場合は2階微分が正(0以上)であることに単純化できる
ロジスティック回帰におけるMSEのヘッシアン
パラメータ$w$を持つ予測器$f : X \to R$に対して損失関数$l(x)$は
$$l(x) = (y - \widehat{y})^2$$
$$where \ \ \ \widehat{y} = \sigma(w^Tx) = \frac{1}{1 + e^{w^Tx}}$$
その微分
$$\frac{\partial l(x)}{\partial w} = -2(y - \widehat{y})\frac{\partial \widehat{y}}{\partial w}$$
$$= -2(y - \widehat{y})(1 - \widehat{y})\widehat{y}x \ \ \because \frac{\partial \widehat{y}}{\partial w} = (1 - \widehat{y})\widehat{y}x$$
$$ = -2(y\widehat{y} - y\widehat{y}^2 - \widehat{y}^2 + \widehat{y}^3)x$$
ヘッシアンは
$$\frac{\partial^2 l(x)}{\partial w^2} = \frac{\partial l(x)}{\partial \widehat{y}} \frac{\partial \widehat{y}}{\partial w}$$
$$= -2(y - 2y\widehat{y} - 2\widehat{y} + 3\widehat{y}^2)x(1 - \widehat{y})\widehat{y}x$$
$$\therefore H(\widehat{y}) = -2(3\widehat{y}^2 - 2\widehat{y}(1 + y) - y)x^2$$
$y=0$のとき
$$H(\widehat{y}) = -2(3\widehat{y}(\widehat{y} - \frac{2}{3}))x^2$$
$y=1$のとき
$$H(\widehat{y}) = -2(3(\widehat{y} - \frac{1}{3})(\widehat{y} - 1))x^2$$
両場合において、$0\leq\widehat{y}\leq1$より、ヘッシアンは必ずしも常に0以上ではないことは明らか。つまり、$l(x)$は凸関数ではない
ロジスティック回帰におけるクロスエントロピー損失のヘッシアン
損失関数
$$l(x) = -y \log(\widehat{y}) - (1 - y) \log((1 - \widehat{y}))$$
変形(詳細省略)
$$-l(x) = \log(1 + e^{wx}) - xyw$$
微分
$$\frac{\partial l(x)}{\partial w} = \frac{1}{1 + e^{wx}} x e^{wx} - xy$$
$$= \frac{x}{1 + e^{-wx}} - xy$$
ヘッシアン
$$H(x) = x \frac{-1}{(1 + e^{-wx})^2} e^{-wx} (-x)$$
$$= \frac{e^{-wx}}{(1 + e^{-wx})^2} x^2 \geq 0$$
上記よりクロスエントロピーの場合はヘッシアンは常に0以上となり損失関数が凸になる。
まとめ
- ロジスティック回帰において直感的にはMSEが使えそうな気がするが関数の凸性を考えてあげると使えない理由がわかる。
- ロジスティック回帰においてMSEは凸ではない。
- ロジスティック回帰においてクロスエントロピー損失はいかなる入力に対しても常にヘッシアンが0以上になり、凸性が保証されている。
取り急ぎまとめたので、誤りなどあればお気軽にコメントください。早急に修正いたします。
reference