「新・明解Pythonで学ぶアルゴリズムとデータ構造」で勉強日記#5~8(第2章まとめ)

2章まとめ
【出典】「新・明解Pythonで学ぶアルゴリズムとデータ構造」

「新・明解Pythonで学ぶアルゴリズムとデータ構造」で勉強日記#5

2-1データ構造と配列

最初はデータ構造や配列とはなんぞやというところから始めるみたいですね。

配列の必要性

急に配列の必要性なんて言われても…。そもそも配列がピンとこない私には話が飛躍している気がするので…。

配列：コンピューターのプログラミング言語における、データ形式の一。同じ型のデータの集合を意味し、個々のデータは変数の添え字で区別する。【出典】デジタル大辞泉

とのことでした。

以下のプログラムでは5人の生徒の点数を合計した値、平均した値を求めます。

list2-1

#5人の点数を読みこんで、合計・平均点を表示

print('5人の点数の合計点と平均点を求めます。')

tensu1 = int(input('1番目の点数:'))
tensu2 = int(input('2番目の点数:'))
tensu3 = int(input('3番目の点数:'))
tensu4 = int(input('4番目の点数:'))
tensu5 = int(input('5番目の点数:'))

total = 0
total += tensu1
total += tensu2
total += tensu3
total += tensu4
total += tensu5

print(f'合計は{total}点です。')
print(f'平均は{total / 5}点です。')

さて、上記のコードでは、応用の利かない記述になっていることは明確です。
①人数を可変、②特定の点数を調べる/書き換え、③最低点と最高点を求める/ソートの3つを実現することで、有用性のあるプログラムといえます。そのためにはプログラムの作り方を変える必要があります。

まず、各生徒の点数をひとまとめにして扱えるようにします。それを実現するのが配列と呼ばれるデータ構造です。

配列はオブジェクトの格納庫であって格納された個々の変数は要素と呼ばれます。各要素には先頭から順番に0,1,2・・・の添字が与えられる。

配列は生成時に要素を自由に指定できるため①はクリアできます。また、要素数の増減も可能です。添字を使った式（tensu[2]など）でアクセスできるため②の実現も容易。ここの要素を自由にアクセスできる結果として③も実現できます。

こうやって考えると配列の考えは重要でプログラミングには欠かせないものということがわかりました。

#リストとタプル
pythonで配列を実現するのがリストとタプルです。いずれも高機能なデータのコンテナ（格納庫）です。
リスト：変更可能（ミュータブル）なlist型のオブジェクト。list関数を使うと文字列やタプルなど様々な型のオブジェクトをもとに、リストを生成できます。要素数が決まっており、要素の値は未定（空の情報）の時 None を使うことが可能。[]を使う。

タプル：組とも呼ばれる。要素を順序付けて組み合わせたもの。変更不能（イミュータブル）オブジェクトで、tuple型。()を使う。

単一の値であってタプルではない値

v01 = 1　#1
v02 = (1) #1

アンパック：リストから要素の一括取り出しができる。

例2-1リストから要素の一括取り出し

x = [1, 2, 3]
a, b, c = x
print(a,end = '')
print(b,end = '')
print(c,end = '')

#インデックス式によるアクセス
リストやタプル内の個々の要素をアクセスする際のキーとなるのが、インデックス。
   [1,2,3,4,5,6,7]
先頭0 1 2 3 4 5 6 末尾（非負のインデックス）
先頭-7-6-5-4-3-2-1末尾（負のインデックス）

インデックス式

例2-2リストとインデックス式

x = [11, 22, 33, 44, 55, 66, 77]
print(x[2])

print(x[-3])

x[-4] = 3.14 #要素の置換
print(x)

代入でコピーされるのは値でなく参照であるため、x[-4]の参照先がint型(44)からfloat型(3.14)に変わります。
なお、xがタプルだった場合は代入はエラーになります。（タプルは変更不能なため）

存在しないインデックス

x[7] #存在しないインデックスの値は取り出せない

x[7] = 3.14 #存在しないインデックスへの代入による要素の追加は行われない

存在しない要素をアクセスするインデックス式を、左辺に置く代入によって、要素が新しく追加することはできません。

#スライス式によるアクセス
スライス：リストやタプル内の部分を連続あるいは一定周期で新しいリストあるいはタプルとして取り出すこと

スライス式による取り出し
s[i:j] ・・・s[i]からs[j-1]までの並び
s[i:j:k] ・・・s[i]からs[j-1]までのkごとの並び

例2-3

s = [11, 22, 33, 44, 55, 66, 77]
s[0:6]

s[0:7]

s[0:7:2]

s[-4:-2]

s[3:1]

・iとjは、len(s)よりも大きければ、len(s)が指定されたものとみなされる。
インデックスとは異なり、正当な範囲外の値を指定してもえらーとならない。
・iが省略されるかNoneであれば、0が指定されたものとみなされる。
・jが省略されるかNoneであれば、len(s)がしていされたものとみなされる。

まとめると以下のようになります。
s[:]・・・すべて
s[:n]・・・先頭のn要素
s[i:]・・・s[i]から末尾
s[-n:]・・・末尾の-n要素
s[::k]・・・k-1個おき
s[::-1]・・・すべてを逆向き
※nが要素数を超える場合は全要素が取り出される。

コラム2-1 代入とイミュータブル（変更不能）/ミュータブル（変更可能）

変数には、格納済みの値とは異なる型の値を代入できます。
型にどんな種類があるかわかりませんが、できるそうです。

IDの参照

n = 5
id(n) #5のIDが参照される

n = 'ABC'
id(n)　#ABCのIDが参照される

文字列の代入後にnの識別番号が変わります。（int型からstr型に更新）
変数への代入によってコピーされるのは参照先である識別番号（同一性）であって値ではないため、あらゆる型のオブジェクトを変数に代入できるそうです。
pythonの代入文は極めて多機能で、初めて使う名前の変数に値を代入するだけで、その名前の変数が自動的に用意される。それ以外にも多くの機能があるみたいです。

一括代入

a, b, c =1, 2, 3
print(a)
print(b)
print(c)

ちょっと便利な用例

x = 6
y = 2
x, y = y + 2, x + 3

print(x)
print(y)

累算代入によるインクリメント

n = 12
id(n)

n +=1　#nの値を1増やす
id(n) #識別番号が変更される

聞くだけだとたくさんの機能がある分覚えること多くて大変そうと思いますが、一見すると便利感あります。

型について、int型やstr型はいったん与えられた値が変更できないイミュータブルな型だそうで。（nの値は変更できるが12など数字自体の値（id）は変更できないため）
・ミュータブルな型：リスト、辞書、集合　など
・イミュータブルな型：数値、文字列、タプル　など

pythonの代入の特性
・左辺の変数名が初出であれば、その変数を定義する。
・代入文は、値ではなく参照先（識別番号＝同一性）を代入する。
・複数の代入が一括で可能。

とまとめられています。

具体的な記述で見れば

x + 17 は式。
x = 17 は文。

ということみたいです。

余談ですが、C,C++,javaなどは、　=　は'右結合の演算子'として扱われるため

a = b = 1 は a = (b =1)

という解釈になるらしいです。（こちらの方が数学のイメージに近いですね）

pythonでは、= は演算子でないため、結合性は存在しません。

#データ構造
データ構造：構成要素との間に何らかの相互関係をもつデータの論理的な構成のこと。（つまり複数のデータが集まった構造だが、0個、1個もありうる）

イメージをしようと思うと結構難しいので私は「へー」程度の理解にしておこうと思います。

コラム2-2リストとタプル（その１）

リストやタプルの長さを表示

x = [15, 64, 7, 3.14, [32, 55], 'ABC'] 
len(x) #[32, 55]は１つとしてカウントされる

min()やmax()はリストやタプルも引数として渡すことができる。

y = [2, 4, 5, 78, 98 ]
print(min(y))
print(max(y))

空リスト/空タプルの判定
空リスト、空タプルの判定は偽になります。

EX

z = []

if z:
    print("True")
else:
    print("False")

z = []

if not z:
    print("True")
else:
    print("False")

値比較演算子による大小関係および等価性の判定
リストどうし/タプルどうしの大小関係および等価性の判定は、値比較演算子によって行えます。
次に示すのはいずれも真となる判定の例。

真となる判定の例

[1, 2, 3] == [1, 2, 3]

[1, 2, 3] < [1, 2, 4]

[1, 2, 3, 4] <= [1, 2, 3, 4]

[1, 2, 3] < [1, 2, 3, 5]

[1, 2, 3] < [1, 2, 3, 5] < [1, 2, 3, 5, 6]

インデックスが同じところどうしで判定が行われていき、条件が合えばTrueを返すようですね。

リストとタプルの共通点と相違点
リストとタプルの相違点は次の表のようになるようです。

Table 2C-1

性質/機能	リスト	タプル
ミュータブル	〇	×
辞書のキーとして利用できる	×	〇
イテラブルである	〇	〇
帰属性演算子in演算子/not in 演算子	〇	〇
加算演算子＋による連結	〇	〇
乗算演算子＊による繰り返し	〇	〇
累算演算子＋＝による連結代入	〇	△
累算＊＝による繰返し代入	〇	△
インデックス式	〇	△
スライス式	〇	△
len関数による要素数取得	〇	〇
min関数/max関数による最小値/最大値	〇	〇
sum関数による合計値	〇	〇
indexメソッドによる探索	〇	〇
countメソッドによる出現回数	〇	〇
del文による要素の削除	〇	×
appendメソッドによる出現回数	〇	×
clearメソッドによる全要素の削除	〇	×
copyメソッドによるコピー	〇	×
extendメソッドによる拡張	〇	×
insertメソッドによる要素の挿入	〇	×
popメソッドによる要素の取り出し	〇	×
removeメソッドによる指定値の削除	〇	×
reverseメソッドによるインプレースな反転	〇	×
内包表記による生成	〇	×
コラム2-3へ続く・・・

以上で2章1節のお話が終わります。リストとタプルの使い分けとかいまいちわからんなあと思っているので、追々理解できたらいいなと思います。

「新・明解Pythonで学ぶアルゴリズムとデータ構造」で勉強日記#6

2-2配列

いよいよリストやらタプルやらの使い方がわかりそうな予感がします。
今まで、どうやって活用すればいいのかわかっていなかったので楽しみです。

配列の要素の最大値を求める

最初に、配列の要素の最大値を求める手続きを考えるようです。
配列aの要素が4個として、三つの要素a[0], a[1], a[2], a[3]の最大値を、以下のプログラムで求めます。

a = [22, 57, 11, 91]
maximum = a[0]
if a[1] > maximum: maximum = a[1]
if a[2] > maximum: maximum = a[2] #要素数が3であればif文を2回実行
if a[3] > maximum: maximum = a[3] #要素数が4であればif文を3回実行

maximum

まず、配列の要素数とは無関係に、先頭要素a[0]の値をmaximumに代入する作業を行い、その後if文を実行する過程で必要に応じてmaximumの値を更新します。
要素数がnであれば、if文の実行は、n-1回必要で、その際、maximumとの比較やmaximumへの代入の対象となる添字（インデックスのことで、以後統一）は、1,2,・・・と増えていきます。
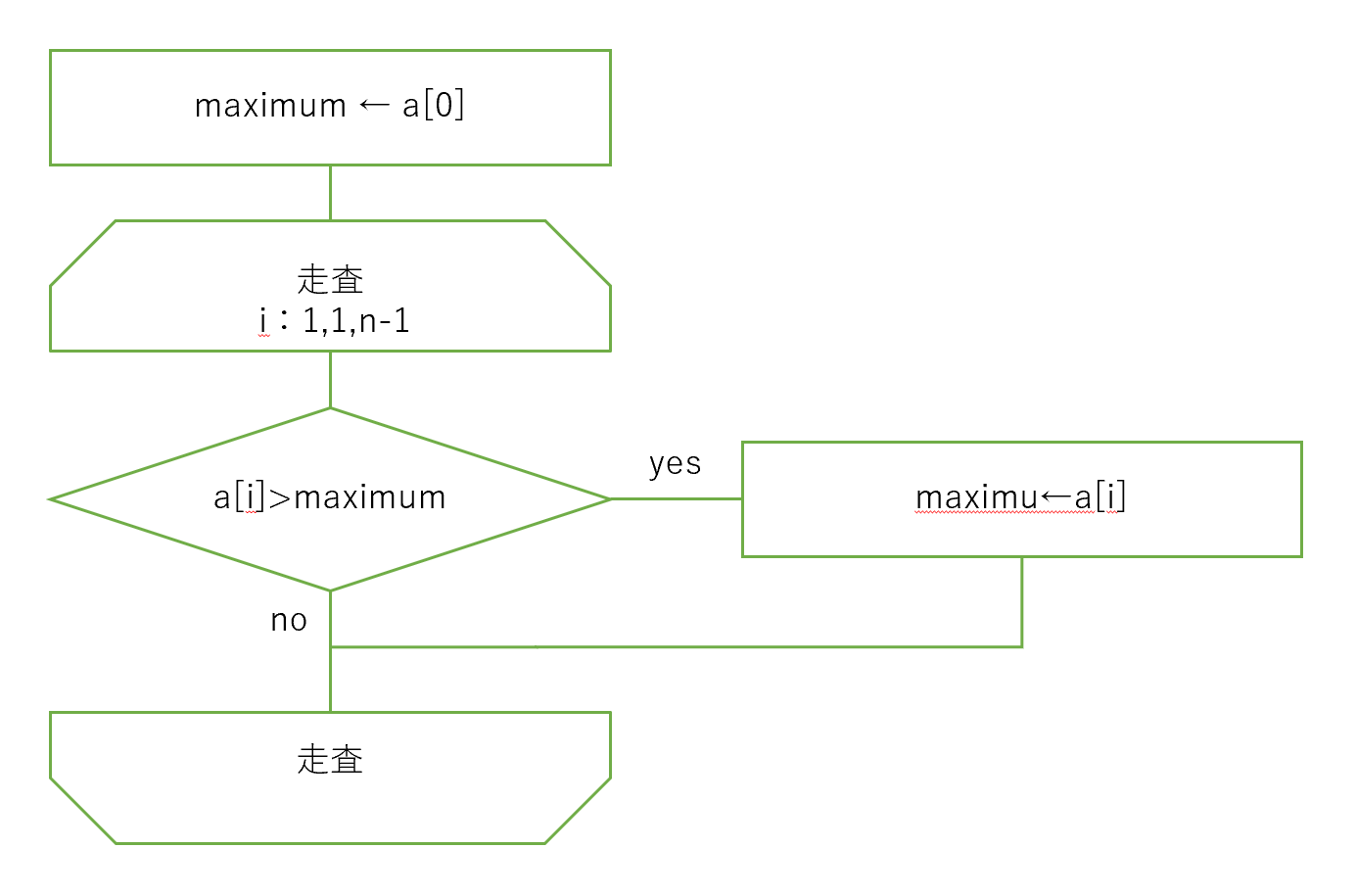
そのため、配列aの要素の最大値を求めるアルゴリズムのフローチャートは次のようになります。

このアルゴリズムに基づいて、配列aの要素の最大値を求める関数の関数定義と、その関数によって最大値を求める様子を配列の要素数が5としたとき

def max_of(a):
    maximum = a[0]
    for i in range(1, len(a)):
        if a[i] > maxmum:
            maximum = a[i]

という関数を定義し、最大値を求めることができます。

仮に[22, 57, 11, 91, 32]という配列があったとき
22>57 → 57
57>11 → 57
57>91 → 91
91>32 → 91
となことがわかります。
リストの表記（s[]←こういうやつ）に慣れが必要だなと感じますが、今回の記事を通して、少しでも慣れることがで切ればいいなと思います。（記号が多いと頭の整理が必要ですよね。）
（余談ですが本書の流れに沿ている都合で関数定義をしています。）

配列の要素の最大値を求める関数の実装

関数の”実装”というとなんか難しい感じがしますが、関数を定義して使うという解釈でいいのかな？

list2-2

#シーケンスの要素の最大値を表示する
from typing import Any,Sequence

#max_ofの定義
def max_of(a: Sequence) -> Any:
    '''シーケンスaの要素の最大値を表示する'''
    maximum = a[0]
    for i in range(1, len(a)):
        if a[i] > maximum:
            maximum = a[i]
    return maximum

#関数max_ofをテストする

if __name__ == '__main__':
    print('配列の最大値を求めます。')
    num = int(input('要素数：'))
    x = [None] * num #要素数numのリストを生成
    
    for i in range(num):
        x[i] = int(input(f'x[{i}]:'))
        
    print(f'最大値は{max_of(x)}です。')

急に複雑になるやつ…。とりあえず定義のところは分かりますが、急に->みたいな記号使われると頭がパニックです。
意味としてはaのシークエンスの型はなんでも対応します的なニュアンスでいいですかね？
ということで次で解説してくれています。

#アノテーションと型ヒント
まずは、プログラムの先頭行
from typing import Any,Sequence
に着目します。

このインポートによって、AnyとSequenceが単純名で利用できるようになるそうです。
Anyは制約のない(任意の)型であることを表し、Squenceはシーケンス型を表します。
シーケンス型にはlist型,bytearray型,str型,tupple型,bytes型がある(つまり連続的なイメージでいいですか？)ため、関数max_ofの関数頭部のアノテーション(特定のデータに対して情報タグ(メタデータ)を付加することらしい【出典】デジタル大辞泉)は次の表明を行うことになります。
・受け取る仮引数aの型として、シーケンス型であることを期待する。
・返却するのは任意の型である。
以上より関数max_ofは次のような特性を持ちます。
・関数内では、配列aの要素の値は変更しない。
・呼び出し側が与える実引数の型は、変更可能なリスト、変更不能なタプルや文字列など、シーケンスであれば何でもよい。
・呼び出し側が与えるシーケンスの要素としては、値比較演算子＞で比較可能でさえあれば、異なる型（int型float型）が混在してもよい。
・最大の値の要素を返却する（最大の値の要素がint型の要素であればint型の値を返却し、float型の要素であればfloat型を返却する。）
なお、関数内で要素の値を変更する配列型の仮引数に対するアノテーションは、Sequenceではなく、MutableSequenceとしなければならない。
※その場合、実引数として、ミュータブルリストは与えられるが、イミュータブルな文字列型、タプル型、バイト列型の実引数は与えられなくなる。
文字ばかりでわかりづらいですが、つまるところいろんな型に対応できますよということですかね？

再利用可能なモジュールの構築

pythonでは単一のスクリプトプログラムがモジュールとなります。
拡張子.pyを含まないファイル名がそのままモジュール名となるため、本プログラムのモジュール名はmaxになります。

これ、関数の勉強してたときなんかに既成ファイルから引っ張れるぜってところまでは知っていたのですが、自分で作れるんだあと思って夢が広がりました。
じゃあライブラリとかも最初に作った人がいてくれたおかげで楽な記述ができるんだと思うと頭が上がらないですね。（ほかの言語とかもやっぱりそういうのあるのかな？）

さて、本プログラム後半のif文では__name__と'__main__'の等価性が判定されています。
左オペランドの__name__はモジュールの名前を表す変数であり、次のように決定されます。

スクリプトプログラムが：
・直接実行されたとき　変数__name__は'__main__'
・インポートされたとき 変数__name__は本来のモジュール名（今回の場合はmax）

pythonはすべてをオブジェクトとみなすため、モジュールもオブジェクトとなります。(初耳ですわ)
モジュールは、別のプログラムから初めてインポートされたタイミングで、そのモジュールオブジェクトが生成・初期化される仕組みになっています。
そのため、プログラム後半のif文の判定は、'max.py'を直接起動したときのみ真とみなされif __name__ == '__main__':以下のコードが実行されるそうです。つまりほかのファイルから読み込んだときは動かないということですね。(実装イメージがまだできないけど)
ほかのスクリプトプログラムからインポートされたときは偽とみなされるためif __name__ == '__main__':以下は実行されない。
※モジュールオブジェクトの中には、__name__のほかにも、__loader__、___package__、__spec__、__path__、__file__などの変数(属性)が入っている。

急に出てきて！？ってなりますが、ちゃんと抑えれば怖くないですね。とりあえず便利な機能程度に今は覚えておきます…。()

モジュールのテスト

list2-2のモジュール'max'で定義された関数'max_of'をほかのスクリプトプログラムから呼び出してみる。
値の読み込み時に要素数を決定する
list2-3はキーボードからint型の整数値を次々と読み込んでいき、終了が指示されたら('End'と入力されたら)読み込みを終了する(その時点で要素数が確定する)ように実現したプログラムです。
※本プログラムを含め、関数'max_of'を呼び出すプログラムは、'max.py'と同一フォルダに格納する必要がある。

list2-3

#max_of_test.py

#配列の要素の最大値を求めて表示(要素の値を読み込む)

from max import max_of

print('配列の最大値を求めます。')
print('注："End"で入力終了。')
      
number = 0
x = [] #空リスト

while True:
      s = input(f'x[{number}]:')
      if s == 'End':
          break
      x.append(int(s)) #末尾に追加
      number += 1

print(f'{number}個読み込みました。')
print(f'最大値は{max_of(x)}です。')

'from max import max_of'はモジュールmaxで定義されている'max_of'を単純名で利用できるようにするためのimport文。
プログラムでは、まず最初にリストxを、空の配列(空リスト)として生成しています。
while文は無限ループであり、次々と文字列を読み込む。読み込んだ文字列がEndであれば、break文の働きによってwhile文を強制終了する。
読み込んだ文字列sが'End'出ない場合は読み込んだ(文字列sをint関数によって変換した)整数値を、配列xの末尾に追加する。
変数numberは0で初期化され、整数値を読み込むたびにインクリメントされるため、読み込んだ整数値の個数(配列xの要素数と一致する)が保持される。
※インポートするモジュール'max.py'の'max_of'以外は__name__ == '__main__'が成立しないためif __name__ == '__main__':以下の文は実行されない。(アンダーバーが消えてるので注意。出し方わからんです。)

配列の要素の値を乱数で決定する

配列の要素はキーボードから読み込み、全要素の値は乱数で決定する。

list2-4

#配列の要素の最大値を求めて表示(要素の値を乱数で生成)

import random
from max import max_of

print('乱数の最大値を求める')
num = int(input('乱数の個数：'))
lo = int(input('乱数の下限：'))
hi = int(input('乱数の上限：'))
x = [None] * num #要素数numのリストを生成

for i in range(num):
    x[i] = random.randint(lo, hi)
    
print(f'{(x)}')
print(f'最大値は{max_of(x)}です。')

ここで、「おー」と思ったのは空リストの生成ですね。Noneとかなかなかうまく使えないので、こういう例があると助かります。

タプルの最大値/文字列の最大値/文字列のリストの最大値を求める

list2-5はタプルの最大値、文字列(内の文字)の最大値/文字列のリストの最大値を求めるプログラム

list2-5

#配列の要素の最大値を求めて表示(タプル/文字列/文字列のリスト)

from max import max_of

t = (4, 7, 5.6, 2, 3.14, 1)
s = 'string'
a = ['DTS', 'AAC', 'FLAC']

print(f'{t}の最大値は{max_of(t)}です。')#7
print(f'{s}の最大値は{max_of(s)}です。')#t
print(f'{a}の最大値は{max_of(a)}です。')#FLAC

文字列のみの場合は文字コード、文字列リストの場合は文字列の数で判定される…。なんか面白いことできそうな…。？？

list2-5(max/min)

#配列の要素の最大値を求めて表示(タプル/文字列/文字列のリスト)max,min関数を使用

t = (4, 7, 5.6, 2, 3.14, 1)
s = 'string'
a = ['DTS', 'AAC', 'FLAC']

#最大値
print(f'{t}の最大値は{max(t)}です。')#7
print(f'{s}の最大値は{max(s)}です。')#t
print(f'{a}の最大値は{max(a)}です。')#FLAC
#最小値
print(f'{t}の最小値は{min(t)}です。')#1
print(f'{s}の最小値は{min(s)}です。')#g
print(f'{a}の最小値は{min(a)}です。')#AAC(文字列の数、文字コードの順で検索される)

コラム2-3 リストとタプル(その２)

前回出てきたコラムの続きですね。

別々に生成されたリスト/タプルの同一性

別々に生成されたリストはすべての要素が同じ値をもっていても、別の実体を持つ。

list1 = [1,1,1]
list2 = [1,1,1]
print(list1 is list2)
print(list1 is list1)

[1,1,1]は[]演算子によって新しいリストを生成する式であり、いわゆるリテラル(直接記述される数値や文字列)ではない。

つまり、式であることを認識できていれば大丈夫ですかね。なんか前にちらっと触れていた気もしますが忘れたのでまた復習します。

リスト/タプルの代入

リスト（を参照している変数）を代入しても、値でなく参照がコピーされるため、要素自体（要素の並び）はコピーされない。

参照の確認

lst1 = [1,1,1]
lst2 = lst1
print(lst1 is lst2)

lst1[2] = 9
print(lst1)
print(lst2)#lst1を参照している。

is関数なんてあるんですね。
Excelなんかでも真偽判定の重要性は思い知ったので、こういう使い方できる情報はありがたいです。

リストの走査
リストを走査する4種類のプログラムを下記に示してます。

list2C-1

#リストの全要素を走査（要素数を事前に取得）
x = ['john', 'geoge', 'paul', 'ringo']#[]を()にするとタプルになる

for i in range(len(x)):
    print(f'x[{i}] = {x[i]}')
print('_'*13)

list2C-2

#リストの全要素をenumerate関数で走査
x = ['john', 'geoge', 'paul', 'ringo']

for i,name in enumerate(x):
    print(f'x[{i}] = {name}')
print('_'*13)    

i, nameを使うことで、enumerate関数を使って同じ出力ができます。

list2C-3

#リストの全要素をenumerate関数で走査(1からカウント)
x = ['john', 'geoge', 'paul', 'ringo']

for i,name in enumerate(x, 1):
    print(f'{i}番目 = {name}')
print('_'*13)    

enumerate(x, 1)とすることで、カウントの開始を1にします。(0～3が1～4に代わる)

list2C-4

#リストの全要素を走査(インデックス値を使わない)

x = ['john', 'geoge', 'paul', 'ringo']

for i in x:
    print(i)

また、インデックスの値が不要な場合は簡素に書くこともできます。

・イテラブル
文字列、リスト、タプル、集合、辞書などの型をもつオブジェクトは、いずれもイテラブル＝反復可能である'という共通点があります。
イテラブルオブジェクト（リストなど）を組み込み関数であるiter関数に引数として与えるとそのオブジェクトに対するイテレータが返却されるそうです。
イテレータ：データの並びを表現するオブジェクト。
イテレータの__next__メソッドを呼び出すか、組み込み関数であるnext関数にイテレータを与えるとその並びの要素が順次取り出される。取り出すべき要素が尽きた場合はStopIteration例外が送出されるとのこと。

iter/next関数の例

x = ['john', 'geoge', 'paul', 'ringo']

t = iter(x)
while True: #Trueの間繰り返す
    try: #例外処理(例外が発生したときに処理する)
        print(next(t))
    except StopIteration: #except エラー名
        break #StopIterationが出たらループ終了

エラーが出たときに処理が行われるという。便利そうなやつですね。

「新・明解Pythonで学ぶアルゴリズムとデータ構造」で勉強日記#7

配列の要素の並びを反転する

配列の要素の並びを反転するプログラムを考えます。
[1, 2, 3, 4, 5, 6, 7]という配列があるとすると
1,7
2,6
3,5
のペアをそれぞれ入れ替えることを考えると次のようなアルゴリズムになります。
for i in range(n//2):
a[i](左側の要素の添字)とa[n-i-1](右側の要素の添字)の値を交換します。

list2-6

#ミュータブルなシーケンスの要素の並びを反転

from typing import Any, MutableSequence

def reverse_array(a: MutableSequence) -> None:
    '''ミュータブルなシーケンスaの要素の並びを反転'''
    n = len(a)
    for i in range(n // 2):
        a[i], a[n - i - 1] =  a[n - i - 1], a[i]

if __name__ == '__main__':
    print('配列の並びを反転します。')
    nx = int(input('要素数は:'))
    x = [None] * nx #要素nのリストを生成
    
    for i in range(nx):
        x[i] = int(input(f'x[{i}]:'))
        
    reverse_array(x) #xの並びを反転
    
    print('配列の要素の並びを反転しました')
    for i in range(nx):
        print(f'x[{i}] = {x[i]}')

反転とか並べ替えとは便利な気はしますが具体的にどのへんで使うんだろうという感じがしてイメージがわかないです…。(未熟故…。)

コラム 2-4リストの反転
先ほどは関数を定義していましたが、メソッドや関数も存在しているみたいです

・リストの反転(標準ライブラリ)
list型のreverseメソッドはインプレース(定位置)に反転する
使用例：x.reverse()
・反転したリストの生成(reversed関数)
使用例：y = list(reversed(x))

基数変換

10進数を2進数にしたりするやつですね。
0～9、A～Zを使って最大36進数まで作れるみたいです。

コラム2-5基数について
a**nという式があるとすれば、aが基数、n+1が桁数になる。
例)1234が10進数の場合
1234 = 1 * (10**3) + 2 * (10**2) + 3 * (10**1) + 4 * (10**0)

基数変換を行うプログラム
list2-7では基数変換を行うプログラムを下記に記述します。

list2-7

#読み込んだ10進数を2進数から36進数に基数変換して表示
def card_conv(x: int, r: int) -> str:
    '''整数値xをr進数に変換した数値を表す文字列を返却'''
    
    d = '' #変換後の文字列
    dchar = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
    n = len(str(x)) #変換前の桁数
    
    print(f'{r:2} | {x:{n}d}')
    while x > 0:
        d += dchar[x % r] #該当文字を取り出して連結
        x //= r
    
    return d[::-1] #反転して返却

if __name__ == '__main__':
    print('10進数を基数変換します。')
    
    while True:
        while True:
            no = int(input('変換する非負の整数：')) #非負の整数値を読み込む
            if no > 0:
                break
                
        while True:
            cd = int(input('何進数に変換しますか(2-36)：'))
            if 2 <= cd <= 36:
                break
        
        print(f'{cd}進数では{card_conv(no, cd)}です。')
        
        retry = input('もう一度しますか（Y…はい/N…いいえ）')
        if retry in {'N', 'n'}:
            break

多重ループが出てきましたね。2 <= cd <= 36のあたりも参考になります( ..)φメモメモ
ちょっと前にやったd[::-1]という表記もありますね。
だいぶ慣れてきた気がします。

さて、このままでは関数内の動きがいまいち見えてこないため、以下のように変更します。

list2-7(基数変換の過程を表示する)

#読み込んだ10進数を2進数から36進数に基数変換して表示
def card_conv(x: int, r: int) -> str: #今回では、xはno,rはcdを参照する
    '''整数値xをr進数に変換した数値を表す文字列を返却'''
    
    d = '' #変換後の文字列
    dchar = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ' #文字列36個
    n = len(str(x)) #変換前の桁数　
    print(f'{r:2} | {x:{n}d}') #f{'r:2(rを2桁で表示)|{x}'}
    while x > 0: #非負の値の間実行
        print('   +' + (n + 2) * '-') #'   +'と'-*(n+2)個'を表示
        if x // r: #xをrで割ることができる場合(最後以外の段の線)
            print(f'{r:2} | {x // r:{n}d} … {x % r}') #f'{r:2} (rを2桁で表示)| {x // r:{n}d(x//rをn桁の10進数で表示)} … {x % r}(x/rの余り)'
        else: #xをrで割ることができない場合(最後の段の線)
            print(f'     {x // r:{n}d} … {x % r}') #f'     (空白){x // r:{n}d}(x//rをn桁の10進数で表示) … {x % r}(x/rの余り)'
        d += dchar[x % r] #該当文字を取り出して連結(0～Zまでの値)(d = d + dchar[x % r]と同じ)
        x //= r #x = x // rと同じ
    
    return d[::-1] #反転して返却


if __name__ == '__main__': #このファイルを動かすときのみ実行
    print('10進数を基数変換します。')
    
    while True: #Trueの間実行
        while True: #Trueの間実行
            no = int(input('変換する非負の整数：')) #非負の整数値を読み込む
            if no > 0: #読み込んだ数字が非負の整数であれば
                break #ループを抜ける
                
        while True: #Trueの間実行
            cd = int(input('何進数に変換しますか(2-36)：')) #数字を読み込む
            if 2 <= cd <= 36: #2から36までの数字であれば
                break　#ループを抜ける
        
        print(f'{cd}進数では{card_conv(no, cd)}です。')#cdと関数card_conv()に数値が代入される
        
        retry = input('もう一度しますか（Y…はい/N…いいえ）')
        if retry in {'N', 'n'}:
            break

処理付きでの結果が見れるようになりました。

自分なりに整理するために細かくコメントをつけてみました。(間違っていたらすみません。)

リストじゃなくて文字列でもリスト的な取出し方ができるんですね。ここでは、簡単な操作しかないからるリストに格納するまでもないということですかね？

だいぶ表記も増えたので、頭がこんがらがりそうですが、一文ずつ見ていけば理解できますね。

コラム2-6 関数間の引数の受け渡し
関数が受け取る仮引数と、呼び出す側が与える実引数について、list2C-5で考えてみます。
xの参照先に注目してみます。

list2C-5

#1からnまでの総和を求める(3を入れた時を想定してコメントを入れます)

def sum_1ton(n):#n = 3を代入してみる
    """1からnまでの整数の総和を求める"""
    s = 0
    while n > 0:#3>0(True)→2>0(true)→1>0(True)→0>0(False)
        s += n#0+3→3+2→5+1→6(終了)
        n -= 1#3-1→2-1→1-1→0(終了)
    return s#3→5→6(終了)

x = int(input('xの値：'))#3を入れる
print(f'1から{x}までの総和は{sum_1ton(x)}です。')#1から3までの総和は6です。

list2C-5の場合、仮引数のnの値が3→2→1…と減っていきます。(最後は0になる)
関数sum_1tonに与えている実引数はxです。実行例の場合関数から戻って来た後に「1から3までの総和は6です」と返ってくるため、変数xの値は3であることが確認できます。この時、仮引数nに実引数xの値がコピーされているのではなく仮引数nに実引数xが代入されているそうです。これは代入でコピーされるものが値ではなく参照先のため、nとxの参照先が同じになるんですね。
つまり、関数実行時にはn, x = 3, 3であるのに対して、関数終了時にはn, x = 0, 3となります。(3自体がイミュータブルなオブジェクトのため、仮引数の参照先が変化します)
次はミュータブルオブジェクトの例です。

list2C-6

#リストの任意の要素の値を更新する(ここではindex, value = 2, 99を想定します)

def change(lst, idx, val):#change([11,22,33,44,55]xを参照, 2, 99)
    """lst[idx]の値をvalに更新"""
    lst[idx] = val #x[2]なので33の位置に99が入り、print関数で出力される
    
x = [11, 22, 33, 44, 55]
print('x =', x)

index = int(input('インデックス：'))#2を入力
value = int(input('新しい値　　：'))#99を入力

change(x, index, value)#change([11,22,33,44,55], 2, 99)
print(f'x = {x}')#変更後のxが参照される([11,22,99,44,55]) 

list2C-5ではxの参照先が3で固定されていたのに対して、list2C-6ではxの参照先が[11,22,33,44,55]から[11,22,99,44,55]に変更されました。
list2C-6の仮引数はlstにあたり、lstとxが同じ参照先になっています。
つまり、lst, x =[11,22,99,44,55], [11,22,99,44,55]で同様の参照先であることがわかりますね。

少しややこしい話な気はしますが、私の解釈ではint型(1などの数字)とlist型(任意で決定するもの)はオブジェクトとして同列に扱われるとなのではないかと思っています。(訂正があればコメントお願いします)

「新・明解Pythonで学ぶアルゴリズムとデータ構造」で勉強日記#8

素数の列挙

素数を列挙するプログラムを考える。
素数は2から始まり、n個まで列挙するのであれば2からn-1までで割り切れないものを見つければ可能です。
最初は効率を無視して仕組みを考えます。

list2-8

#1000以下の素数を列挙(第1版)

counter = 0 #counterの参照を0 (どれくらいの計算量になるか確認するため)

for n in range(2, 1001): #2から1001まででループ
    for i in range(2, n): #2からnまででループ
        counter += 1 #counterに１を追加して参照先を変更
        if n % i == 0: #割り切れると素数ではない
            break #それ以上の繰り返しは不要
    else: #最後まで割り切れなかったら下記を実行(elseはfor文の処理後に行われるもの。今回はbreakがあるためbreakされたらelseは処理されない)
        print(n) #割り切れなかった数字を表示 

print(f'除算を行った回数：{counter}')

2重ループを使っていますね。
気を付けたい点はelseの部分がforに対して並列になっているところでしょうか。
if文の処理は割り切れる数が出た時点で処理を終了して次のループをします。

list2-8では除算の回数が多いため計算回数を減らすプログラムを考えます。

list2-9

#1000以下の素数を列挙(第2版)

counter = 0 #除算の回数
ptr = 0 #得られた素数の個数
prime = [None] * 500 #素数を格納する配列(リストを作成)

prime[ptr] = 2 #2は素数である(リストの0番目に2を格納する)
ptr += 1 #(リストの添字を1増やすイメージ)

for n in range(3, 1001, 2): #対象は奇数のみ(3から1001までの数字を＋2ずつ繰り返す)
    for i in range(1, ptr): #既に得られた素数で割ってみる(1から添字の数だけ繰り返し処理)
        counter += 1
        if n % prime[i] == 0: #
            break
    else:
        prime[ptr] = n #素数として配列に登録
        ptr += 1
        
for i in range(ptr):
    print(prime[i])
print(f'除算を行った回数：{counter}')

更に、改良を考えます

list2-10

#1000以下の素数を列挙

counter = 0 #乗除算の回数
ptr = 0 #得られた素数の個数
prime = [None] * 500 #素数を格納する配列

prime[ptr] = 2 #2は素数である
ptr += 1 #(参照する格納先リストの添字を一つ増やす)
prime[ptr] = 3 #3は素数である
ptr += 1 #(参照する格納先リストの添字を一つ増やす)

for n in range(5, 1001, 2): #対象は奇数のみ
    i = 1 #iは1を参照する
    while prime[i] * prime[i] <= n: #prime[i]×prime[i]以下のnを検討する(Falseの時はelseに行く) 
        counter += 2#prime[i]*prime[i]とn%prime[i]の計算をカウント
        if n % prime[i] == 0: #割り切れると素数ではない
            break#それ以上の繰り返しは不要
        i += 1 #(リスト(prime)の参照する添字を1つ増やす)
    else: #最後まで割り切れなかったら
        prime[ptr] = n#素数として配列に登録
        ptr += 1 ##参照する格納先リストの添字を一つ増やす)
        counter += 1 #(whileの条件部分の計算に対するカウント)

for i in range(ptr): #求めたptr個の素数を表示
    print(prime[i])
print(f'乗除算を行った回数：{counter}')

今回はi×iがn以下の時にループするプログラムになっています。
prime[i]×prime[i]の説明として以下に記述します。

例として100の約数(i×n)で考えると
10×10以降の数字は10×10以前の約数と一致した計算になります。
つまりi×iがn以下の時に割り算をすればよいということになります。
一見するとprime[i]という表記に抵抗出てしまうのですが、一つずつ考えれば納得ですね。

コラム2-7リストの要素とコピー
ここでは、リストについての参照とコピーについて書かれています。
リストの中にリストを作成している場合、階層というものが存在するという話だと思います。

list2C-7

#リストの要素の型が揃う必要がないことを確認
x = [15, 64, 7, 3.14, [32, 55],'ABC']

for i in range(len(x)):
    print(f'x[{i}] = {x[i]}')

#リストはcopyメソッドによってコピーできるがリストを要素として持つリストのコピーはうまく行えない
x = [[1, 2, 3],[4, 5, 6]]
y = x.copy() #コピーのアクセス対象が[1,2,3][4,5,6](list型オブジェクト)になっている
x[0][1] = 9
print(x)
print(y)
#シャロ―コピーが原因でyにも変更が反映される

上記の事態を避けるためには構成要素のレベルでコピーが必要でディープコピーと呼ぶ。copyモジュール内のdeepcopy関数を使用する。

変更版

import copy
x = [[1, 2, 3],[4, 5, 6]]
y = copy.deepcopy(x)#コピーのアクセス対象が1,2,3,4,5,6(int型オブジェクト)になり、リストを形成している
x[0][1] = 9
print(x)
print(y)

参照先の深さをイメージすると理解が進みそう。
シャロ―コピーでは、リストを参照している状態で、yの参照先がxのリストオブジェクト自体を参照先としているため、xを変更したときでもyはxのリストを参照してしまうため変更してしまいます。ディープコピーでは、数(int型でイミュータブルなオブジェクト)自体を参照する状態になっているため、xのリストが変更されてもyの参照先(リスト内の数)が変更することはないと考えればいいですかね。

以上で2章が終了です。ありがとうございました。