1変数の確率微分方程式は一般に次の形で表されます。
$$
dX(t) = f(X(t))dt+g(X(t))dW(t),\ \ X(0)=X_0, 0\leq t \leq T \ \ .
$$
ここで$f,g$はスカラー関数、$W(t)$はウィーナー過程です。この方程式の数値計算をしてみます。
数値計算をするためには、離散化をする必要があります。確率微分方程式の離散化には大きく2つの方法があり、それぞれEuler-Maruyama法とMilstein法と呼ばれています。今回は、精度は劣るものの、簡単であるEuler-Maruyama法を用いて計算します。
まず、区間$[0,T]$を離散化します。じゅうぶん大きな正の整数$N$を用いて、$\Delta t := T/N$、$\tau_j := j \Delta t$とします。また、$X_j:=X(\tau_j)$と表すことにします。
Euler-Maruyama法では次の形式によって方程式を離散化します。
$$
X_j = X_{j-1}+f(X_{j-1})\Delta t + g(X_{j-1}) (W(\tau_j)-W(\tau_{j-1})), j=1,2,\cdots L \ \ .
$$
ここで、$W(t)$はウィーナー過程であることから、$W(\tau_j)-W(\tau_{j-1})$ は平均0、分散 $\tau_j-\tau_{j-1}$ の正規分布 $N(0, \tau_j - \tau_{j-1})$ に従う確率変数です。
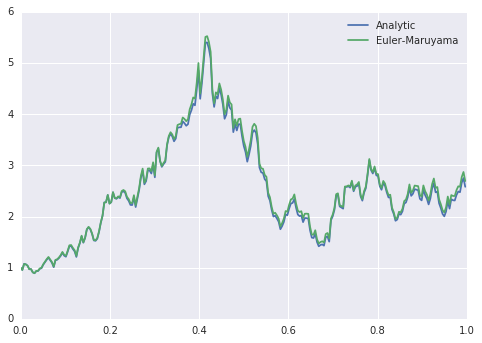
Euler-Maruyama法を使って、下式で表される幾何ブラウン運動を計算してみます。
dX(t) = \sigma X(t) dt + \mu X(t) dW(t), \ \ X(0)=X_0 \ \ .
ここで$\sigma, \mu$は定数です。幾何ブラウン運動は解析解を求めることができ、解は次の通りです。
X(t) = X(0) \exp ( (\sigma-\frac{1}{2}\mu^2)t+\mu W(t) ) \ \ .
Euler-Maruyama法の結果と解析解の結果を比較するコードは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sigma = 2
mu = 1
Xzero = 1
T = 1.0
N = 2**8
dt = T / N
t = np.arange(0.0, T, dt)
dW = np.sqrt(dt) * np.random.randn(N)
dW[0] = 0
W = np.cumsum(dW)
Xtrue = Xzero * np.exp( (sigma - 0.5 * mu**2) * t +(mu*W) )
Xem = np.zeros(N)
Xtemp = Xzero
Xem[0] = Xtemp
for j in range(1, N):
Xtemp = Xtemp + dt * sigma * Xtemp + mu * Xtemp * dW[j]
Xem[j] = Xtemp
plt.plot(t, Xtrue, label='Analytic')
plt.plot(t, Xem, label='Euler-Maruyama')
plt.legend()
