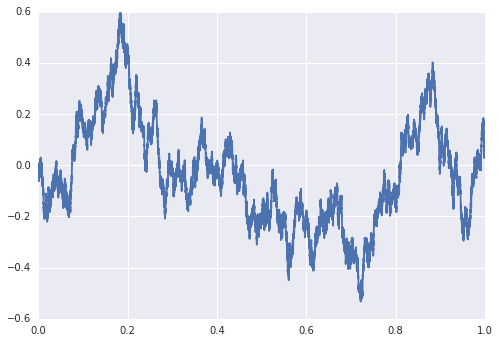
ウィーナー過程 (Wiener Process) $W(t), \ t\in [0,T]$は次の性質を満たします。
- $W(0)=0$
- $0\leq s < t \leq T$である$s,t$において、$W(t)-W(s)\sim N(0, t-s)$である。ただし、$N(\mu,\sigma^2)$は平均$\mu$、 分散$\sigma^2$の正規分布
- $0\leq s < t \leq u < v \leq T$のとき $W(t)-W(s)$と$W(v)-W(u)$は独立
ウィーナー過程の離散化は、正の整数$N$をとり、$\Delta t := T/N$とおき、$t_j := j \Delta t, \ j = 0, \cdots N$、$W_j := W(t_j) $とすれば、
$$
W_j = W_{j-1} + N(0, \Delta t ) \ \ ,
$$
とできます。数値計算では、この差分方程式を計算します。Pythonによるサンプルコードは次の通りです。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
N = 100000
dt = 1.0 / N
t = np.arange(0, 1, dt)
dW = np.sqrt(dt)*np.random.randn(N)
dW[0] = 0
W = np.cumsum(dW)
plt.plot(t, W)