はじめに
以前、wxPythonでオセロをつくろうという記事を書きました。その際、コンピュータのAIとしてまともなものを実装していませんでしたので、少しはちゃんとしたものにしようと思います。
今回導入するのは勉強したてのMin-Max戦略というゲーム戦略です。実装してAI同士で対戦してみたいと思います。
やること
以前の記事で作成したwxPythonのオセロに手を加えます。
- Computer vs Computerのゲームモードを2種類のAIの対戦にする
- 指定した回数 Computer vs Computerの対戦を行い、勝率を表示できるようにする
- 先読み無しのAIを作成する
- 1手先読みするAIを作成する
- Min-Max戦略を行うAIを作成する
すべて実装済みのソースコードはGitHub "alpha-beta"ブランチにありますので、最新版を取得してご覧ください。
前座
Comp vs Compを2種類のAIの対戦にする
comp_aiというスイッチを用意して、ComputerのターンにトグルさせてAIを切り替えています。comp_aiは初期値を[1,-1]をランダムに選択するようにしています。また vs Manの場合はcomp_ai = 0に固定です。
def doComputer(self, my_color):
self.comp_ai *= -1
...
def decideComputerNext(self, pos_list, gain_list):
...
# Insert a computer's AI here
if self.comp_ai >= 0: # comp_ai == 0 => vs Man mode
# Computer AI - A
else:
# Computer AI - B
return next_pos
指定した回数 Comp vs Compの対戦を行い、勝率を表示できるようにする
これはGUIを確認してください。右下に追加しています。
Computer vs Computerを選択し、ループ回数を入れて、「Comp vs Comp Loop」を押すと指定回数だけComp vs Compを行い、各AIの勝利数を表示します。 最下段の数字はAI-A勝利数, AI-B勝利数, Draw の数です。
余談ですが、Windows10でGUIが崩れることに対する対策としてSizerを使用せず、1パネル1コンポーネントでGUIを作成しなおしました。
Sizer使わないとレイアウトが大変です。。。なぜWindows10ではSizerが正しく動かないのか。知ってる方は教えてください。
先読み無しのAIを作成する
先読み無し、つまり石を置ける場所すべてからランダムに置く場所を決めます。
def computerAi_Random(self, pos_list, gain_list):
index = random.randint(0, len(pos_list)-1)
return pos_list[index]
1手先読みするAIを作成する
1手先読み、つまり石を置いたときに取れる相手の石の数が最も多い場所に置きます。
(オセロの定石では、序盤は取れる石が最も少ない位置に置くのが良いらしいのですが。。。まぁ気にしないことにします。)
def computerAi_1stGainMax(self, pos_list, gain_list):
index_list = []
max_gain = max(gain_list)
for i, val in enumerate(gain_list):
if max_gain == val:
index_list.append(i)
tgt = random.randint(0, len(index_list)-1)
return pos_list[index_list[tgt]]
本編
Min-Max戦略(Min-Max法)
Min-Max戦略とは、お互いに最善手を打つとしてゲーム木の状態遷移を進めることを前提として、数手先までのすべての枝を調べる方法です。
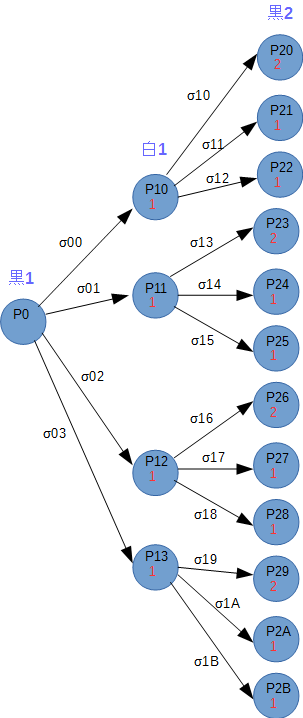
例として黒を自分として最適手を求めてみます。最初の手=黒の手番、3手先まで考えます。
この場合、黒の手番で置ける場所は水色の丸印、ひっくり返せる石の数は丸の中の数です。
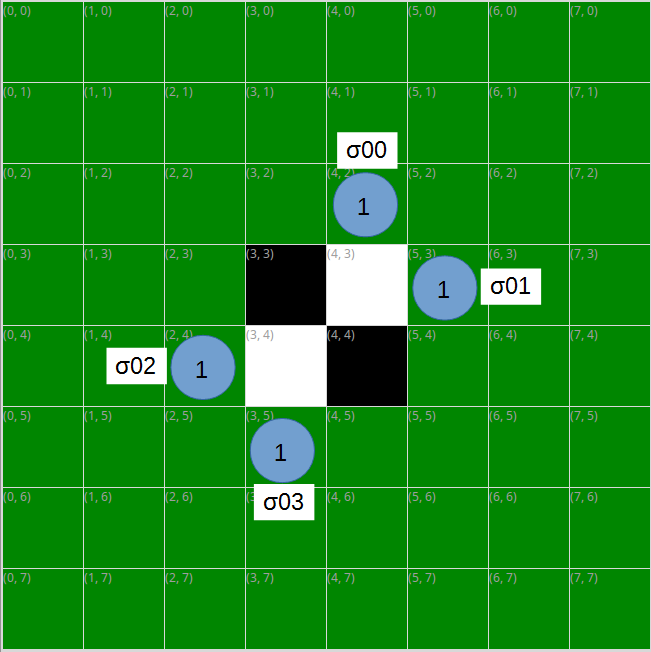
ここで、黒がσ00の手を選んだとすると、次の白の手番で置ける場所と取れる石の数は以下の通りになります。
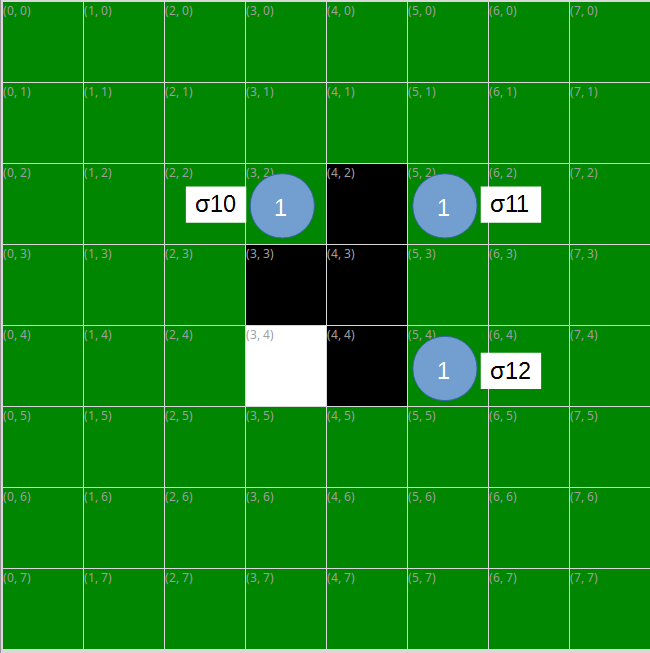
ここで、白がσ10の手を選んだとすると、次の黒の手番で置ける場所と取れる石の数は以下の通りになります。
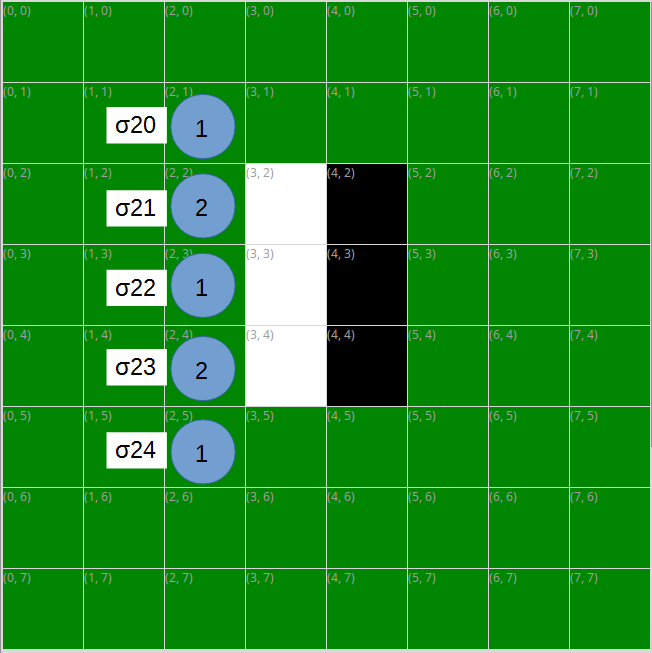
この要領で2手先までのゲーム木を書くと以下のようになります。2手先の黒の手番の評価値は取れる石の数の最大値(σ20~σ24の最大値)です。"黒2"列の丸の中の下段の数字が評価値になります。
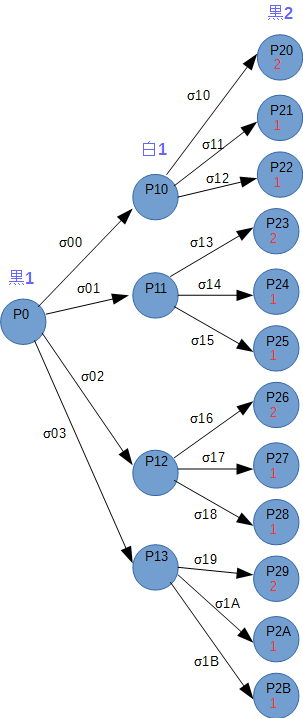
次に1手先の白の手番である"白1"の列に評価値を伝搬させます。白も自身の最善手を選択するので、"黒2"列の評価値が最小になるように手を選ぶはずです。つまり"黒2"の評価値の最小値を"白1"列に伝搬させます。
次に"白1"から"黒1"に評価値を伝搬させます。前回とは逆に黒は自分の評価値が最大になるように手を選ぶはずなので、"白1"の評価値の最大値を伝搬させます。
このように考えていくと、黒の初手が決定できます。
評価値の最小、最大を繰り返して手を決定するので、Min-Max戦略と呼びます。
この例では、σ00 ~ σ03 のどの手でも評価値が変わらないので、どのように置いてもよいことになります。
このことは初手で置ける場所が点対称になることからも直感的に正しそうです。
ちょっと面白味にかける例でしたね。ゲーム後半で考えると、木の大きさが非常に大きくなるので、初手を例にさせていただきました。
実装
実装してみます。
3手先読みなのに、minMaxのmax_depthがなぜ2なのかというと、computeAi_MinMax_3の中で最後の評価値伝搬を行っているので、引数には1引いた数を入れます。
def computerAi_MinMax_3(self, pos_list, gain_list):
value = []
update_pos_list = []
self.log_on = False
value = self.minMax(2, 2, pos_list, gain_list)
for i, pos in enumerate(pos_list):
if max(value) == value[i]:
update_pos_list.append(pos)
self.log_on = True
tgt = random.randint(0, len(update_pos_list)-1)
return update_pos_list[tgt]
def minMax(self, depth, max_depth, pos_list, gain_list): # depth > 0
value = []
next_value = []
next_pos_list = []
next_gain_list = []
self.backUpAllState(self.state_storage_list[depth])
for pos in pos_list:
ret = self.putComputerStone(pos, False)
next_pos_list, next_gain_list = self.scanPuttableCell()
if (depth > 1):
next_value = self.minMax(depth-1, max_depth, next_pos_list, next_gain_list)
if len(next_value) == 0:
value.append(0)
elif (max_depth - depth) % 2 == 0:
value.append(min(next_value))
else:
value.append(max(next_value))
else:
if len(next_gain_list) == 0:
value.append(0)
elif (max_depth - depth) % 2 == 0:
value.append(min(next_gain_list))
else:
value.append(max(next_gain_list))
self.restoreAllState(self.state_storage_list[depth])
return value
ちょっと冗長な部分が残りましたが、すっきりと実装できました。ただここまで来るのにとても時間がかかりましたが。。。
AI同士対戦
AI同士で100戦対戦してみます。先攻、後攻はランダムに設定されています。
- Min-Max_3手先読み vs 先読み無し
- Min-Max_3手先読み vs 1手先読み
結果は以下のようになりました。
- Min-Max 70勝、25敗 5引き分け
- Min-Max 48勝、48敗、4引き分け
おや、Min-Max戦略あまり強くないですね。実装は合っていると思うのですが。
まあ、先読み無しに勝ち越しているのが救いでしょうか。
ちなみに、このMin-Max戦略は非常に時間がかかります。ご自身の手でComputer vs Computerの対戦をさせる場合には、PCの性能にもよりますが、100戦するのに10分くらいかかりますのでご注意ください。
今後はMin-Max戦略の探索範囲を狭くすることで高速化を図るαβ戦略の実装も試そうと思います。
あとづけ
Min-Max戦略が上手くいかなかった理由として考えられるのは、どこの石でも+1として値を評価していたことです。
そこで各場所に重みをつけます。角がなんとなく評価値が高そうなのは分かりますが、ちょっと手づまりだったので、こちらのサイトを参考にさせていただきました。
http://uguisu.skr.jp/othello/5-1.html
というわけで以下のように重みづけをして、gainを得られるように改造します。

gGain = [( 30, -12, 0, -1, -1, 0, -12, 30), \
(-12, -15, -3, -3, -3, -3, -15, -12), \
( 0, -3, 0, -1, -1, 0, -3, 0), \
( -1, -3, -1, -1, -1, -1, -3, -1), \
( -1, -3, -1, -1, -1, -1, -3, -1), \
( 0, -3, 0, -1, -1, 0, -3, 0), \
(-12, -15, -3, -3, -3, -3, -15, -12), \
( 30, -12, 0, -1, -1, 0, -12, 30)]
...
def vecScan(self, pos, reverse_on):
rev_list = []
temp_list = []
gain = 0
is_hit = 0
if reverse_on == 0 and self.getCellState(pos,(0,0)) != "green":
return 0, gain
if self.now_color == "black":
rev_color = "white"
else:
rev_color = "black"
for v in gVec:
temp_list = []
for i in range(1, 8):
if self.getCellState(pos,(v[0]*i,v[1]*i)) == rev_color:
temp_list.append(self.movePos(pos,(v[0]*i, v[1]*i)))
if self.getCellState(pos,(v[0]*i+v[0], v[1]*i+v[1])) == self.now_color:
is_hit = 1
for j in temp_list:
rev_list.append(j)
break
else:
break
if reverse_on == True:
if self.log_on == True:
self.log_textctrl.AppendText("put:" + str(pos) + ", " + str(rev_list) + " to " + str(self.now_color) + "\n")
for rev_pos in rev_list:
self.setCellState(rev_pos, (0,0), self.now_color)
if self.now_color == "black":
self.player_score[0] += 1
self.player_score[1] -= 1
else:
self.player_score[1] += 1
self.player_score[0] -= 1
self.updateScoreLabel()
gain = self.calcGain(pos, rev_list)
return is_hit, gain
def calcGain(self, pos, rev_list):
ret_gain = 0
ret_gain += gGain[pos[0]][pos[1]]
for rev_pos in rev_list:
ret_gain += gGain[rev_pos[0]][rev_pos[1]]
return ret_gain
それでは改めて対戦させてみます。
- Min-Max_3手先読み vs 先読み無し
- Min-Max_3手先読み vs 1手先読み
- 1手先読み vs 先読み無し
結果は以下のようになりました。
- Min-Max 38勝、55敗、7引き分け
- Min-Max 19勝、80敗、1引き分け
- 1手先読み 83勝、16敗、1引き分け
うぅ... Min-Maxの勝率が下がってしまいました。
1手先読みがかなり強いです。
再考の余地ありです。お粗末様でした。