fix関数についての解説記事が少なかったので、頑張ってかき集めた情報をまとめておこうと思います。
内容としては、
- fix関数 <- 今ココ
- MonadFixと再帰的do記法
- ArrowLoopと再帰的arrow記法
を複数の記事に分けて紹介します。
-
fix関数なら大体知っているよっていう人は、説明を飛ばして、後ろの練習問題から始めても楽しいと思います。
-
fix関数の仕組みはいいから、使い方だけ教えて~~っていう人は、fix関数の活用法から始めると幸せかもしれません。
この記事に載せているソースコードは、モジュールのimport文を省いています。なので、実際に手元の環境で動かしてみるときは、次のimport文をソースコードの冒頭に追加して実行してください。
import Control.Monad.Fix -- fix関数をインポート
import Control.Monad.State -- Stateモナドをインポート
import Text.Read -- readMaybe関数をインポート
前提知識
Haskellの基本的な使い方は説明しません_(._.)_
- 変数や関数の定義方法
- 関数のカリー化と部分適用
- 基本的な関数たち(
id、const、takeとか)
は知っておいた方が読み易いと思います。
Haskellerの登竜門といわれるモナドについては、知らなくても大きな問題はありません。ただ、練習問題2ではStateモナドを使っているので、そこだけはモナドの知識が必要です。
それでは、準備はよろしいですか?
fix関数
fix :: (a -> a) -> a
fix f = let x = f x in x
定義から分かる通り、fix関数は関数を引数に取る高階関数です。
とりあえず、適当な関数を放り込んでみましょう。恒等関数idを引数として渡してみます。
fix id
。。。(-_-)zzz
いつまで経っても処理が終わりませんね。ご察しの通り、無限ループになってしまいました。
ループの中で、Haskell処理系がどんな処理をしているのか覗いてみましょう。
fix id
-- fixを関数適用
= let x = id x in x
-- 変数xを展開
= id x
-- idを関数適用
= x
-- 変数xを展開
= id x
-- idを関数適用
= x
-- 変数xを展開
= id x
...
なるほど、いつまで経っても処理が終わらないわけです。
次に、定値関数const 0を引数として渡してみましょう。
fix (const 0)
-- 0
今度は値が求まりましたね。
さっきと同じように、Haskell処理系の動きを覗いてみましょう。
fix (const 0)
-- fixを関数適用
= let x = const 0 x in x
-- 変数xを展開
= const 0 x
-- constを関数適用
= 0
確かに、答えは0になりました。
今回とさっきは何が違うかったかというと、関数fの値を決めるために引数xの値が必要1かどうかが違いました。
恒等関数idの場合は、
id x = x
だったので、関数idの値を決めるために引数xの値が必要でした。
一方、定値関数const 0の場合は、
const 0 x = 0
だったので、関数const 0の値を決めるために引数xの値は必要ではありません。
一般に、関数fの値が引数xの値によらず決まるとき、そしてその時に限り、fix関数は無事に終了してその値を返します。
不動点
ここでは、fix関数が返す値の意味を考えます。
fix関数は、
fix :: (a -> a) -> a
fix f = let x = f x in x
と定義されていたので、fix fの返り値をaとすると、
a = f a
が成り立ちます。つまり、値aは関数fに通しても、そのまま出てきます。
このような値のことを、関数fの不動点といいます。
関数の不動点は一つとは限りません。例えば、恒等関数idでは、あらゆる値が不動点となります。
それでは、fix関数が返す不動点はどのように選ばれるのでしょうか。答えは、その関数の"最も定義されていない"(least-defined)不動点を返します。最も定義されていないとはどういうことなのかは、難しいので説明しません(=できません)。詳しくは、Denotational semantics - Wikiを参照してください_(._.)_
数多ある値の中で、最も定義されていない値はボトム⊥です。ボトム⊥として、Haskellではundefinedが実装されています。また、計算が終わらず無限ループする場合もボトム⊥が返されたと考えます。
つまり、fix関数は、関数fがボトム⊥を不動点としてもつ場合は、必ずボトム⊥を返します(=計算が終わらないorエラーが出る)。実はこれは、
関数fの値が引数xの値によらず決まるとき、そしてその時に限り、fix関数は無事に終了してその値を返します
の言い換えになっています。
fix関数が終了しない場合
fix関数が終了しなくてもよい場合があります。
例えば、fix関数を使って無限リストを作る場合などです。ここでは、1が無限に続くリストをfix関数で作ってみます。
ls = fix $ \x -> 1:x -- (*)
実際に先頭の10要素を取ってくると、
take 10 ls
-- [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
となっています。
ちょっと待ってください!!
(*)式の右辺を展開してみると、
fix $ \x -> 1:x
= let x = (\x -> 1:x) x in x
= (\x -> 1:x) x
= 1:x
= 1:((\x -> 1:x) x)
= 1:(1:x)
= 1:1:x
...
となって、計算は終了しないはずです。しかし、(*)式は終了します。
???
これは、Haskellが計算結果を遅延評価するためです。つまり、必要になるまで(*)の右辺は計算されずにほったらかしにされます。この状態のことをサンクといいます。
サンクは必要になったら必要な分だけ評価されます(=計算が進められます)。
例えば、(*)式の右辺のサンクは、take 5 lsによって、
ls = 1:1:1:1:1:x
まで計算が進められます。
この仕組みによって、fix関数は、たとえ終了しなくても意味のある結果を返すことが出来るようになっています。
fix関数を使った設計法
この章はMonadFix is Time Travelを下敷きとして書いています。詳しくは、ネタ元の記事をご覧ください。
ここまではfix関数の性質を紹介してきましたが、この章ではじゃあ実際にどうやってfix関数を使ったプログラムを組むのかを紹介します。
fix関数の定義をもう一度見返してみましょう。
fix f = let x = f x
関数fに自身の返り値xが引数として渡されていますね。ということは、関数fは実行前に自身の実行結果を知ることができると考えることができます。そして、実行結果をもとにして関数を実行することができます。なんと、未来のことが分かるんです!!
この考えのもとで、次のfibonacci数列を生成するプログラムを見ていきましょう。
fix $ \fibs -> 1 : 1 : zipWith (+) fibs (tail fibs)
ここでは、fix関数に渡す関数f = \fibs -> 1 : 1 : zipWith (+) fibs (tail fibs)は、
f fibs = 1 : 1 : zipWith (+) fibs (tail fibs)
と定義されているとみなせます。
実行結果のリストfibsと、そのリストを一つずらしたリストtail fibsを足し合わせたリストを、第3項以降につなぎ合わせています。数列として書き直すと、
[a_1 = 1,\ a_2 = 1,\ a_3 ... = [a_1,\ a_2,\ ...] + [a_2,\ a_3,\ ...]]
となっています。整理すると確かに、
[a_1,\ a_2,\ a_3 = a_1 + a_2,\ a_4 = a_2 + a_3,\ ...\ ,\ a_n = a_{n-2} + a_{n-1}]
となっていますね。
fix関数の活用法
ここからは、fix関数が現実のプログラムでどのように使われるのか、実例を紹介していきます。
活用法1:無限リスト
fix関数を使うと無限リストが簡単に作れます。
ls = fix $ \xs -> [1:2:xs]
-- take 5 ls
-- [1, 2, 1, 2, 1]
この例だけでは、cycle関数(Haskellの無限リスト系関数 - Qiitaを参照)を使えばいいじゃないかというマサカリが飛んできそうなので、もう少し複雑な例も挙げておきます。
ls = fix $ \fibs -> 1 : 1 : zipWith (+) fibs (tail fibs)
-- take 5 ls
-- [1, 1, 2, 3, 5]
(What does fixIO do? - StackOverflowより引用)
皆さんご存じのfibonacci数列です。こんな手の込んだ無限リストもfix関数を使えば作れます。
活用法2:forループ
Haskellのループ処理は flip fix でだいたい書けそう - Qiitaに詳しく書かれていますが、fix関数を使うと他言語でいうforループを実装できます。
例えば、階乗を求める関数factは、Pythonではfor文をつかって、
def fact(n):
r = 1
for i in range(n):
r *= (i + 1)
return r
# fact(5)
# 120
と書けます。
これをHaskellでは、
fact n = (flip fix) n p where
p _ 1 = 1
p f i = i * f (i - 1)
-- fact 5
-- 120
と書くことができます。
活用法3:再帰関数の書き直し(ちょいムズ)
あらゆる再帰関数は、fix関数を使って"見かけ上"2再帰形でない形に書き直すことができます。
ちょっと抽象的で分かりづらいですが、あらゆる再帰関数fは適切な高階関数gを使って、
f = g (f) -- (*)
と書き表すことができます。
これをfix関数を使って書き直すと、
f = fix g
となります。fix関数を使うと右辺から関数fを消去できるので、関数fは見かけ上再帰形ではなくなります。
この説明だけだと、何のこっちゃ??となっていると思いますので、具体例としてfibonacci数を求める関数を考えてみます。
まずは、再帰関数で書いてみます。
fib n = if n <= 1 then n else fib (n - 1) + fib (n - 2)
次に、右辺をfibを引数にとる高階関数で書き直します。
fib n = g (fib) n where
g f = \x -> if x <= 1 then x else f (x - 1) + f (x - 2)
さらに、関数fibの引数nを消去して、ポイントフリースタイルに書き直します。
fib = g (fib) where
g f = \x -> if x <= 1 then x else f (x - 1) + f (x - 2)
(*)の形になりました。
最後に、fix関数を使って関数fibを書き直します。
fib = fix g where
g f = \x -> if x <= 1 then x else f (x - 1) + f (x - 2)
あるいは、高階関数gを少し直して、
fib = fix g where
g f x = if x <= 1 then x else f (x - 1) + f (x - 2)
となります。
ところで、あらゆるループは再帰関数に書き直せる3のでした。そして、あらゆる再帰関数はfix関数で書き直せるということは、、、
あらゆるループはfix関数で書き直すことができます!!
詳しくは、不動点コンビネータで検索してね。
活用法4:無限ループ
fixを使うと無限ループを簡単に作ることができます(怖い!!)。通常の処理では無限ループは避けるべきものですが、例えばインタープリタなどのREPLプログラムでは、ユーザーの入力を受け付け続ける必要があるので、main関数を無限ループにする必要があります。そういう時は、main関数をfix関数を使って定義することができます。
例として、ユーザーに数字を入力してもらい、その数字の偶奇判定をするプログラムを書いてみます。なお、ユーザーが数字以外を入力した場合には停止します。
まずは、ループなし版を示します。ユーザー入力後に偶奇判定をして、そのまま終了するプログラムです。
main = do
p <- readMaybe <$> getLine
case p of
Just x | x `rem` 2 == 0 -> print "Even"
| otherwise -> print "Odd"
Nothing -> print "Quit"
-- < 123
-- > Odd
次に、fix関数を使ってループさせます。
main = fix $ \m -> do
p <- readMaybe <$> getLine
case p of
Just x | x `rem` 2 == 0 -> print "Even" >> m
| otherwise -> print "Odd" >> m
Nothing -> print "Quit"
-- < 123
-- > Odd
-- < 122
-- > Even
-- < abc
-- > Quit
活用法5:メモ化
メモ化については、再帰関数とメモ化とフィボナッチ数列を参考にしてください。参考記事ではpythonを使っていますが、メモ化の実装についてはHaskellでの実装よりも分かりやすいので、この章のプログラムと見比べてみると理解が進むと思います。
Haskellの関数は参照透明性があるため、メモ化との相性がとても良いです。一方で、リストの改変や変数の再代入が許されないため、計算結果をどうやってメモするのかは悩みどころとなります。その方法の一つがfix関数を使うやり方です。
fix関数を使ったfibonacci数列の求め方(再掲) <- めっちゃ速い!!
sequence = fix $ \fibs -> 1 : 1 : zipWith (+) fibs (tail fibs)
-- take 5 sequence
-- [1, 1, 2, 3, 5]
(What does fixIO do? - StackOverflowより引用)
特定のfibonacci数を求める方法は他にも、
fib :: (Int -> Integer) -> Int -> Integer
fib f 0 = 1
fib f 1 = 1
fib f n = f (n - 1) + f (n - 2)
memoize :: (Int -> a) -> (Int -> a)
memoize f = (map f [0 ..] !!)
fibMemo :: Int -> Integer
fibMemo = fix (memoize . fib)
-- fibMemo 4
-- 5
(Memorization - Wikiより引用)
両方とも、途中計算をリストにメモすることで計算量をO(N)に抑えているため、高速に処理できています。
途中計算をリストにメモできるのは、Haskellが遅延評価で動く言語であり、さらにグラフ簡約という方法でプログラムを実行しているからです。詳しくは、遅延評価の仕組みやGraph Reduction (Reduction + Sharing) - Wikiを参照してください。
練習問題
1. fibonacci数列改(難易度★)
通常のfibonacci数列の漸化式は、
a_{n+2} = a_{n} + a_{n+1}
で、fibonacci数列を求めるプログラムはfix関数を使って、
fix $ \xs -> 1:1:zipWith xs (tail xs)
と書けるのでした。
この数列を改造し、漸化式が、
a_{n+3} = a_{n} + a_{n+1} + a_{n+2}
となる数列を求めるプログラムをfix関数を使って書いてみてください。
解答例
zipWith関数を3つのリストに適用すればよさそうですね。
fix $ \xs -> 1:1:1:foldr (zipWith (+)) (repeat 0) [xs, tail xs, (tail . tail) xs]
-- take 10 ls
-- [1,1,1,3,5,9,17,31,57,105]
他にも、ParallelListComp言語拡張を使うとすっきりと書けます。
{-# LANGUAGE ParallelListComp #-}
fix $ \xs -> 1:1:1:[a + b + c | a <- xs | b <- tail xs | c <- (tail . tail) xs]
2. ハノイの塔(難易度★)
再帰関数で解く問題で最も有名なのはハノイの塔だと思います。
fix関数の活用法3で紹介した、fix関数を使った再帰関数の書き換え方を応用して、ハノイの塔の円盤の動きをシミュレートするプログラムをfix関数で書いてください。
ちなみに再帰関数を使うと、
type Tower = [[Int]]
-- 円盤を1枚iからjに移動
move :: Int -> Int -> State Tower ()
move i j = do
tw <- get
let k = 3 - i - j
ti = tw !! i
tj = tw !! j
tk = tw !! k
let (ti', tj') = go (ti, tj)
put $ build (i, ti') (j, tj') (k, tk)
where
go ([], ys) = ([], ys)
go (x:xs, ys) = (xs, x:ys)
key (i, _) (j, _) = compare i j
build xp yp zp = map snd $ sortBy key [xp, yp, zp]
-- 円盤をn枚iからjに移動
trans :: Int -> Int -> Int -> State Tower ()
trans i j 1 = move i j
trans i j n = do
let k = 3 - i - j
trans i k (n - 1)
trans i j 1
trans k j (n - 1)
solve n = execState (trans 0 2 n) tw
where tw = [[1..n], [], []]
-- solve 5
-- [[], [], [1, 2, 3, 4, 5]]
と書けます。
解答例
再帰形になっているのは関数transの部分なので、そこをfix関数で書き直せばよいですね。
今回は引数の数が3つに増えているので、その点に注意して書き直しましょう。
type Tower = [[Int]]
-- 円盤を1枚iからjに移動(そのまま)
move :: Int -> Int -> State Tower ()
move i j = do
tw <- get
let k = 3 - i - j
ti = tw !! i
tj = tw !! j
tk = tw !! k
let (ti', tj') = go (ti, tj)
put $ build (i, ti') (j, tj') (k, tk)
where
go ([], ys) = ([], ys)
go (x:xs, ys) = (xs, x:ys)
key (i, _) (j, _) = compare i j
build xp yp zp = map snd $ sortBy key [xp, yp, zp]
-- 円盤をn枚iからjに移動(fixで書き直し)
trans' :: Int -> Int -> Int -> State Tower ()
trans' = fix g where
g f i j 1 = move i j
g f i j n = do
let k = 3 - i - j
f i k (n - 1)
f i j 1
f k j (n - 1)
solve n = execState (trans' 0 2 n) tw
where tw = [[1..n], [], []]
-- solve 5
-- [[], [], [1, 2, 3, 4, 5]]
3. 動的計画法(難易度★★)
fix関数の活用法5では、fix関数を使ってメモ化ができると紹介しました。
メモ化が有効に活用できる分野は非常に多いですが、その中でも動的計画法(DP)ではメモ化が中心的な役割を果たしています。
次の問題を動的計画法で解くプログラムを書いてみてください。なお、メモ化を忘れずに!!
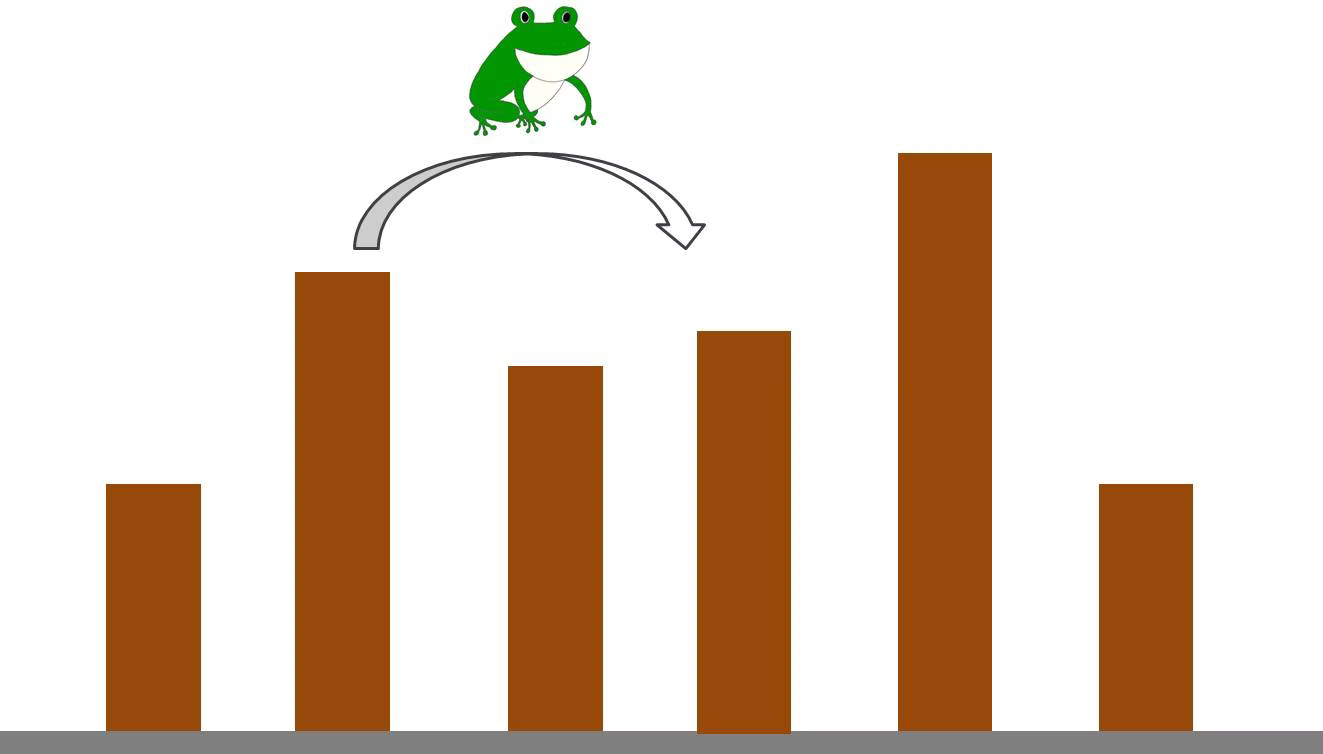
N 個の足場があって、i 番目の足場の高さは hi です。
最初、足場 1 にカエルがいて、ぴょんぴょん跳ねながら足場 N へと向かいます。カエルは足場 i にいるときに
足場 i から足場 i+1 へと移動する (そのコストは |hi−hi+1|)
足場 i から足場 i+2 へと移動する (そのコストは |hi−hi+2|)
のいずれかの行動を選べます。カエルが足場 1 から足場 N へと移動するのに必要な最小コストを求めよ。
(動的計画法超入門! Educational DP Contest の A ~ E 問題の解説と類題集より引用)
ヒントとして、テストケースとPythonでの解答例を載せておきます。
| N | hs | 最小コスト |
|---|---|---|
| 4 | 10, 30, 40, 20 | 30 |
| 2 | 10, 10 | 0 |
| 6 | 30, 10, 60, 10, 60, 50 | 40 |
| 7 | 2,9,4,5,1,6,10 | 8 |
inf = 1000000 # すごく大きな数
def solve(N, hs):
dp = [0] * N
def cost(i, j):
if i < 0:
return inf
else:
return dp[i] + abs(hs[j] - hs[i])
for i in range(1, N):
dp[i] = min (cost(i - 2, i), cost(i - 1, i))
return dp[N - 1]
解答例
メモの型は[(Int, Int)]で、その意味は[(i, 足場iまでの最小コスト)]としました。
足場の高さのリストhsにアクセスするために、足場の番号もメモに含める必要があります。
-- 足場iから足場jへと移動するときのコスト
cost :: [Int] -> Int -> Int -> Int
cost hs i j = abs (hi - hj) where
hi = hs !! i
hj = hs !! j
-- 足場iまでの最小コストと足場j(=i+1)までの最小コストから、
-- 足場k(=i+2)までの最小コストを計算
calc :: [Int] -> (Int, Int) -> (Int, Int) -> (Int, Int)
calc hs (i, wi) (j, wj) | i + 1 == j =
let k = j + 1
ci = wi + cost hs i k
cj = wj + cost hs j k
in (k, min ci cj)
-- 足場nまでの最小コストを動的計画法で計算
solve :: Int -> [Int] -> Int
solve n hs = snd $ (!! (n - 1)) $ fix g where
g ws = (0, 0):(1, cost hs 1 0):zipWith (calc hs) ws (tail ws)
-- solve 7 [2, 9, 4, 5, 1, 6, 10]
-- 8
足場の番号をメモに含めたくない場合は、zipWith関数ではなくmap関数を使い、メモのベースとなるリストから足場の番号を取得するとよいです。
inf :: Int
inf = 100000 -- すごく大きな数
-- 足場iから足場jへと移動するときの足場jでの最小コストを計算
cost :: [Int] -> [Int] -> Int -> Int -> Int
cost hs ws i j
| i < 0 = inf
| otherwise = wi + abs (hi - hj) where
wi = ws !! i
hi = hs !! i
hj = hs !! j
-- 足場(n-2)までの最小コストと足場(n-1)までの最小コストから、
-- 足場nまでの最小コストを計算
calc :: [Int] -> Int -> [Int] -> Int
calc hs n ws =
let ci = cost hs ws (n - 1) n
cj = cost hs ws (n - 2) n
in min ci cj
-- 足場nまでの最小コストを計算
solve :: Int -> [Int] -> Int
solve n hs = (!! (n - 1)) $ fix $ \ws ->
let f 0 = 0 -- 足場の番号が0のとき
f i = calc hs i ws -- 足場の番号がiのとき
in map f [0..] -- 足場の番号のリスト
-- solve 7 [2, 9, 4, 5, 1, 6, 10]
-- 8
参考文献
fix関数
- 不動点と再帰 - Wiki
- Haskellのループ処理は flip fix でだいたい書けそう - Qiita
- MonadFix is Time Travel
- Fix and recursion - Wiki
- おとうさんにもわかるYコンビネータ!(絵解き解説編)
- 不動点とfix演算子
- 不動点コンビネータ - Wikipedia
遅延評価
- 正格性のすべて (翻訳)
- 正格評価と遅延評価(詳細編)
- 遅延評価の仕組み
- Graph reduction - Wiki
- サンクの構造を見る
- 反駁不可パターン
- Strict拡張を使用する際の注意点
- Weak head normal form - Wiki
- Thunk - Wikipedia
ソースコード
-
関数
fの値を決めるために、引数xの値が必要なことを、関数fは引数xについて正格であると言います。詳しくは、fixと不動点 - Wikiを参照してください。 ↩ -
fix関数が再帰形で定義されているので、実質的には再帰関数のままです。つまり、再帰関数を使うときに起こる、スペースリークや関数呼び出しのオーバーヘッドといった問題は、fix関数で書き直すことでは解消されません。 ↩
-
ループを再帰関数にする考え方に実例が載っています。 ↩