Vision Transformerの実装から学ぶPytochの処理実装練習~Attention編~

はじめに

論文やその解説記事を読んでdeep learnigのアーキテクチャに関しての概要は理解できたけど、その実装コードは読んでも複雑でよくわからないという場面も多いかと思われます。
そこで、論文の実装コードを題材としてpytorchの実装力を磨くための問題をまとめることが本記事の目的としています。

題材

今回は画像認識で有名な「Vision Transformer」に注目してその中でもAttention処理を行うクラスの実装を題材に紹介していきたいと思います。
また、今回は実装コードの紹介がメインとなるためAttentionについて詳細な説明は割愛します。
以下に、参考文献を紹介するので必要に応じてそちらも参照ください。

参考文献

• https://github.com/lucidrains/vit-pytorch ←　本記事での実装において参考としたリポジトリ
• https://developers.agirobots.com/jp/multi-head-attention/ ←　Attentionに関するわかりやすい解説記事
• https://arxiv.org/abs/2010.11929 ←　元論文

本編

実装する処理の概要

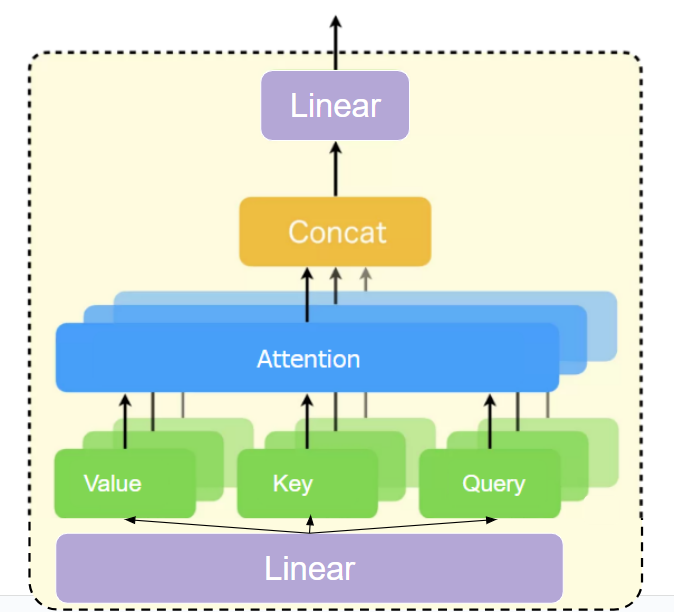
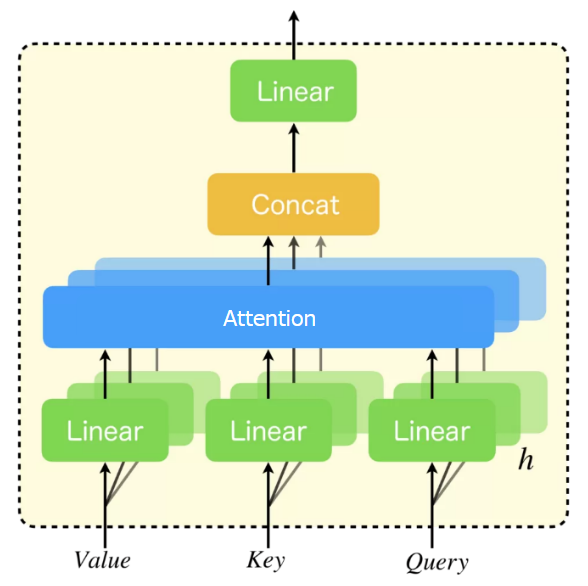
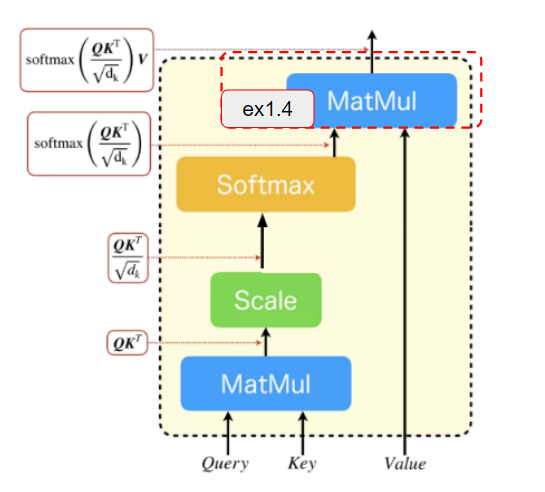
以下がこれから実装するMULTIHEAD SELF-ATTENTION処理の概要になります。

(図はこちらの記事から引用したものに少し編集を加えたものです。)

ex1 attentionの計算

最初にAttentionの計算処理の実装から始めていきます。
AttentionはVision Transformerの論文中で以下のように数式などを用いて説明されています。

これの処理の流れを図にすると以下のように描くことができます。

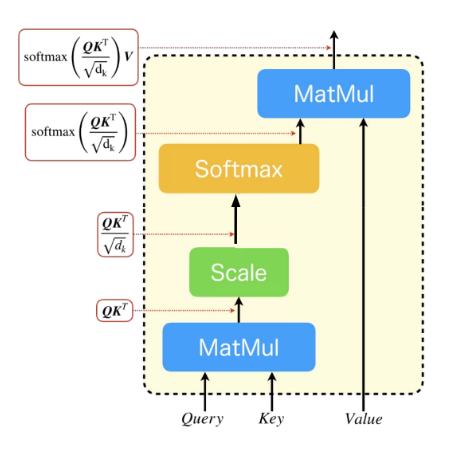
ここで、$\boldsymbol{Q}$、$\boldsymbol{K}$、$\boldsymbol{V}$はそれぞれQuery、Key、Valueのテンソルを$d_{k}$は$\boldsymbol{Q}$($\boldsymbol{K}$、$\boldsymbol{V}$も同じサイズ)の末尾の次元のサイズです。

(図はこちらの記事から引用したものに少し編集を加えたものです。)
まずは簡単のためにバッチ、headが存在しない場合である[n,$d_{k}$]サイズの２次元テンソルを入力として想定した場合での実装をしていきます。この場合、Attentionで行われる処理はすべて高校3年～大学１年で履修する行列の計算となります。ここでは、コードの実装と合わせて以下のインプットデータを例にコードの処理を手計算で確認していきたいと思います。
$$
\boldsymbol{Q}=
\begin{pmatrix}
1 & 2 \\
3 & 4 \
\end{pmatrix},
\boldsymbol{K}=
\begin{pmatrix}
5 & 6 \\
7 & 8 \
\end{pmatrix},
\boldsymbol{V}=
\begin{pmatrix}
9 & 10 \\
11 & 12 \
\end{pmatrix}
$$

import torch
import torch.nn as nn
from einops import rearrange, repeat

# tensor shape: [n,d_k] = [2,2]
# まずは、簡単のためBとHは無視する
Q = torch.tensor([[1.0,2.0],[3.0,4.0]]) 
K = torch.tensor([[5.0,6.0],[7.0,8.0]]) 
V = torch.tensor([[9.0,10.0],[11.0,12.0]])

ex1.1

最初の問題は、$\boldsymbol{Q}\boldsymbol{K}^T$の計算をコードで実装することです。

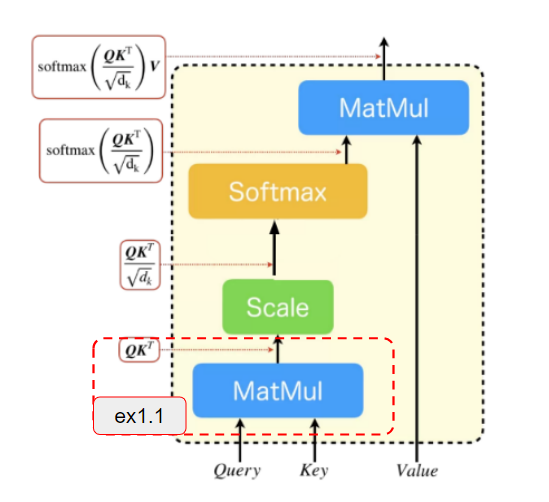
テンソルの計算はtorch.matmulというPytorchの提供するテンソル積計算のメソッドがあるためそちらを活用してみてください。

# 問題
# 以下の変数ex1_1に計算結果を代入してみてください。
ex1_1 = 

さっそく回答を紹介します。

# 回答
ex1_1 = torch.matmul(q, k.transpose(-1, -2))
print(ex1_1)

次の問題に行く前に手計算で確かめてみましょう。
$$
\begin{align}
\boldsymbol{Q}\boldsymbol{K}^T &=
\begin{pmatrix}
1 & 2 \\
3 & 4 \
\end{pmatrix}
\begin{pmatrix}
5 & 7 \\
6 & 8 \
\end{pmatrix} \\
&= \begin{pmatrix}
1×5+2×6 & 1×7+2×8 \\
3×5+4×6 & 3×7+4×8 \
\end{pmatrix} \\
&= \begin{pmatrix}
17 & 23 \\
39 & 53 \
\end{pmatrix}
\end{align}
$$
手計算の結果と一致することが確認できました。

ex1.2

次にex1.1の結果にスケール処理を適用します。

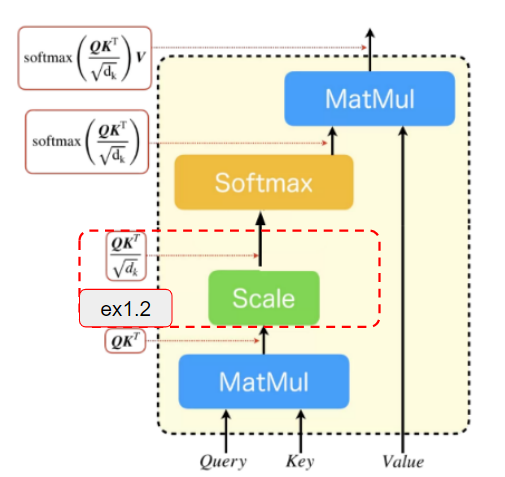
先のex1.1の出力結果が[n,$d_{k}$]=[2,2]のサイズのテンソルであることから$d_k=\sqrt{2}$でex1.1の結果を割ればよいとわかります。

# 問題
# 以下の変数ex1_2に計算結果を代入してみてください。
ex1_2 = 

さっそく回答を紹介します。

# 回答
scale = 2**-0.5
ex1_2 = ex1_1 * scale
print(ex1_2)

ここでも、検算してみましょう。手計算だと大変なため関数電卓などを使用して確かめてみたください。
$$
\begin{align}
\frac{\boldsymbol{Q}\boldsymbol{K}^T}{\sqrt{d_k}} &=
\begin{pmatrix}
17 / \sqrt{2} & 23 / \sqrt{2} \\
39 / \sqrt{2} & 53 / \sqrt{2} \
\end{pmatrix}\\
&= \begin{pmatrix}
12.02... & 16.26... \\
27.57... & 37.47... \
\end{pmatrix}
\end{align}
$$

ex1.3

次にex1.2の結果にsoftmax処理を適用します。

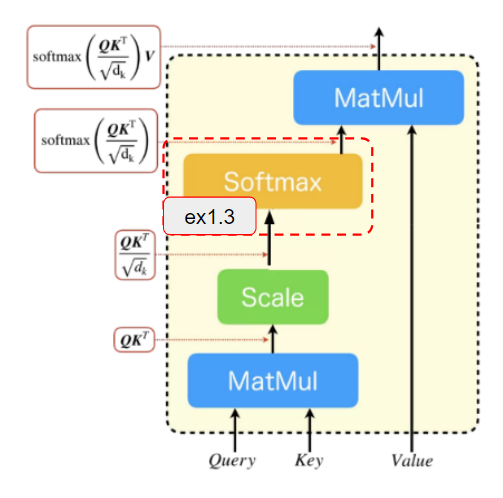
softmax処理はPytorchの提供しているsoftmaxメソッドがあるためそちらを活用して見てください。

# 問題
# 以下の変数ex1_3に計算結果を代入してみてください。
softmax = 
ex1_3 = softmax(ex1_2)

さっそく回答を紹介します。

# 回答
softmax = nn.Softmax(dim=-1)
ex1_3 = softmax(ex1_2)

次に検算をしていきます。注意する点としてはここではsoftmax関数を行列の行方向に対して適用しているという点です。

実際に計算してみると（こちらも関数電卓などでの計算を推奨）
$$
\begin{align}
\text{softmax}\left(\frac{\boldsymbol{Q}\boldsymbol{K}^T}{\sqrt{d_k}}\right)
&= \begin{pmatrix}
\frac{exp(12.02)}{exp(12.02)+exp(16.26)} & \frac{exp(16.26)}{exp(12.02)+exp(16.26)} \\
\frac{exp(27.57)}{exp(27.57)+exp(37.47)} & \frac{exp(37.47)}{exp(27.57)+exp(37.47)} \
\end{pmatrix} \\
&= \begin{pmatrix}
0.014... & 0.98... \\
0.000050... & 0.99994... \
\end{pmatrix}
\end{align}
$$
となります。検算の結果とコード実行の結果が微妙にずれるかもしれませんがそれは小数点2桁以下を無視しているためであるため、想定通りの処理がコードで実装できていると判断してよいと思います。

ex1.4

次にex1.3までの結果と$\boldsymbol{V}$とのテンソル積を計算してAttenionの出力結果を得る部分の処理を実装します。

# 問題
# 以下の変数ex1_4に計算結果を代入してみてください。
ex1_4=

さっそく回答を紹介します。処理自体はex1.1とほぼ同じなので手を動かしやすかったかもしれません。

ex_1_4 = torch.matmul(ex1_3, v)

最後に、検算をしてみましょう。
$$
\begin{align}
\text{softmax}\left(\frac{\boldsymbol{Q}\boldsymbol{K}^T}{\sqrt{d_k}}\right)\boldsymbol{V}
&= \begin{pmatrix}
0.014 × 9+ 0.98 × 11 & 0.014 × 10 + 0.98 × 12 \\
0.00005 × 9 + 0.99994 × 11 & 0.00005 × 10 + 0.99994 × 12 \
\end{pmatrix} \\
&= \begin{pmatrix}
10.9... & 11.9... \\
10.9... & 11.9... \
\end{pmatrix}
\end{align}
$$
コードの実行結果と同様の結果になったことが確認できました。

ex2 MULTIHEAD ATTENTION

次にex1を応用してバッチ、headがある場合Attention(MULTIHEAD ATTENTION)の実装していきましょう。
以下の、テンソルサイズ[b,h,n,d_k]=[1,2,2,2]のQ,K,Vをインプットの例として結果の確認も行っていきたいと思います。

# tensor shape: [b,h,n,d] = [1,2,2,2]
Q = torch.tensor([[[[1,3],[5,7]],[[2,4],[6,8]]]]).float()
K = torch.tensor([[[[9,11],[13,15]],[[10,12],[14,16]]]]).float()
K = torch.tensor([[[[17,19],[21,23]],[[18,20],[22,24]]]]).float()

ではさっそく実装をしていきましょう。

# 問題　以下のコードを穴埋めし、最終出力結果をex2に代入してください
# QとK^Tの積を計算
dots = 
# スケール処理した後softmaxで処理
scale = 2**-0.5
softmax = 
attn = 
# 最終出力
ex2 = 

さっそく回答を紹介します。

# QとK^Tの積を計算
dots = torch.matmul(Q, K.transpose(-1, -2))
# スケール処理した後softmaxで処理
scale = 2**-0.5
softmax = nn.Softmax(dim=-1)
attn = softmax(ex2_1 * scale)
# 最終出力
ex2 = torch.matmul(ex2_2, V)

では結果の確認をしていきましょう。
ここからは、出力結果のテンソルのサイズが想定通りになっているかを確認していきましょう。
想定としては(1, 2, 2, 2)サイズのテンソルになるはずです。
以下のようにテンソルサイズを出力することで正しいことが確かめられます。

print(ex2.size())
# 出力→torch.Size([1, 2, 2, 2])

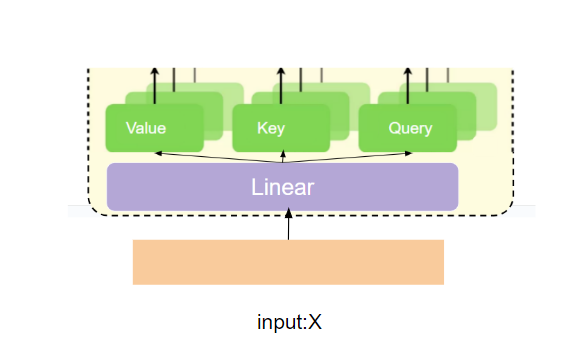
ex3 Q,K,Vの生成

次にQ,K,Vの作る部分の処理を実装していきましょう。

以下の、サイズ(b,n,D)=(2,3,4)のテンソルをインプットの例として結果の確認も行っていきたいと思います。

x = torch.rand(2, 3, 4)

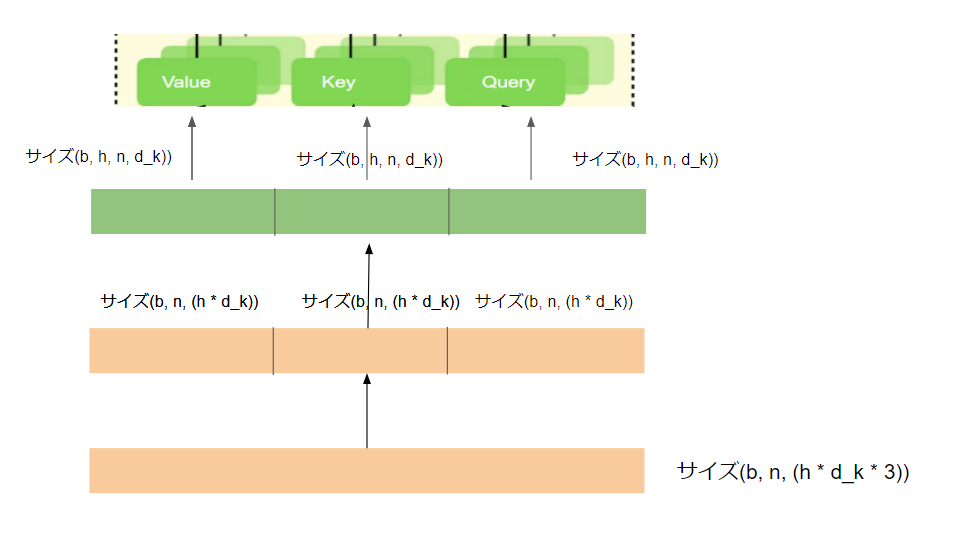
ex3.1

最初に(b, n, D)サイズの入力を(b, n, (h * $d_{k}$ * 3))のサイズの入力に変換する処理を実装します。

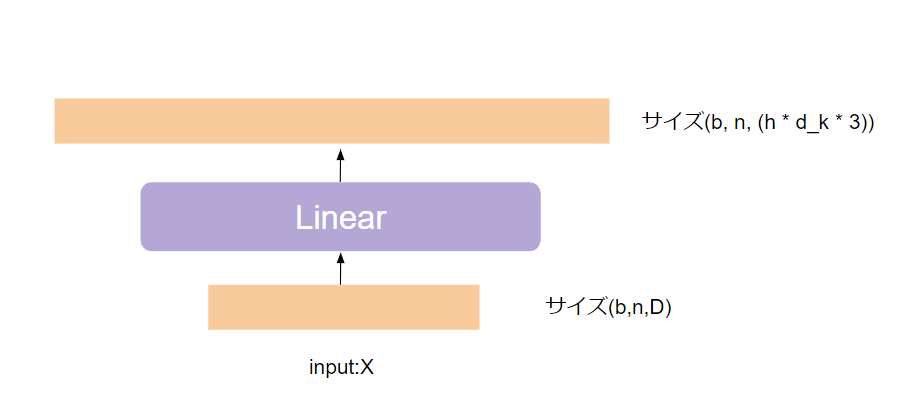
# 問題　以下のコードを穴埋めし、最終出力結果をex3_1に代入してください
d_k = 3
# nn.Linearの引数部分を穴埋めする
to_qkv = nn.Linear()
# 最終出力
ex3_1 = to_qkv(x)

回答はこちらとなります。

# 回答
to_qkv = nn.Linear(D, h * d_k * 3, bias=False)
ex3_1 = to_qkv(x)

テンソルのサイズが想定通り(2, 3, 18)であることを確認してみてください。

ex3.2

続いて、ex3.1の結果に対してテンソルの分解→reshape→テンソルの分割の処理をしてQ,K,Vのテンソルを生成します。

# 以下のコードを穴埋めし、最終出力結果をex3.2に代入してください

# 1つのテンソルを3つのテンソルに分解
# pytorchのchankメソッドを使う
qkv = 
# テンソルを3リサイズし３つの変数に分割
# rearrangeの引数を埋める
q, k, v = map(lambda t: rearrange(), qkv)

回答はこちらになります。

# 回答

# 1つのテンソルを3つのテンソルに分解
qkv = ex3_1.chunk(3, dim=-1)

# テンソルを3リサイズし３つの変数に分割
Q, K, V = map(lambda t: rearrange(t, "b n (h d_k) -> b h n d_k", h=h), qkv)

テンソルのサイズが想定通り(2, 2, 3, 3)であることを確認してみてください。

ex4　Attention出力後の処理

次に、Attention出力後の処理を実装していきます。
Attentionの出力結果(ex2の結果)に対してreshape→テンソルサイズの変換を適用しサイズを(b,h,n,d_k)→(b,n,D)に変換します。

# 問題　以下のコードを穴埋めし、最終出力結果をex4に代入してください
d_k = 4
D = 5
# reshape
# rearrangeの引数を埋める
out = rearrange(ex2_3, )
# テンソルサイズの変換
# nn.Linearの引数を埋める
to_out = nn.Sequential(nn.Linear(), nn.Dropout(dropout))
ex4 = 

回答はこちらになります。

# 回答
out = rearrange(ex2_3, "b h n d -> b n (h d)")
to_out = nn.Sequential(nn.Linear(d_k,D), nn.Dropout(dropout))
ex4 = to_out(out)

テンソルのサイズが想定通り(1, 2, 5)であることを確認してみてください。

ex5　Attentionクラスの実装

最後にこれまでの処理をAttentionという名前のpytorchのクラスとして記述してみましょう。

# 問題以下のコードの穴埋めをしてみてください
class Attention(nn.Module):
    def __init__(self, D, h=8, d_k=64, dropout=0.0):
        super().__init__()
        inner_dim = d_k * h

        self.h = h
        self.scale = d_k**-0.5

        self.attend = nn.Softmax(dim=-1)
        # ex3.1
        self.to_qkv = nn.Linear()
        self.to_out = nn.Sequential(nn.Linear(), nn.Dropout(dropout))

    def forward(self, x):
        # ex3.2
        qkv = 
        Q, K, V = map(lambda t: rearrange(), qkv)
        
        # ex2.1,2.2
        dots = 
        attn = self.attend(dots)
        
        # ex2.3
        out = 
        
        # ex4.1
        out = 
        return 

回答はこちらになります。

# 問題以下のコードの穴埋めをしてみてください
class Attention(nn.Module):
    def __init__(self, D, h=8, d_k=64, dropout=0.0):
        super().__init__()
        inner_dim = d_k * h

        self.h = h
        self.scale = d_k**-0.5
        self.attend = nn.Softmax(dim=-1)
        # ex3.1
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
        self.to_out = nn.Sequential(nn.Linear(inner_dim, D), nn.Dropout(dropout))

    def forward(self, x):
        # ex3.2
        qkv = self.to_qkv(x).chunk(3, dim=-1)
        Q, K, V = map(lambda t: rearrange(t, "b n (h d) -> b h n d", h=self.h), qkv)
        
        # ex2
        dots = torch.matmul(Q, k.transpose(-1, -2)) * self.scale
        attn = self.attend(dots)
        out = torch.matmul(attn, V)
        
        # ex4
        out = rearrange(out, "b h n d -> b n (h d)")
        return self.to_out(out)

確認として、サイズ(64, 65, 1024)のテンソルを処理した時のサイズを確認してみてください。

# 確認
x = torch.rand([64, 65, 1024])
atten = Attention(D=1024, h=8, d_k=64, dropout=0.5)
output = atten(x)
print(output.size())

出力結果がtorch.Size([64, 65, 1024])となっていれば正解です。

最後に

以上でAttetionの実装までできました。１つ１つの処理自体はpytorchで見たことがある機能を組み合わせになっていることがわかるかと思います。ぜひ、pytorchをこれから使っていきたいという方がpytorchに慣れるための題材として本記事が力になれば幸いです。