合計と平均
numpy.sum(data) #合計
numpy.mean(data) #平均
最大値と最小値、及び中央値
numpy.amax(data)
numpy.amin(data)
numpy.median(data)
分散
「データが平均値からどれほど離れているか」を表す指標
\sigma^2=\frac{1}{N}\sum_{i=1}^{n} (x_i-\mu)^2
numpy.var(data, ddof = 0)
不偏分散
標本分散は、標本平均を用いてさらに分散を計算した値だが、この値は、過小に見積もってしまうというバイアスが起こる。
そこでバイアスをなくしたものが普遍分散となる
\sigma^2=\frac{1}{N-1}\sum_{i=1}^{n} (x_i-\mu)^2
numpy.var(data, ddof = 1)
以降、不偏分散を利用する。
標準偏差
分散の平方根をとったもの
\begin{align}
\sigma&=\sqrt{\sigma^2}\\
&=\frac{1}{N-1}\sum_{i=1}^{n} (x_i-μ)^2
\end{align}
numpy.std(data, ddof=1)
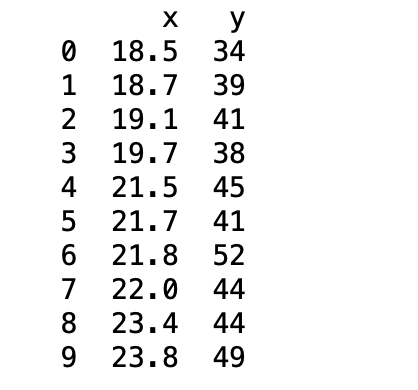
共分散
- 共分散が0よりも大きい時
→片方の変数が大きい値をとれば、もう片方も大きくなる
→正の相関がある。 - 共分散が0よりも小さい時
→片方の変数が大きい値をとれば、もう片方は小さくなる
→負の相関がある。
Cov(x,y)=\frac{1}{N}\sum_{i=1}^{n-1} (x_i-\mu_x)(y_i-\mu_y)
# データの取り出し
x = cov_data["x"]
y = cov_data["y"]
# サンプルサイズ
N = len(cov_data)
# 平均値の計算
mu_x = sp.mean(x)
mu_y = sp.mean(y)
# 共分散
cov = sum((x - mu_x) * (y - mu_y)) / (N - 1)
分散共分散行列
Cov(x,y)=
\begin{bmatrix}
\sigma_x^2 & Cov(x,y) \\
Cov(x,y) & \sigma_y^2
\end{bmatrix}
np.cov(x, y, ddof = 1)
行列から値を取り出す時
hoge = np.cov(x, y, ddof = 1)
cov = hoge[1,0]
ピアソンの積率相関係数
共分散を、最大値1、最小値1に標準化したもの。
\rho_{xy}=\frac{Cov_{(x,y)}}{\sqrt{\sigma_x^2\sigma_y^2}}
# 分散の計算
sigma_2_x_sample = sp.var(x, ddof = 0)
sigma_2_y_sample = sp.var(y, ddof = 0)
# 相関係数
cov_sample / sp.sqrt(sigma_2_x_sample * sigma_2_y_sample)
相関行列
Cov_{(x,y)}=
\begin{bmatrix}
1 & \rho_{xy} \\
\rho_{xy} & 1
\end{bmatrix}
numpy.corrcoef(x,y)
標準化
データの平均を0,標準偏差を1にする変換のこと。すなわち、各データから平均値を引き、標準偏差で割ったもの。
standerd = (data - numpy.mean(data)) / numpy.std(data, ddof=1)
確率密度
連続型変数1における確率のこと。
連続型変数の時、特定の値の確率は常に0となってしまう。というのも、なんらかの値は小数点以下が無限に続いているためである。例えば、人の身長が160センチちょうどということはありえないということである。しかし、「159センチ以上160センチ以下の人の確率」なら求めることができる。その確率のことが「確率密度」である。
e.g. 0から最大値までの確率密度は1となる。
c.f.離散型変数2における確率が多くの人が学校で習う確率のことである。(P(x)=1/4)
特に、実数値をとる変数Xがx<=X<=x+⊿xをとる確率を考える際、⊿x→0の時、P(x)をxの確率密度という。
確率変数
確率を計算する時、計算の対象となる変数を確率変数という。
x=2となる確率が1/3であるとする。このときの2が確立変数である。
正規分布の確率密度関数
N(x|\mu, \sigma^2)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-{\frac{(x-\mu)^2}{2\sigma^2}}}
例:確率変数x=3、平均=4、標準偏差=0.8の時
>>>x = 3
>>>mu = 4
>>>sigma = 0.8
>>>1 / (numpy.sqrt(2 * sp.pi * sigma**2)) * numpy.exp(- ((x - mu)**2) / (2 * sigma**2))
>>>0.228
また、下の関数で簡単にできる。
>>>stats.norm.pdf(loc = 4, scale = 0.8, x = 3)
>>>0.228
累積分布関数と下側確率、パーセント点
F(x)=P(X\leq x)
のように表される関数のこと。
すなわち、「ある値以下となる確率を計算する関数」のこと。
ここで得られた値を下側確率という。また、この時のxをパーセント点という。
正規分布の時は下の積分計算で求められる。
また、scipy.stats.hoge.cdf関数を用いる
P(X\leq x)=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi\sigma^2}}e^{-{\frac{(x-\mu)^2}{2\sigma^2}}}dx
>>>import scipy as sp
>>>from scipy import stats
>>>stats.norm.cdf(loc = 4, scale = 0.8, x = 3) #locは平均、scaleは標準偏差
>>>0.106
パーセント点を求める関数-ppf関数
下側確率が2.5%となるパーセント点
>>>stats.norm.ppf(loc = 4, scale = 0.8, q = 0.025)
>>>2.432
t値とt値の標本分布
t=\frac{\hat{\mu}-\mu}{\frac{\hat{\sigma}}{\sqrt{N}}}
すなわち、
t値=\frac{標本平均-母平均}{標準誤差}
となる。この試行を複数回繰り返したものの分布がt値の標本分布である。
t分布
母集団分布が正規分布である時のt値の標本分布のことをt分布という。
t検定
データの平均値が特定の値と異なるかどうかを調べるもの。
ただ、t検定の具体的な手法はデータの対応関係により変わる。詳細は以下のページを参照のこと。
statsモジュールの関数
ピアソン残差
「普通の残差を分布の標準偏差で割ったもの」と解釈される。
例:二項分布の時
- p=0.5の時は0か1になるが半分であることを表すため、推測が当たる確率も低くなる。この時のズレは、ピアソン残差では「小さなズレ」として認識される。
- p=0.9の時は推測が当たる確率が高いはずである。この時に推測が外れた場合、ピアソン残差では「大きなズレ」として認識される。
\begin{align}
Pearson \quad residuals &= \frac{y-N\hat{p}}{\sqrt{N\hat{p}\quad(1-\hat{p}\quad)}}\\
&=\frac{y-\hat{p}}{\sqrt{\hat{p}\quad(1-\hat{p}\quad)}}
\end{align}
\\
\hat{p}\quadは推測された成功確率を表す。
ピアソン残差の平方和はピアソンカイ二乗統計量となる。